總有人會問說中樂透的機率啦、中發票的機率啦,摸起來就天胡大四喜之類的機率啦等等等等的,這兩篇文章就打算來看看簡單的排列組合跟機率問題,以後遇到就都自己算吧。先從排列開始:
[排列] 有 n 個不同東西排成一列,共有幾種排法?
Ans. n !
大家應該都很熟悉階乘了,不過作為參考這裡還是說明一下。
假設 n 種東西就有 P(n) 種排法,那我們可以隨便挑一種放第一個,總共有 n 種挑法,每當我們決定第一個東西後都剩下 n-1 種東西要繼續排列,也就是有 P(n-1) 種排法,所以 P(n) = n x P(n-1)。而當剩下一種東西時,P(1) = 1:
[組合] 從 m 個不同東西中挑 n 個出來,共有幾種挑法?
Ans. 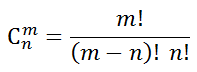
以後看到 C 直接背答案比較快:
上階除以上減下階、下階,至於這個結果也可以從排列得來。
首先我們先把 m 個東西做排列,規定不管怎麼排,前面的 n 個就是我們要的,顯然很多種排列方式對我們而言其實都是同一種挑法。
舉例來說要從 A~E 中挑兩個字母出來,那麼 BE | ACD、EB | DCA、EB | DAC 、 BE | CAD 等等都算是挑出 BE 的一種排列方式而已。
對一種挑法 (組合) 而言,你可以先挑出 n 種,然後把它們亂排列,沒挑到的 m-n 個東西也都亂排,反正都是同一種組合,如此共有 n! x (m-n)! 種排列方式都屬於同一種組合。
問題是總共有幾種組合?阿災,C(m,n) 種;每種組合對應 n! x (m-n)! 種排列方式,所有的排列方式為 m! 種:
移項一下就是答案了。
這裡來做兩個小結:
1. 我們可以注意到組合式中分母的 n! 和 (m-n)! 是可以互換的,那是因為當我們在大樂透中挑 6 個想要的數字時,其實就等於在挑 43 個不想要的數字,所以:
2. 有時候會看到從 m 個東西裡挑出 n 種東西來排列的情況,記成 P(m,n),那就先挑再排就好了: