題目連結:
題目意譯:
你被給定一個 n × n 整數矩陣。你可以做以下操作任意次:
選擇矩陣中任兩個相鄰元素並將兩者之值皆乘以 -1。
兩元素視為相鄰若且唯若它們有著共同的邊界。
你的目標是最大化矩陣的元素總和。回傳上述提及的操作所能得到的最大矩陣元素和。
限制:
n == matrix.length == matrix[i].length
2 ≦ n <= 250
-10 ^ 5 ≦ matrix[i][j] ≦ 10 ^ 5
範例測資:
範例 1:
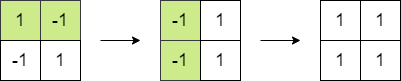
輸入: matrix = [[1,-1],[-1,1]]
輸出: 4
解釋: 我們可以按照以下步驟得到總和值 4:
- 將第一列兩個元素乘以 -1。
- 將第一行兩個元素乘以 -1。
範例 2:
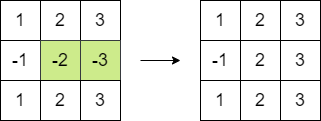
輸入: matrix = [[1,2,3],[-1,-2,-3],[1,2,3]]
輸出: 16
解釋: 我們可以按照以下步驟得到總和值 16:
- 將第二列最後兩個元素乘以 -1。
解題思維:
(雖然 0 本身沒有正負。但是為了方便,以下將 0 視為負數)
可以看到每兩個相鄰元素乘以 -1 只會有以下三種情況發生:
一:兩個都是正的。則整個矩陣將會多出兩個負的元素;
一:兩個都是負的。則整個矩陣將會多出兩個正的元素;
一:一正一負。則整個矩陣正或負之元素數量不變,但是負號會從原本的元素跑到另一個元素上。
因此根據以上情況,我們可以將矩陣中兩個「負號」移動到相鄰位置,此時就可以一口氣將兩個負的元素變為正的元素。
所以假設整個矩陣中有著 X 個負的元素(注意這邊已經將 0 當作負數了),則:
當 X 為偶數時,代表我們可以完全地將負號消除掉。因此此時最大的可能矩陣元素和即為原先每個元素絕對值之和。
當 X 為奇數時,代表我們可以消到剩一個負號,並且可以將該負號移動到絕對值最小的元素上。因此此時最大的可能矩陣元素和即為 (原先每個元素絕對值之和) - 2 × (矩陣中絕對值最小者)。
此次分享到此為止,如有任何更加簡潔的想法或是有說明不清楚之地方,也煩請各位大大撥冗討論。