題目連結:
題目意譯:
你現在在一座城市中,其由 n 個路口編號為 0 到 n - 1 所組成,且其中有些路口之間有著雙向的道路。輸入之生成保證你可以從任意一個路口抵達任何其他路口,而且兩個路口之間最多只會有一條雙向的路。
你被給定一個整數 n 以及一個二維整數陣列 roads 其中 roads[i] = [ui, vi, timei] 代表著在路口 ui 和 vi 之兼有著一條路且要花 timei 分鐘穿越。你想要知道在花費最少時間之下有多少方式可以從路口 0 走到路口 n - 1。
回傳你可以在最短時間內抵達你的目的地的方法數。由於答案可能很大,因此將其模 10 ^ 9 + 7 後回傳。
限制:
1 ≦ n ≦ 200
n - 1 ≦ roads.length ≦ n × (n - 1) ÷ 2
roads[i].length == 3
0 ≦ ui 、 vi ≦ n - 1
1 ≦ timei ≦ 10 ^ 9
ui != vi
任意兩路口之間最多只會有一條路。
你可以從任一路口走到任何其他的路口。
範例測資:
範例 1:
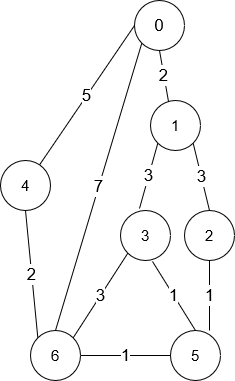
輸入: n = 7, roads = [[0,6,7],[0,1,2],[1,2,3],[1,3,3],[6,3,3],[3,5,1],[6,5,1],[2,5,1],[0,4,5],[4,6,2]]
輸出: 4
解釋: 從路口 0 走到路口 6 最少所需時間為 7 分鐘。
四個你可以在 7 分鐘抵達目的地的方式為:
- 0 ? 6
- 0 ? 4 ? 6
- 0 ? 1 ? 2 ? 5 ? 6
- 0 ? 1 ? 3 ? 5 ? 6
範例 2:
輸入: n = 2, roads = [[1,0,10]]
輸出: 1
解釋: 只有一個方式可以從路口 0 走到路口 1,且需花費 10 分鐘。
解題思維:
基本上就是寫一個單一起點最短路徑(Single-Source Shortest Path)即可,例如戴克斯特拉演算法(Dijkstra's Algorithm,參見
維基的說明)。
此次分享到此為止,如有任何更加簡潔的想法或是有說明不清楚之地方,也煩請各位大大撥冗討論。