題目連結:
題目意譯:
給定一個二元樹的根節點 root����,請藉由刪除其中一條邊來將二元樹分為兩個子樹使得兩子樹各自總和之乘積為最大��。
回傳兩子樹各自總和之乘積的最大值。由於答案可能太大,將其模 10 ^ 9 + 7 後回傳���。
注意你需要最大化的是取模前的答案,不是取模後的。
限制:
樹中的節點數位於範圍 [2, 5 × 10 ^ 4]。
1 ≦ Node.val ≦ 10 ^ 4
範例測資:
範例 1:
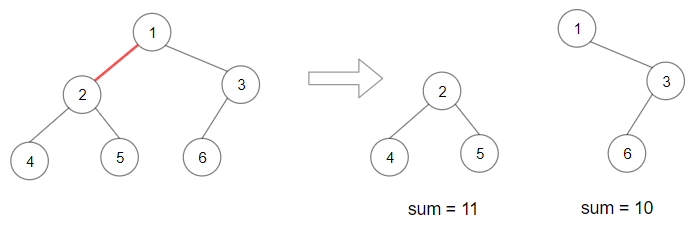
輸入: root = [1,2,3,4,5,6]
輸出: 110
解釋: 移除紅色的邊可得到兩子樹有著總和 11 和 10�����。它們的乘積為 110(11 × 10)��。
範例 2:
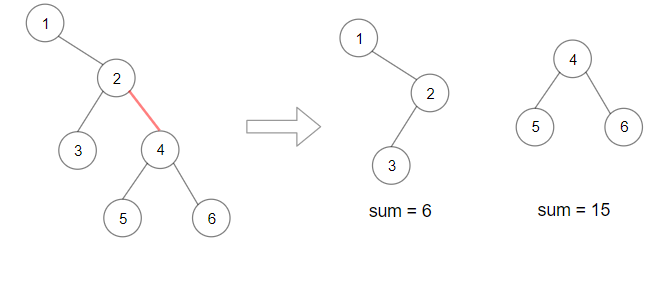
輸入: root = [1,null,2,3,4,null,null,5,6]
輸出: 90
解釋: 移除紅色的邊可得到兩子樹有著總和 15 和 6��。它們的乘積為 90(15 × 6)。
範例 3:
輸入: root = [2,3,9,10,7,8,6,5,4,11,1]
輸出: 1025
範例 4:
輸入: root = [1,1]
輸出: 1
解題思維:
首先,遞迴地將所有樹中的節點值變為其原本節點值加上其兩子樹的節點值總和(如果其中一個子樹不存在則其值為 0)��。假設所有節點值的總和為 T�,可以看到其為 root->val。
接著再遞迴一次,看切掉哪一條邊可以湊得最接近�、但不大於 T ÷ 2 的數值總和值:
如果我們現在在節點 N���,其有左子樹根節點 L �、 右子樹根節點 R�。
當切掉 N 到 L 這條邊會得到兩棵樹。一棵值為 L->val、另一棵為 T - L->val�����。取其中最小�����,稱為 A�。
當切掉 N 到 R 這條邊會得到兩棵樹�����。一棵值為 R->val��、另一棵為 T - R->val。取其中最小�,稱為 B���。
因此我們的目標就是所有 A ���、所有 B 值中最大者�����,該數字即為最接近並小於等於 T ÷ 2 的數字,我們稱其為 X。
因此所求最大乘積值即為 X × (T - X)���,模 10 ^ 9 + 7 後即為所求。
此次分享到此為止,如有任何更加簡潔的想法或是有說明不清楚之地方��,也煩請各位大大撥冗討論����。