題目連結:
題目意譯:
給定一個二元樹 root���,一個樹中的節點 X 會被稱為「好」如果存在一條從 root 到 X 的路徑�����,其中沒有節點有著大於 X 之節點值。
回傳該二元樹的好節點之數量。
限制:
二元樹的節點數量位於範圍 [1, 10 ^ 5]。
每個節點值介於 [-10 ^ 4, 10 ^ 4] 之間��。
範例測資:
範例 1:
輸入: root = [3,1,4,3,null,1,5]
輸出: 4
解釋: 標以藍色的節點是好的�����。
根節點(3)永遠是一個好節點��。
節點 4 → (3, 4) 為從 root 開始的路徑上之最大值。
節點 5 → (3, 4, 5) 為從 root 開始的路徑上之最大值。
節點 3 → (3, 1, 3) 為從 root 開始的路徑上之最大值��。
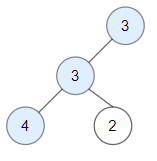
範例 2:
輸入: root = [3,3,null,4,2]
輸出: 3
解釋: 節點 2 → (3, 3, 2) 不好�,因為 "3" 大於它。
範例 3:
輸入: root = [1]
輸出: 1
解釋: 根節點被視為是好的。
解題思維:
因為給定的是一棵樹���,因此從根節點開始到任一節點結束也只會有唯一一條路徑。
因此我們只需採取深度優先搜尋(Depth First Search,DFS)的策略從根節點走到所有節點,期間維護著當前路徑上的最大值為何。當新遇到的節點是整個路徑的最大值,就代表該節點是好的。
因此 DFS 探訪結束後�,過程中遇到的好節點數量即為所求�。
此次分享到此為止�,如有任何更加簡潔的想法或是有說明不清楚之地方,也煩請各位大大撥冗討論。