題目連結:
題目意譯:
現有一個索引值從 1 開始的二元矩陣,其中 0 代表著陸地、1 代表著水。你被給定整數 row 和 col 依序代表著矩陣的列數以及行數。
一開始在第 0 天,整個矩陣為陸地。但是,每一天會有一格將充斥著水。你被給定一個索引值從 1 開始的二維陣列 cells,其中 cells[i] = [ri, ci] 代表著第 i 天時,位於第 ri 列第 ci 行(座標值從 1 開始數)的那個格子將被水覆蓋(即變成 1)。
你想要找到可以只經由陸地格子從最上面走到最下面的最後一天為何。你可以從最上面一列的任意一個格子開始走到最後一列的任意一個格子。你只可以四種基本方向(上下左右)行進。
回傳可以只經由陸地格子從最上面走到最下面的最後一天之天數。
限制:
2 ≦ row 、 col ≦ 2 × 10 ^ 4
4 ≦ row × col ≦ 2 × 10 ^ 4
cells.length == row × col
1 ≦ ri ≦ row
1 ≦ ci ≦ col
所有 cells 之值彼此相異。
範例測資:
範例 1:
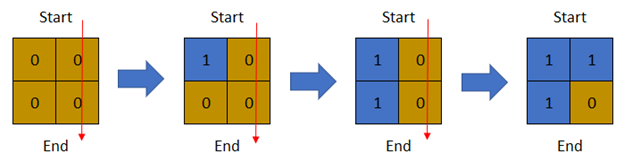
輸入: row = 2, col = 2, cells = [[1,1],[2,1],[1,2],[2,2]]
輸出: 2
解釋: 上圖顯示了矩陣從第 0 天開始的變化。
可以從最上面走到最下面的最後一天之天數為 2。
範例 2:
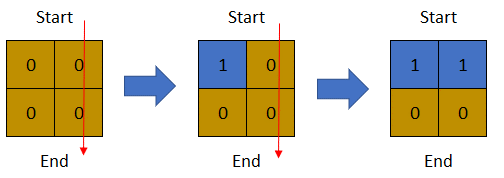
輸入: row = 2, col = 2, cells = [[1,1],[1,2],[2,1],[2,2]]
輸出: 1
解釋: 上圖顯示了矩陣從第 0 天開始的變化。
可以從最上面走到最下面的最後一天之天數為 1。
範例 3:
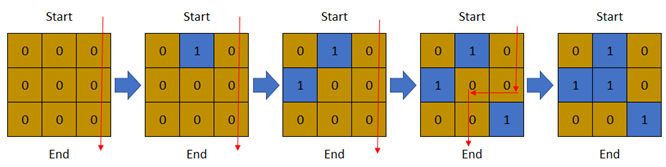
輸入: row = 3, col = 3, cells = [[1,2],[2,1],[3,3],[2,2],[1,1],[1,3],[2,3],[3,2],[3,1]]
輸出: 3
解釋: 上圖顯示了矩陣從第 0 天開始的變化。
可以從最上面走到最下面的最後一天之天數為 3。
解題思維:
一個較為單純的作法為對答案進行二分搜尋法(Binary Search),如
這題。因為如果我們最後一天能通過的天數為第 i 天,則代表著第 0 ~ i 天都可以通過,在此之後的任何一天則不行。因此才可以對著天數進行二分搜。
而檢查某一天可不可行從頂端到底部也不難,只要先把 cells[0] ~ cells[i - 1] 每一個格子填滿水(也就是 1),剩下格子為陸地(也就是 0)。接著利用廣度優先搜尋(Breadth First Search,BFS)從頂端開始擴張,看是否可以抵達底部。
因此總體時間複雜度為 O(n log n),其中 n = row × col。
利用一個併查集(Union-Find Set)來把所有是陸地的格子連在一起。
(請忽視題目提及陣列 cells 索引值從 1 開始這件事,這邊是從 0 開始,也就是按照「大部分」程式語言的邏輯)
我們從 cells 的尾端開始掃到開頭,因此一開始所有格子都是水。接著每次加入 cells[i] 這個格子作為陸地(這個動作形同「復原」,把原本是水的格子還原成陸地)。然後檢查第一列在併查集中的 parent 是否與最後一列相同。如果相同則代表頂端與底部互通。則代表正因為第 i 天「後」cells[i] 所代表的格子變成了水所以才無法通行,因此最後一天可從最上面走到最下面即為第 i 天。
不過因為一般的併查集使用的索引值是單一值,而我們的格子位於二維平面上,所以是雙重的索引值 (r, c)。不過這問題很好解決,我們只需要 (r, c) 套入
(r × (col + 2) + c)
便可以變成一個單一數值。而因為每一次加入一個陸地格子,我們有機會會把其上下左右的格子連在一起。而為了不做額外的邊界判斷,所以上式多了一個 「+ 2」(可以視為第 0 行和第 col + 1 行)。同時在最上、最下多加兩列(第 0 列以及第 row + 1 列)陸地,最上面那一列所有人的 parent 為 (0, 1)、最下面那一列所有人的 parent 為 (row + 1, 1)。而這也是為了不做邊界檢查之緣故,且檢查連通性將變得更容易(只要檢查 (0, 1) 和 (row + 1, 1) 的 parent 相不相同即可)。
此次分享到此為止,如有任何更加簡潔的想法或是有說明不清楚之地方,也煩請各位大大撥冗討論。