數學心得:314 國際數學日 圓周率日
昨日3/14,可是重要的一天,用偉大的無理數 圓周率 pi 所命名的 國際數學日 也稱圓周率日
在此紀錄感動與數學心得
當然要來宣傳一下 後天 3/16 -17在科教館 有 數學日的活動
更可以來看看國際的官網:國際數學日快樂!
中華民國數學會、國立臺灣科學教育館將於 3/16-17 兩天在臺北市士林科教館共同舉辦 2024 年《國際數學日》慶祝活動,目標是通過這一天,向大眾展示數學的重要性,讓大家更加了解數學在各個領域的應用。我們希望透過相關活動,讓學生、教師、女性以及整個社會都能受益。
我應該沒空去就是了...
懷念幾年前有去現場,真的很有趣
可以看看這篇文:3/14 國際數學日—遊記心得
三年前的心得就是
大推此活動,絕對是寓教於樂的數學活動,數學絕不是只是考試用的科目而已!
還有的「數學詠唱者」AI 生成式藝術圖像,得獎作品超漂亮
今年的主題是 #遊於數 (Playing with Math),海報設計更藏了巧思,裡面有六個有趣的遊戲!快來參加吧!挑戰一下自己的數學解題技能,在3月14日當天公佈正確答案哦!
2024海報謎題挑戰
就是此海報上的六個謎題
有趣的是,本張海報完全沒有說這些謎題要怎麼玩,要自己發現這些到底是怎麼玩的!
這就是考驗數學素養、數學能力的時候了!
答案在這邊 建議自己想想再來看
3/14晚上的課,很巧,我跟厲害又喜愛數學的學生講述今天是圓周率日
也將上面的謎題當作給學生的發揮,更看看能否體會出這些謎題想要解什麼
我相信對數學有點興趣的人
應該是多少能領會這其中的謎題
這邊用放大的圖來解說,有些我就用對話的形式來解說
1.
「這就是數獨吧」
「沒錯,左邊紫色的是正是提示」
所以可以很快地解出
2.
「一筆畫畫完?」
「畫完什麼?」
「所有的路徑? 不對,是點才對,線沒有連完沒關係」
「沒錯,還要注意這要回到原點,這可是在圖論著名的漢米爾頓路徑問題,此圖就是最有名的正十二面體的圖」
學生領悟力與觀察力很高,三兩下便可意會上圖的提示究竟想要做什麼
我也介紹起漢米爾頓圖形
在圖形上,經過所有的點且不重複點而回到原來的出發點,這樣的問題我們稱之為“漢米爾頓迴路(Hamilton cycle)"此情況是迴路,若不走回原點,叫做漢米爾頓路徑(Hamilton path)
而這個圖很經典,因為是將立體的正十二面體,做成平面的樣子,這樣可以發現,確實存在一個路徑可以回到原點,而且走完全部的點,代表在立體三維的情況下也可以做到這件事。將三維的問題轉化成二維的問題,這很有意思吧
3.
這大概是最簡單的一個
藉由上面兩個天秤,要來判斷第三個天秤的情況
也是在問號處填入大於、等於、小於
(其實就是標準的國中課內比例問題)
轉化成數學式子:不妨設 藍色為x、紅色為y、紫色為z,
有條件:4x=5y 、x+2y=2z
判斷:2z+3y 與 4x+y 的大小關係
2z+3y=x+5y=5x > 4x+y
等價於 x > y
4.
這應該很明顯,就是在8之間填入運算符號讓等式成立的遊戲吧
「那就是這樣吧 888+88+8+8+8=1000 成功了」
「也太快,怎麼想的!?」
「因為我看過類似的,一個靈感來就解出來了」
才一眨眼的功夫,便秒殺這題,我不禁佩服學生那敏捷的思考...
另外我原本自己想的是 [(8+8)*8-(8+8+8)/8]*8=1000
這才是我覺得最美的,單純用8個8搭配運算做出來的
另外我也找到:(8+8)*8*8-(88-8*8)=1000
大家可以自己找看看有無其他做法
5.
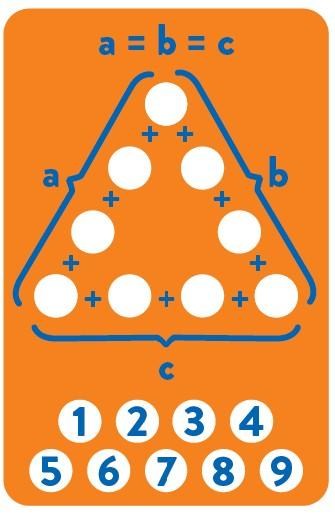
這個應該也很明顯,就是數字陣的問題
提示也蠻清楚的:在空格處填入1-9,每一邊四個數字之和都要一樣
學生當然三兩下便解決
不過要注意,這題有許多種解法,不唯一的
此為其中一種解法
關鍵就是把重複計算的數字(中間數) 找出來看有什麼條件,進而求解
大家也不妨試試看還有什麼解
6.
「最後這個我覺得最難,我猜應該是要利用數字和右邊的圓圈的關係,去破解最後右邊的三綠圓所對應的數字是多少,但我目前沒什麼想法,看不太出來是要有什麼關聯或是關鍵是什麼... 有什麼想法都跟我說吧」
我坦白我沒什麼想法,也期望學生會不會有什麼想法
506 和 791 都是一個黃色底加黑色圈,這兩數會有什麼共通點嗎? 我覺得可以朝這方面想想
一個奇數、一個偶數...不能單看奇偶,但都是在mod3下同餘2,可是314也是同餘2,這說不通...
還要注意749 居然顯示 "–",以及圓的數量又代表什麼?
而最後三個綠圈卻可以顯示唯一的數字,到底是怎樣... 但我猜這應該不會太難才對
就在我苦惱想想這到底暗藏什麼玄機之時,想著是不是什麼同餘、因數個數或其他的數論關係之時...
「會不會這就是1A2B的遊戲啊?黃色代表的是B,綠色應該是代表A,749 顯示 "–"代表什麼都沒有」
「所以最後的答案就是163!」
「真的耶,這合理,你好強!」我馬上進行驗算,發覺完全沒錯,跟學生說的一樣。
而且這符合簡單的要素,我一開始想太難了,這是一般人也能做的趣味數學,怎麼可能扯到質因數分解、數論有得沒得...
我頓時豁然開朗,沒錯就這麼簡單,我怎麼想複雜了呢?我發自內心的感嘆,這位學生真心喜愛數學,又很有才能,在剛剛那瞬間有種被超越的感覺,但我感到興奮與雀躍,這位學生是特別的,跟一般愚蠢的大眾凡夫可不一樣。我希望盡我所能輔佐他。如果能成為數學高手、數學家那我十分樂見。
1A2B 玩法:
一個人設定一組四碼的數字作為謎底,另一方猜。每猜一個數,出數者就要根據這個數字給出提示,提示以XAYB形式呈現,直到猜中為止。其中X表示位置正確的數的個數,而Y表示數字正確而位置不對的數的個數。
(此題就是三個數字的玩法)
就這樣我們把此謎題都解完了,開始看其他難題...
不覺得很美妙嗎?這張海報滿滿的趣味數學~
明明沒有用文字具體寫上如何解這些謎題,但是人們卻能夠靠著對數學的感覺與敏銳度去了解這些謎題究竟要做什麼,我感覺這就是用數學語言溝通的方法...要說暗號也行
有人說,題目在哪裡?只給這種圖要怎麼解啊?
但我覺得這圖幾乎就充分說明了該如何遊戲這些謎題。
就算不用明說,彼此也能夠領會,更別說還有知名的數獨、天秤問題、數字陣
就算一眼無法懂,試圖了解這個謎題的過程也是思考的一環。
數學超越了時間空間。這至高的語言,人們能夠理解並使用數學語言,不覺得太美妙了嗎?
藉著數學能力,可以洞察出題的心思與巧思,無非是數學素養的展現
比什麼為考而考的應用問題好多了
而如果數學差的人,可能沒有感覺這些謎題要做什麼吧。
還有一點值得誇讚,每一題都是一般大眾都有能力解決的!都是簡單的離散數學小遊戲
有哪一題要用到什麼高深的知識嗎?
但有無辦法看到謎題是玩什麼就是厲害之處了
目標是通過這一天,向大眾展示數學的重要性
(不過我更想說,不用這一天,也該展現數學的重要性)
另外來分享一下其他數學日的活動吧
全書都是印滿滿圓周率的一本書,現在三本只要314元!
雖然我有一本了,但還是決定趁這個機會再多買,當作送禮一定很不錯
說來這個暗黑通信團,真的很有意思,專出這種特別的書
晚上下課,看到LINE上的訊息:
「今天國際數學日快樂! 絕對不是情人節快樂喔!」
頓時感到欣慰,居然有人這樣跟我說,我太感動了
其實情人節根本不重要,數學日才是重點!
那晚我感到興奮與快樂
教導那厲害的學生那所感受到的震撼、跟強者的交手、與所愛數學之人的交流、有人願意跟我分享數學學習的心得...這絕不是其他可以比擬的!
當然我也必須持續精進自我的數學才對,別人在變強,我也要變強
我絕對不要當那種一畢業就不讀數學、不精進自我的人,就像某些老師在學校安逸已久,但他們除了課內的東西外,還有再持續學習數學嗎?除了解課內的問題,大學的高等數學是不是都忘了?
微積分基本定理還記得?高等微積分的理論呢?代數學的群環體能夠舉例出來?機率學的各種主要分佈都還清楚?
...
如果忘了,那就多讀,就像大學要當人,自我審核沒過就該重讀,好數學值得一讀再讀。
期望能像某些大學數學教授那樣,如此熟練數學的各種觀念與定理,就算無書無筆記,面對各種數學問題都可侃侃而談。
如果一位數學教師只能會課本的東西,那也不用期望數學能多進步了。
最後在分享一下:
《按圖索驥—無字證明》 這本書,都是用圖形去證明中學的各種數學定理
一種視覺化的方式看待數學證明,當然還是會有一些文字說明
比起代數,有實用圖像化的方式學習更能夠有所感覺
好比下面這個:四大平均不等式
除了常見的算幾不等式,還加上方均根、調和平均數!
讓大家自由領會
數學果然很有趣吧