這裡亞夜。
上禮拜三颱風假,
所以今天沒有仕事日常更新。
剛好前兩天有收到留言,
針對敝人《【日常】數獨解法2》文章的質疑,
既然溝通無果,
那麼乾脆就來發一篇文直接把話講清楚,
免得一直鬼打牆影響心情。
今天要講的東西叫做「唯一性」,
這個並不是在說數獨的基本原則:所有的行、列、宮中都不得出現重複數字,
而是指,
這個數獨的解只有一個且唯一。
換句話說,
這句話等效於「所有的格子都只有一個合法的數字可以填入」。
八年前敝人的這一篇就好巧不巧遇到了重解的題目,
這就是違反了唯一性原則。
唯一性嚴格說起來並不是數獨的必要條件,
只是數獨發展至今,
唯一性被認為是數獨遊戲的默契,
簡單說就是一種潛規則。
為什麼呢?
因為如果重解是被允許的,
那麼極端一點,
81 個格子全部空格也能當作一題不是嗎?
那麼這還叫遊戲嗎?
所以說,
唯一解雖然不是數獨題目的必要條件,
但因為成為了數獨界的默契,
因此我們也可以把這個性質加入到數獨的求解技巧之中。
【基本概念】
首先我們要有的基本概念是,
數獨本身是可以旋轉的。
一個合法的數獨矩陣,
你把他任意旋轉,
或者以宮為單位任意兩行或兩列互換,
或者以行或列為單位,
在同一宮裡面任意兩行或兩列互換,
結果都是合法的。
說到底,
數獨裡的1~9數字其實就只是九種不同的符號而已,
今天你要怎麼改他,
合法的就會是合法的。
【唯一性矩形】
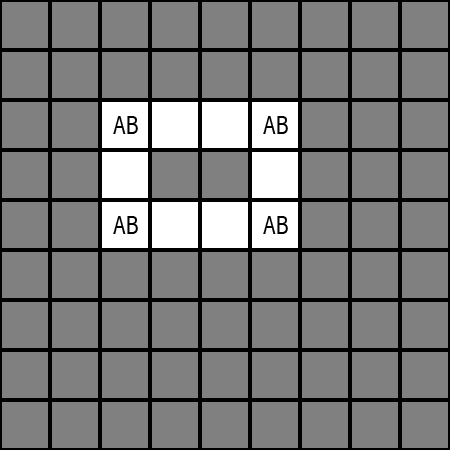
如上面這個範例,
在其他所有格子都已經確定,
只剩下圖中的四個格子剛好都出現 AB 兩組候選數的情況,
那麼很顯然的,
這個題目必然重解。
換句話說,
如果按照唯一性這個潛規則,
那麼這個情況就必然不能發生。
到這裡首先有一個問題:
敝人說其他格子都合法的情況下只剩這四個格子,
但很顯然,
範例中的這四個格子分別位於四個不同的宮,
換句話說這種情況你只需要觀察宮裡的其他數字就能確定其答案,
因此這種情況實際上根本不會發生。
沒錯,
在所有其他格子都確定的情況下,
此情況不會發生。
因此在許多入門教學上都會講:唯一性矩形的四個角落不能位於四個不同的宮。
但實際解題時其實你不需要管他是不是真的沒有位於四個宮,
因為大多數情況下你不會解到最後一步才撞牆,
在過程中,
還有很多未知數尚未確定的情況下,
這種情況一旦出現,
通常就代表哪裡出錯了。
如果沒有錯,
我們實際上會遇到的是這種情況:
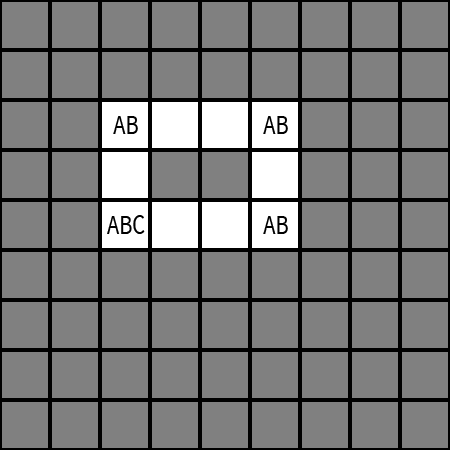
這當然不可能是最終盤面,
不過一旦出現這個盤面,
就可以直接確定 ABC 的那格答案一定不是 AB。
因為不論那格是 A 還是 B,
都會遇到開頭說的那種情況,
也就是所謂的重解。
這裡有一個看起來很像是循環論證的地方:
如果那格是 A 或是 B 則題目出現重解,
意思看起來很像是說這個題目會存在多重解答。
但其實這是不對的。
看起來出現重解,
實際上就是無解。
因為我們一開始已經講了,
這題目具有唯一性是先決條件,
因此不是會出現重解,
而是指會出現「重解的特徵」,
實際上如果這題目具有唯一性,
就代表這個格子只能填入唯一數字,
換句話說,
出現這個特徵就代表填錯,
既然填錯那麼推導到最後並不會出現重解而是直接出現矛盾,
因此就沒有必要思考所謂的「如果」,
你直接可以把該格子的候選數 AB 都消去。
如果剩下來的 C 是唯一候選數,
那麼出數就必然是它了。
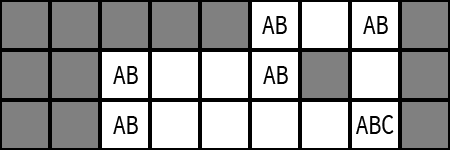
這是一個經典變體,
如果唯一有 C 的那一格是 A 或者 B,
你會發現都能解出合法的解出來,
因此那一格必然不是 A 或者 B。
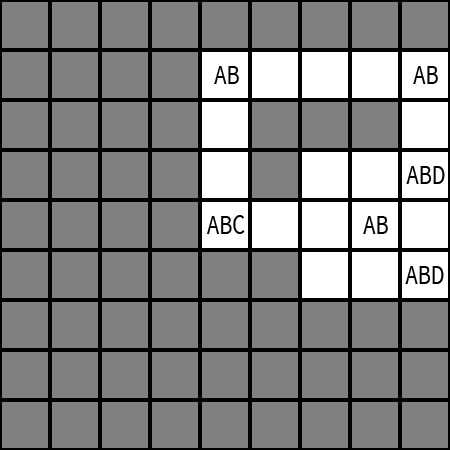
回到敝人之前解題過程中遇到的變體。
這個變體比較誇張,
左下角有候選數 C,
右下角則已經是已知數了。
原則上,
唯一性矩形的應用必須四個角都是未知數,
所以乍看之下這個結構不能直接適用;
但其實結果一樣,
不論如何,
左下角必然不可能是 A 或 B。
很好理解的,
你唯一性矩形任何一個角的出數,
都只會受到相鄰兩個角的影響。
所以同理,
左下角的決定,
只會受到左上角跟右下角的影響。
然而這個構造很奇怪,
右下角的 AB 跟右上角的 AB 錯開,
這不就完全不相關了嗎?
非也,
因為右下角的 AB 同一宮中還有兩個 ABD 存在,
而這個 ABD 必然受到右上角 AB 的牽制。
由於右上角必然得出 AB 其中一個,
因此右下角的兩個 ABD 必然是缺 A 或 B,
所以可以肯定,
右下角的 AB 出數會跟右上角的 AB 出數相同。
而又可以肯定的是,
左上角的 AB 出數必然跟右上角的 AB 出數不同,
換句話說,
左上角的 AB 出數必然跟右下角的 AB 出數不同,
進而導致左下角必然可以消去 AB,
所以左下角的出數必然是 C。
【鬧場的人怎麼說】

這個敝人的原話是:
以這題的場合,
AB分別是49而C是左下角那格的6,
因此左下角那格必然填6。
AB分別是49而C是左下角那格的6,
因此左下角那格必然填6。
我們這裡只定義AB=49,
但A是4還是9都無所謂,
我們只需要確定左下不可以是A或B而必須是C即可。
但A是4還是9都無所謂,
我們只需要確定左下不可以是A或B而必須是C即可。
於是這位「同好」說實際以 A=4 跟 A=9 帶入後得到的 C 值不同,
甚至還附上圖解:
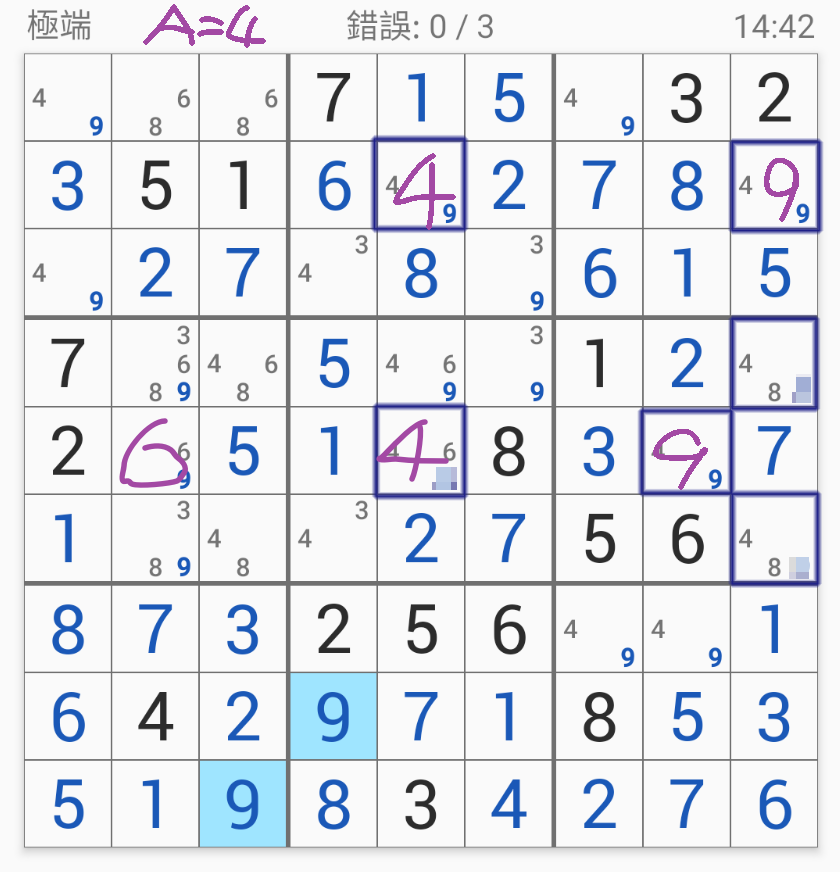
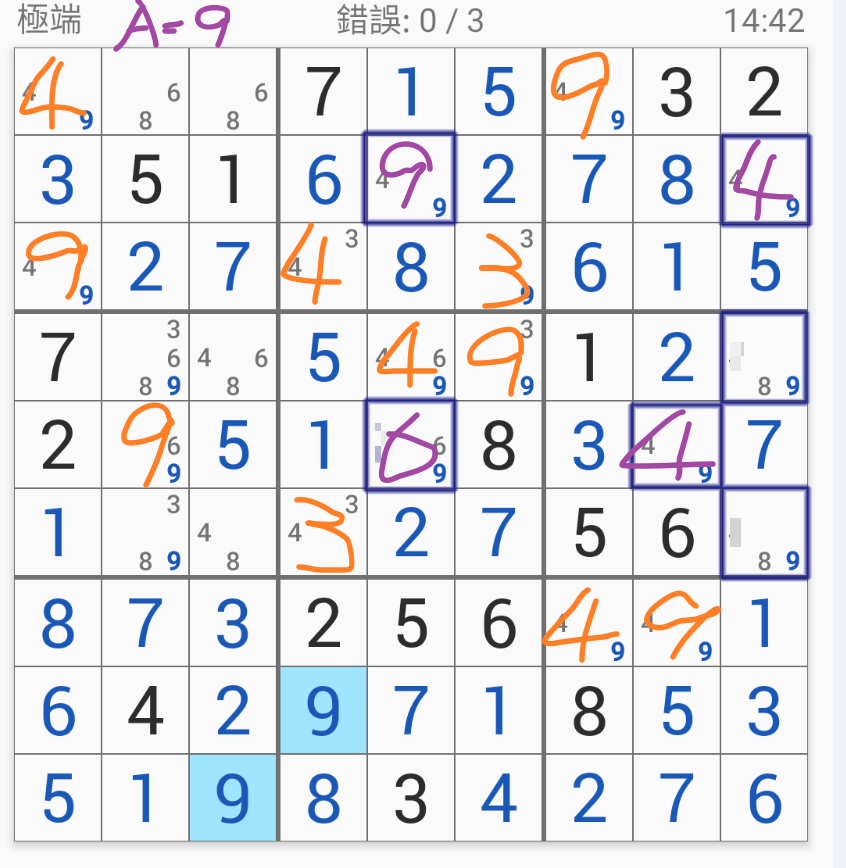
然後說 A=9 帶入後沒問題但 A=4 帶入後出數不同因此結論不對,
但這裡很明顯的矛盾就是,
如果左上是 4,
那左下怎麼也會是 4?
其實到這個階段,
敝人還不認為這位同好是來亂的。
其實從附圖中,
很容易可以得出他的思路:
如果 R2C5(左上角)是 4,
那麼 R2C9(右上角)是 9。
那麼 R4C9 與 R6C9 都能排除 9 形成 48 數對,
因此確定消除 R5C8 的候選數 4 因而確定是 9。
因為 R5C8 是 9 所以 R5C2(候選數 69)的出數是 6,
因為 R5C2 是 6 且 R5C8 是 9 所以 R5C5(左下角)只能是 4。
這位同好的邏輯是正確的,
但是他多走了一步,
就是他多考慮的 R5C2。
這點敝人在給他的回應中已經明確提到,
舉例只是為了說明,
但既然是唯一解的題目,
兩個例子都帶進去驗證必然有一個是錯誤答案,
既然帶到了錯誤答案就必然出現矛盾,
只是你要把矛盾放在哪裡而已。
很好理解,
當 A=4 的這個答案帶進去時是錯誤答案,
所以必然出現矛盾。
而敝人又說不論 A=4 還是 A=9,
左下角的出數都必然是 C=6。
到此就不難理解這位同好的目的:
他就只是想要反駁這一點而已。
【癥結點】

再回頭看這個題目,
剛才我們已經得出結論,
左上角跟右下角的出數必然不同,
這句話等同於左上出 A 右下就出 B;
反之左上出 B 右下就出 A。
因此不論如何,
左下都不可以是 A 或 B,
因此左下必然是 C。
現在我們實際帶入數字,
整個命題是不是就變成:
左上出 4 右下就出 9;


反之左上出 9 右下就出 4。
因此不論如何,
左下都不可以是 4 或 9,
因此左下必然是 6。
這個敝人的原話是:
以這題的場合,
AB分別是49而C是左下角那格的6,
因此左下角那格必然填6。
AB分別是49而C是左下角那格的6,
因此左下角那格必然填6。
我們這裡只定義AB=49,
但A是4還是9都無所謂,
我們只需要確定左下不可以是A或B而必須是C即可。
但A是4還是9都無所謂,
我們只需要確定左下不可以是A或B而必須是C即可。
請問,
原話跟上述的結論是不是等價?
應該是等價的吧!
那為什麼同好帶入後會得出左下出 4 而不是出 6 的情況?
癥結點就出在他多考慮了一步 R5C2,
因為受了 R5C2 的影響而導致 R5C5(左下角)出現不一樣的數字。
【解讀】
請問敝人要怎麼解讀他的訊息?
在敝人完整說明整個癥結點以後,
他始終抓著「你看我帶A=4就得不出C=6的答案啊,所以你錯」這點,
但為什麼這點令人生氣?
敝人為什麼要說明不論 A 帶入 4 還是 9 都無所謂?
因為只考慮這個結構的場合,
我們能得到左下角必然是 C=6 的結論。
敝人本篇的解題過程也是建立在確定 R5C5=6 以後才能順利往下解下去,
因此確定 R5C5=6 是解這一題的關鍵一手。
那為什麼他帶入 A=4 會出錯?
誠如敝人前面說的,
因為是唯一解的題目,
所以只要你其中一格填錯,
那麼必然會得出矛盾的結果,
否則就叫重解了不是嗎?
因為事後證實左上角必須填入 9,
因此填入 4 的場合必然出現矛盾。
出現矛盾的場合,
就看你怎麼推導,
來讓矛盾出現在哪裡而已。
由於敝人只考慮結構的部分,
所以可以得出不論 A=4 或 A=9 都能確定 C=6 是正解,
言下之意是至於 A=4 還是 A=9 需要另外透過之後的手段來確定。
他老兄帶入了 A=4 之後直接發現矛盾,
於是故意繞了一圈來說左下角必須出 4 而不是 6,
並且在講開了以後還繼續揪著這一點不放,
當然敝人就會認為你老兄就是來鬧場而根本不打算聽人講話。
畢竟你帶入錯誤的數值必然出現矛盾,
既然出現矛盾那當然你愛讓矛盾出哪就出哪,
你可以考慮 R5C2 讓 R5C5 出 4,
實際上就是 R5C5 無解因為跟 R2C5 矛盾;
同理如果照敝人的讓 R5C5 出 6 雖然符合結構,
但直接導致 R5C2 無解,
最終而言還是矛盾。
【到底該不該考慮 R5C2?忽略 R5C2 是合理的嗎?】
為了向鬧場仔解釋為什麼它會得到奇怪的結論,
敝人就跟上面解釋的一樣,
他多考慮了一步 R5C2 因此得到不一樣的結果,
但矛盾就是矛盾,
你帶入了錯誤的數字當然會出現矛盾,
差別在於你想讓矛盾出現在哪而已。
在討論數獨的高階解題技巧的時候,
所謂高階技巧,
指的就是你無法只使用數獨的基本規則,
也就是一個未知的格子裡面把相關的行列宮中已經出現過的數字通通排除的方法來確定答案。
換句話說就是,
這時所有的未知格子都還是剩下複數個候選數,
而你已經無法透過排除行列宮的方式確定候選數,
而必須使用其他額外的方法來確定候選數。
事實上,
敝人八年前《【教學?】數獨解法》介紹的方法 1~7 就是完全的數獨基本規則,
沒有任何一個稱得上高階技巧。
而這個題目中敝人所使用的「唯一性矩形」就是高階技巧的一種。
所有的高階技巧都有一個共通點就是:
他們一定滿足特定的結構,
而這個結構在滿足唯一性原則下必然只會有一個結果,
這個結果就能給我們帶來額外的條件來排除掉候選數。
這也是為什麼敝人會說看到這個結構直接說左下角一定是 C,
因為這已經是經過無數次驗證的經驗總結。
而敝人沒想到的是,
真的有人帶數字進去而不是靠嚴謹的邏輯來推理答案。
這裡出現兩個問題:
一個是敝人的而一個是鬧場仔的。
敝人的問題是直接帶數字求解就不叫解題了而是瞎猜,
反正找一格只有兩個候選數的,
猜對直接解開;
猜錯撞到矛盾以後直接倒退回來然後把候選數刪掉就好,
這根本不叫推理嘛。
而鬧場仔則認為:
解數獨哪有一次只考慮一部份的?當然要全盤考慮啊。
為什麼敝人會忽略 R5C2?
看起來根本就是為了讓 R5C5=6 而故意編織過的謊話嘛!
非也。
敝人解釋一下為什麼可以忽略。
我們現在既然在解結構,
那麼我們當然就要針對結構中彼此互有影響的部份來進行拆解。
其他不影響的部分不消說,
有些結構外的部分可能會對我們要拆解的位置仍有所影響,
但其實那並不重要,
因為我們的目的是要找出正確的出數,
如果我們能夠確定出數正確,
那麼你根本不需要考慮其他會影響的部分,
因為既然出數正確就必然不會矛盾,
所以考慮 R5C2 在這個題目來說根本就是偽命題。
也因此,
敝人才會對鬧場仔故意帶入 A=4 並且得出 R5C5=4 這個白癡結果感到感冒,
因為很顯然就是完全沒把敝人解釋半天的脈絡搞清楚,
只就字面上的「不管 49 結論都一樣」因此「那就帶帶看啊」去處理。
廢話,
你帶數字進去必然有一組會是錯誤的,
錯誤解當然會出現矛盾,
你只要故意讓矛盾出現在 R5C5 不就好了?
說穿了就是在偷換概念。
上面解題的過程中提到,
R2C5 跟 R5C8 的出數不同因此 R5C5 必然只能是 C,
這是最強力的結論。
而鬧場仔單純故意繞一個彎讓 R5C5 出現 C 以外的答案,
無所不用其極,
所以很遺憾的,
鬧場仔認定。
鬧場仔最後還說:
A 是不是等於 4 只要丟計算機跑一下就好。

天兵。
都丟計算機了還玩什麼數獨?
【補充:所以該不該帶入數值】
站在敝人的立場,
玩數獨你不應該在尋找候選數時採取帶入法,
也就是俗稱的「試誤法」。
試誤法顧名思義就是指,
當你不知道該如何消去候選數時,
直接隨便填入一個數字然後再靠著基本規則下去填。
如果你猜對當然就不會出現矛盾,
沒有矛盾當然就算成功解題;
反之出現矛盾就代表猜錯,
既然猜錯那就代表答案是另一個候選數,
但這還叫推理嗎?
別忘了數獨可是邏輯推理的遊戲。
但是在解題過程中,
總是會遇到那種「不管哪個是哪個,反正一定不是那個」的情況。
以這題來說,
AB=49 是已知,
至於哪一個是 4 哪一個是 9 則是未知,
這時我們不能真的帶 4 還是帶 9 進去,
因為這樣會變成上面所說的試誤法。
但是當敝人在解釋結構時,
也只能說是兩個關鍵點的出數必定不同,
所以得出目標點必須是 C 的結論。
但要驗證這個結論不就是直接帶一次進去嗎?
就像你解方程式要確認答案對錯與否不就是直接帶結果進去嗎?
我們現在只是要驗證結構,
當然是就結構已知的部分進行驗證。
當你推到結構外以後,
這不就變成試誤法了嗎?
【結論】
惹敝人不開心? 只是觀點不同而已就想辦法解決問題就好了.唉...這樣就要請人離開 :(
你要不要看看你在說什麼?
觀點不同?
直接扭曲別人的解題過程然後說你有瑕疵你有問題,
這叫觀點不同?
鬧場仔不請你離開,
難道留下來跟你輸贏嗎?
特別發一篇文章出來針對個人,
不好意思,
敝人是真的被氣到了。
跟鬼打牆的人溝通真的很困難,
尤其是對方完全不聽你說話的時候。
人與人之間的尊重呢?

封面圖片:AI生成

