淺談「三垂線定理」,以其細節「逆畢氏定理」
本文章要談的是三垂線定理以及背後會用到的逆畢氏定理,這兩個比較邊緣的定理
多為幾何的部分,需要空間像想像力,可能有點枯燥
但希望能夠喚起大眾對這兩個定理的重視,以及認識
才疏學淺,還請大家多包涵XD
馬上來吧!
在我國,高中二年級在空間概念的單元中,會學到三垂線定理
我們來看一下,這需要一點的空間想像力
在空間中,若直線PA垂直於平面E於A點,直線L在平面上,且不通過A點
由A點向直線L作垂線,垂足為B點,有線段AB垂直直線L
則:直線PB與直線L垂直於B點
如下圖所示
(圖用小畫家畫,畫得醜還請見諒)
用數學一點的式子來描述是這樣:
直線L,點A在平面E上,且點B在直線L上,點P不在平面E上。
這個三垂線定理闡明了空間中直線與直線垂直關係
也正因為有三個地方垂直,才被稱作三垂線定理
三垂線定理往往容易被人們忽略,被老師忽略、被學生忽略、被大眾忽略,跟其他知名的定理與各種大小公式比起來,這個定理是如此邊緣
一方面這個定理的敘述不容易,很難簡單的講解給別人聽,二來不像某些公式可以輕易地寫或唸出來(和差角公式、指數、對數律 等)
然而,我們來仔細看看課本上常見的證明:
先在直線L上取一點異於B點的C點,會發現三角形ABC、PAB、PAC皆為直角三角形
所以根據畢氏定理:
得證三垂線定理
當然證明方法不只一種,也可在直線L上做兩點C,D,使得BC=BD,最終得到PB是CD的中垂線。
可以自己想想。
相似的也有:
(1)也被稱作「逆三垂線定理」
證明的部分大同小異,(2)稍微特別一些,有興趣者自己試試看吧!
會發現,其實在證明三垂線定理的最後一步,用到了「逆畢氏定理」
大名鼎鼎的畢氏定理,大家都知道
只要是直角三角形,必然有著勾與股的平方和為斜邊平方之關係
然而其逆敘述,知名度卻少了很多
符合兩邊平方和為第三邊平方的三角形,必然是直角三角形
雖然很多人可能會覺得,這不是理所當然的嗎?
可是,要知道,由A推得B,不代表B一定可以推得A,這是很多人會犯的邏輯謬誤
知名的有:一次因式檢驗法、費馬小定理的逆敘述不成立
簡單理解的例子:「人被殺一定會死,但人死不一定是因為被殺」
實際上就是「若P則Q」與「若Q則P」邏輯上是不等價的
所以逆敘述是否成立是必須證明的!
再仔細思考,逆畢氏定理真的有這麼理所當然嗎?真的一定是這樣嗎?
這邊來證明一下,三角形符合兩邊平方和為第三邊平方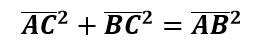
要證明此三角形一定是直角三角形
也就得證逆畢氏定理
符合兩邊平方和為第三邊平方之三角形,必為直角三角形
在國中二年級學生第一次接觸到畢氏定理,然而他的逆敘述,卻少人知
其實在課本也少敘述這個,恐怕是因為在證明的過程中用到了三角形的全等,在學習得當下,第一次接觸畢氏定理是國二上,而全等三角形是國二下才會碰到的,在國二上的那時是不太能證明的。而在後續幾何證明的單元,逆畢氏定理才有機會出現,可能當成一個進階的考題這樣,然而也僅僅是出現,不會強調。
看看108課綱的數學領域課程手冊,其學習內容與學習表現是有提到逆敘述的
(上圖為學習內容,下圖學習表現)
在說明的第六點,特別說明了逆敘述應當放在三角形的全等後在補充
但就這個補充...往往被遺忘,有多少老師真的有補充,又多少學生記得的?
實際上畢氏定理收錄於歐幾里德的《幾何原本》中的第一章 命題47,而逆畢氏定理收錄於第一章 命題48,剛好做為第一章的最後一個命題。
(拍一下我的幾何原本)
我想因為逆畢氏定理的邊緣,或許也連帶影響三垂線定理鮮少人知的一個原因吧,畢竟證明沒有共鳴感。
另一個原因,在高中數學第四冊的編排中,空間概念所學之後便是空間的座標、空間向量的內積、外積,空間中的平面、直線,三垂線定理幾乎沒有上場的機會,(至少很少人會去講它)
在高中的數學課程中,嚴格來說並沒有空間幾何,只有空間概念,純幾何的部分是甚少,多的是用「向量」這一個工具來處理相關問題。想想有了學了空間向量之後,要判斷兩直線是否垂直,基本上都是用兩直線的方向向量之內積去算。
然而三垂線定理還是很重要的,像是這個常見的性質:
正四面體O-ABC的頂點O作底ABC的垂直線,垂足為E,則E為三角形ABC的重心
先畫一個正四面體看看:(令D為BC的中點)
相同的性質也有:
四面體O-ABC,其三角形ABC為正三角形,且OA=OB=OC,頂點O作底ABC的垂直線,垂足為E,則E為三角形ABC的重心
證明差不多,就留給讀者自己證吧
再來就是「兩面角」,空間中兩平面的夾角,也是三垂線定理的應用
先看看兩面角的定義:
空間中兩平面E,F交於一線L,在L上取一點O,E上一點A、F上一點B,有OA垂直L、OB垂直L
則角BOA為兩面角之交角 (也就是下圖中的θ)
如何應用?
由兩面角的定義,先在F上取一點B,對於平面E,作B的垂線,令垂足為A
再作A點對於L的垂線,垂足為O,有OA垂直L
連接OB,即可應用:
由三垂線定理,AB垂直E、OA垂直L,則OB垂直L
因此我們可以面對相關問題了
這邊單單是用空間概念、空間幾何來處理,而非後續的用平面方程式、向量的手法來做。要知道這是兩個完全不同的思路。
馬上來看看三垂線定理的應用:
不作出AB,便無法觀測,也無從應用三垂線定理
然而正是這樣的應用,才發現會有如此特殊關係。這樣便將三垂線定理與兩面角串在一起。
在對岸似乎將這個叫做「三正弦定理」
最後來欣賞幾個題目:
110學測數學的選填G
人的感覺是很不可靠的,單單靠直覺難以判斷空間中的直線與直線是否垂直
正因如此,我們才需要「三垂線定理」!藉由數學定理,我們才能夠確定某些關係。而非靠不準確的直覺。
而「逆畢氏定理」,供我們反思逆敘述是否也成立。要真正去證明才能夠知曉。
依靠這樣的定理,我們才能走下一步,更多步...了解更多數學、探索更多真理與定理。
所以不論是「逆畢氏定理」還是「三垂線定理」都是很重要的!
之前比較怠惰,拖了許久才發
不知道內容會不會太讓人卻步了XD
我相信世上每個數學定理都是很重要的,希望能讓更多人也欣賞到。
沒問題的吧?