題目連結:
題目意譯:
你被給定一個 m × n 整數矩陣 mat 以及一個整數 target�����。
從矩陣每一列選擇一整數使得選擇的數字之總和與 target 之絕對差值最小化。
回傳最小化後的絕對差值。
兩數字 a 和 b 之間的絕對差值為 a - b 之絕對值。
限制:
m == mat.length
n == mat[i].length
1 ≦ m �����、 n ≦ 70
1 ≦ mat[i][j] ≦ 70
1 ≦ target ≦ 800
範例測資:
範例 1:
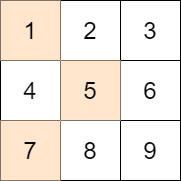
輸入: mat = [[1,2,3],[4,5,6],[7,8,9]], target = 13
輸出: 0
解釋: 一個可能的選擇為:
- 從第一列選 1���。
- 從第二列選 5�����。
- 從第三列選 7��。
選擇的數字之總和為 13,其恰好等於 target�,因此絕對差值為 0�����。
範例 2:
輸入: mat = [[1],[2],[3]], target = 100
輸出: 94
解釋: 最佳選擇為
- 從第一列選 1。
- 從第二列選 2。
- 從第三列選 3。
選擇的數字之總和為 6�����,其恰好等於 target�,因此絕對差值為 94。
範例 3:
輸入: mat = [[1,2,9,8,7]], target = 6
輸出: 1
解釋: 最佳選擇為從第一列選擇 7。
絕對差值為 1。
解題思維:
跟一般的背包問題(Knapsack Problem,如
這題)稍微有點不同:
我們加上第 0 列����,第 0 列可以生出總和 0�����。定義第 0 列到每 i 列每列選一個數字可以得到的總和集合為 S[i],則我們可以看到
S[i] = { x + y | x ∈ S[i - 1] 且 y ∈ mat[i] }
其中 mat[i] 代表矩陣 mat 第 i 列的數字們。注意這邊的 mat 索引值從 1 開始數��。
因此我們可以這樣子一列接著一列生出可能的總和�,跑到最後一列之後掃一次所有可能的總和看哪個最接近 target��,求其絕對差值即是所求����。
此次分享到此為止�����,如有任何更加簡潔的想法或是有說明不清楚之地方��,也煩請各位大大撥冗討論。