題目連結:
題目意譯:
給定一個陣列 nums,其代表著位於 1(含)到 n(含)之間的所有整數之一個排列。我們正要藉由按照給定的順序插入 nums 中的元素到一棵一開始為空的二元樹,來建立一個二元搜尋樹(Binary Search Tree,BST)。請找出有多少不同種的方式可以重新排列 nums,使得由這個重新排列後的陣列建立出來的 BST 與用原先的陣列建立出的 BST 相等。
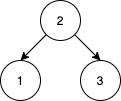
例如說,給定 nums = [2,1,3],我們將會以 2 作為根節點、1 作為左小孩,而 3 作為右小孩。陣列 [2,3,1] 同樣也會得到同一棵 BST,但 [3,2,1] 則不然。
回傳有多少不同種的方式可以重新排列 nums,使得由這個重新排列後的陣列建立出來的 BST 與用原先的陣列建立出的 BST 相等。
由於答案可能很大,將其模 10 ^ 9 + 7 後再回傳。
限制:
1 ≦ nums.length ≦ 1000
1 ≦ nums[i] ≦ nums.length
nums 中所有整數彼此相異。
範例測資:
範例 1:
輸入: nums = [2,1,3]
輸出: 1
解釋: 我們可以將 nums 重新排列成 [2,3,1],而其可以得到與原先相同的 BST。除此之外便不存在其他的排列可以得到相同的 BST。
範例 2:
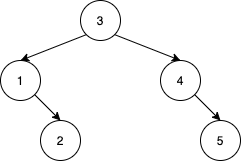
輸入: nums = [3,4,5,1,2]
輸出: 5
解釋: 下列 5 個陣列都會得到相同的 BST:
[3,1,2,4,5]
[3,1,4,2,5]
[3,1,4,5,2]
[3,4,1,2,5]
[3,4,1,5,2]
範例 3:
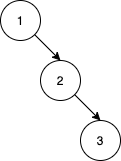
輸入: nums = [1,2,3]
輸出: 0
解釋: 沒有其他 nums 的排列可以得到一樣的 BST。
解題思維:
先只考慮一個節點 i:
如果在 BST 中從根節點(含)到 i(含)的路徑為 x1 → x2 → x3 → …… → xk,則代表著為了到 xk(即節點 i),在 nums 中 x1 要先於 x2 出現、x2 先於 x3、…… 最後才輪到 xk。
因此我們可以把 x1 、 x2 、 x3 等看作是「先決條件」的話,則可以看到我們可以把原始的 BST 看作是
這題的「課程關係圖」。因此 nums 為該 BST 的其中一種拓樸排序,進而可以把本題所求轉換成「有多少種拓樸排序與 nums 等價」。
首先為了找出每個節點之間的條件關係,要先從 nums 建立一棵原始的 BST,參見
這題。
假設現在有一個二元樹是以節點 i 作為根節點。其左子樹有 x 個節點、右子樹有 y 個節點。則這棵樹會得到的可能排列為
(x + y)! ÷ x! ÷ y!
並且乘上左子樹和右子樹各自可能的排列。而要除以 x! 和 y! 是因為對於節點 i 來說,左子樹和右子樹各自的節點內部不能隨便亂排(為了保持 BST 的結構),應視為一體。
可以看到這產生了一個遞迴式出來。而遞迴停止條件則將出現於葉節點,因為沒有可以繼續遞迴的餘地了。
因此我們可以反過來從葉節點把遞迴所需資訊往上推,而我們剛好可以使用上面提及「課程關係圖」來找拓樸排序時用的手法來解——即先找出那些 out-degree 為 0 的節點們便是葉節點(這次因為邊的順序關係,要看的是 out-degree 而不是 in-degree),把這些節點「拔掉」之後會產生「下一批」的「葉節點」。如此便可以依序地把資訊往根節點送。
注意計算過程中應隨時模 10 ^ 9 + 7,以免溢位。而「÷」在模除運算是以「模反元素」(Modular Inverse)的形式出現,求法參見
這題。
最後根節點將得到最終的遞迴結果。但這仍不是答案,因為整個計算過程中會把 nums 這個排列本身也包含答案之中。而所求要的是 nums 以外的排列,因此最後要予以扣除。
此次分享到此為止,如有任何更加簡潔的想法或是有說明不清楚之地方,也煩請各位大大撥冗討論。