題目連結:
題目意譯:
現在有 n 顆燈泡一開始都是關的。接著你先將所有燈泡打開,然後你每二個就把第二個燈泡關掉。
在第三輪時,你每三個燈泡就將第三個燈泡切換狀態(即如果該燈泡是關的,就將其打開;如果是開的,就將其關掉)。對於第 i 輪,你每 i 個燈泡就將第 i 個燈泡切換狀態。對於第 n 輪,你將只會切換最後一顆燈泡。
回傳 n 輪之後,有多少燈泡是打開的。
限制:
0 ≦ n ≦ 10 ^ 9
範例測資:
範例 1:
輸入: n = 3
輸出: 1
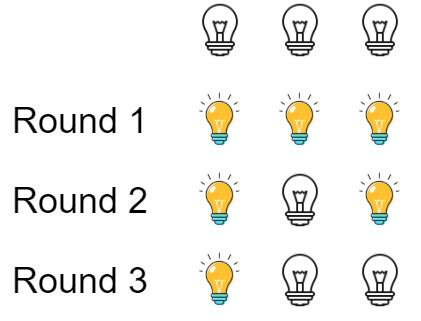
解釋: 一開始,三顆燈泡狀態為 [關, 關, 關]。
第一輪之後,三顆燈泡狀態為 [開, 開, 開]。
第二輪之後,三顆燈泡狀態為 [開, 關, 開]。
第三輪之後,三顆燈泡狀態為 [開, 關, 關]。
所以你應當回傳 1 因為只有一顆是開的。
範例 2:
輸入: n = 0
輸出: 0
範例 3:
輸入: n = 1
輸出: 1
解題思維:
對於第 i 顆燈泡來說,它如果在第 j 輪的時候有被切換,代表著 i 可以被 j 整除。也就是說 j 是 i 的一個因數。
可以看到如果數字 i 有著偶數個因數,則代表著它最後的狀態將會是關的;反之,如果 i 有奇數個因數,則代表著它最後的狀態將會是開的,同時也代表著 i 是一個平方數。
也就是說我們要找出 1(含)~ n(含)之間有多少個平方數,此即為所求。
而這很單純,其恰好為 (√n) 取整數部分個。
此次分享到此為止,如有任何更加簡潔的想法或是有說明不清楚之地方,也煩請各位大大撥冗討論。