題目連結(jié):
題目意譯:
給定一個二元樹的根節(jié)點 root,樹中每一個節(jié)點值彼此相異。
把存在於 to_delete 中的每一個數(shù)值所對應(yīng)的節(jié)點刪除之後,我們會得到一個森林(一群無交集之樹們)
回傳該森林中每一棵樹的根節(jié)點。你可以按任意順序排列。
限制:
樹中之節(jié)點數(shù)最多 1000。
每一個節(jié)點值彼此相異,且數(shù)值位於 1 到 1000 之間。
to_delete.length ≦ 1000
to_delete 包含著彼此相異之?dāng)?shù)值且數(shù)值位於 1 到 1000 之間。
範(fàn)例測資:
範(fàn)例 1:
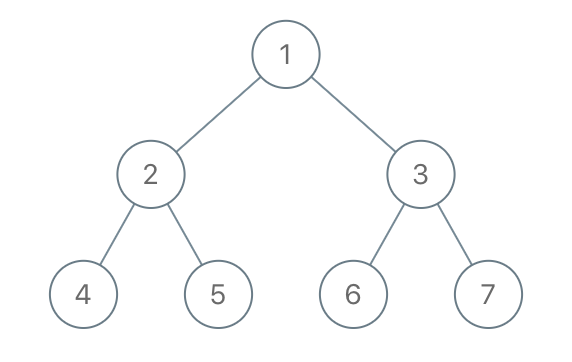
輸入: root = [1,2,3,4,5,6,7], to_delete = [3,5]
輸出: [[1,2,null,4],[6],[7]]
範(fàn)例 2:
輸入: root = [1,2,4,null,3], to_delete = [3]
輸出: [[1,2,4]]
解題思維:
對原本的樹進(jìn)行一次深度優(yōu)先搜尋(Depth First Search,DFS)便可以找到所有要刪除的節(jié)點。
而當(dāng)一個節(jié)點的左小孩或是右小孩被刪除時,連結(jié)到被刪除的子節(jié)點之邊也會被同時刪除。因此這種事情發(fā)生時,要記得把該節(jié)點指向左小孩或右小孩的指標(biāo)清空。
而看完左右小孩的情況之後,如果此時自己本身也需要被刪除,則需要把尚存活著(即本來就存在,且也沒有被刪除者)的左小孩和右小孩作為新的樹之根節(jié)點加到答案中。
而上面這個判斷過程可以直接塞進(jìn) DFS 的過程中,因此掃過一次便可以知道哪些節(jié)點最後會作為根節(jié)點存活下來。而其為所求。
此次分享到此為止,如有任何更加簡潔的想法或是有說明不清楚之地方,也煩請各位大大撥冗討論。