題目連結:
題目意譯:
你被給定一個有著 2 × n 個整數的整數陣列 nums。你需要將 nums 分切成兩個長度為 n 的陣列來最小化兩陣列各自的總和之差值。將 nums 分切,意味著將 nums 中每一個元素放入其中一個陣列中。
回傳最小可能的絕對差值。
限制:
1 ≦ n ≦ 15
nums.length == 2 × n
-10 ^ 7 ≦ nums[i] ≦ 10 ^ 7
範例測資:
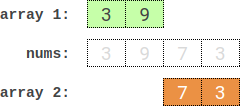
範例 1:
輸入: nums = [3,9,7,3]
輸出: 2
解釋: 一個最佳分切法為:[3,9] 和 [7,3]。
兩陣列各自的總和之絕對差值為 abs((3 + 9) - (7 + 3)) = 2。
範例 2:
輸入: nums = [-36,36]
輸出: 72
解釋: 解釋: 一個最佳分切法為:[-36] 和 [36]。
兩陣列各自的總和之絕對差值為 abs((-36) - (36)) = 72。
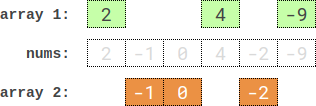
範例 3:
輸入: nums = [2,-1,0,4,-2,-9]
輸出: 0
解釋: 解釋: 一個最佳分切法為:[2,4,-9] 和 [-1,0,-2]。
兩陣列各自的總和之絕對差值為 abs((2 + 4 + -9) - (-1 + 0 + -2)) = 0。
解題思維:
很明顯地,窮舉出所有 2 ^ (2n) 個子集合算出總和不是什麼好辦法。因為根據題目條件最多會出現 2 ^ 30 個子集合,光窮舉出來就會很花時間。
而 nums[i] 的數值範圍也不允許我們來窮舉可能的總和來湊(如
這題)。
還有什麼辦法?可以看到分切後,一組只會恰好有 n 個數字。
因此我們可以先不管三七二十一,把 nums 分成前 n 個數字作為「左半」、後 n 個數字分成「右半」。
而這兩半各自去窮舉出所有可能的子集合之總和,並以挑的數字來分類,即左半挑 1 個數字會有哪些總和值、挑 2 個數字會有哪些總和值等等(右半也同理)。
可以看到總體而言,我們可以從左半挑出 i 個數字(0 ≦ i ≦ n)然後再從右半挑出 n - i 個數字來形成一組。而沒有挑到的數字即是另一組。
但是我們依舊要想辦法處理合併左半挑出 i 個數字、右半挑出 n - i 個數字的各種總和組合。不然如果直接一個一個總和配對,最糟還是會逼近 O((n!) ^ 2) 種組合。
如果現在我們把左半挑出 i 個數字的各個總和值由小到大排序後為 a0 、 a1 、 …… 、 ax,同理把右半挑 n - i 個數字的總和排序後為 b0 、 b1 、 …… 、 by。
再假設 nums 中所有數字的總和為 T。則可以看到 a0 會有三種情況:
1. a0 不管與右半中哪個總和值配對都會大於等於 T / 2;
2. a0 不管與右半中哪個總和值配對都會小於等於 T / 2;
3. a0 + b0 小於等於 T / 2 且 a0 + by 大於等於 T / 2。
先不論情況 1 和 2,情況 3 代表著存在著一個盡可能小的索引值 j 滿足 a0 + bj 大於等於 T / 2。為了方便討論,a1 、 a2 等也都假設是情況 3。
而此時我們可以看到 a1 的 j 值最多只會跟 a0 的「一樣大」;同樣地,a2 的 j 值最多只會跟 a1 的「一樣大」。以此類推。也就是說,當我們從 a0 往 ax 方向走時,每個數字的 j 值只會遞減,絕對不會增加(因為我們已經排序過總和值了)。
那情況 1 和 2 呢?可以看到對於情況 1,我們只要定 i = 0 即可;而情況二則是定 i = y。
所以知道,例如說 a0 + bi 之值,那又如何?
可以看到對於 a0 而言,要湊出「最接近」的 T / 2 的數字只會有 a0 + bi 和 a0 + bi-1 這兩種而已(而且後者可能還不存在;要存在的前提是 i > 0)。因此對於 a0 而言,分切後的總和差值最小值為 min(T - 2 × (a0 + bi), T - 2 × (a0 + bi-1))。
而掃過所有 a 值之後,便可以知道對於當前的左半而言分切後的總和差值最小值為何。然後再掃過所有可能的左半配右半後便可以知道所求。
而我們可以看到這邊時間複雜度最多只會是 O(x) + O(y) + 排序的時間而已。因此總體而言,時間複雜度為 O(2 ^ n) + O(2 ^ n × log(2 ^ n)) = O(n × 2 ^ n)。
因此最後根據上面的方式,我們可以把原本的純窮舉方式 O(2 ^ (2n))「縮減」現在的到 O(n × 2 ^ n)。
從大 O 符號表示法來說變差了,但是如果是套實際上的數值來說。15 × 2 ^ 15 = 491520 是遠小於 2 ^ 30 = 1073741824 的。
以上這種拆分並各自窮舉的方式有一個特殊名字—— Meet In The Middle。此方式在密碼學也會出現,參見
維基。
此次分享到此為止,如有任何更加簡潔的想法或是有說明不清楚之地方,也煩請各位大大撥冗討論。