題目連結:
題目意譯:
你被給定一個大小為 rows × cols 的矩陣 grid,其代表著一個櫻桃園,其中 grid[i][j] 代表著在格子 (i, j) 的位置你可以採集的櫻桃數量。
你現在有兩臺機器人可以幫你採集櫻桃:
位於左上角 (0, 0) 的一號機器人,以及
位於右上角 (0, cols - 1) 的二號機器人。
回傳根據以下規則使用兩臺機器人最多可以採集到的櫻桃數目:
機器人從格子 (i, j) 可以移動到格子 (i + 1, j - 1) 、 (i + 1, j) 或是 (i + 1, j + 1);
當任一機器人經過某個格子時,它會採集所有的櫻桃,使該格變空;
當兩臺機器人同時走到同一個格子時,只會有一者採集櫻桃;
兩臺機器人不論何時都不得走出邊界;
兩臺機器人都應走到 grid 的最後一列。
限制:
rows == grid.length
cols == grid[i].length
2 ≦ rows, cols ≦ 70
0 ≦ grid[i][j] ≦ 100
範例測資:
範例 1:
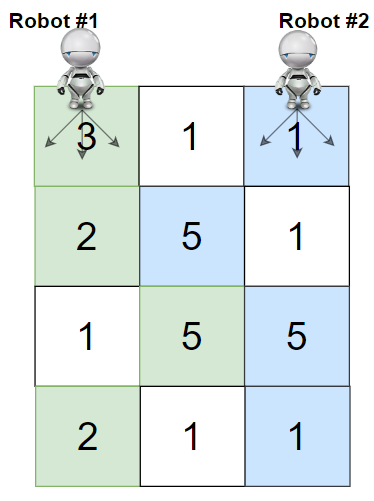
輸入: grid = [[3,1,1],[2,5,1],[1,5,5],[2,1,1]]
輸出: 24
解釋: 在上圖中,一號和二號機器人的路徑分別以綠色和藍色表示。
一號機器人採集到的櫻桃數為 (3 + 2 + 5 + 2) = 12。
二號機器人採集到的櫻桃數為 (1 + 5 + 5 + 1) = 12。
總計櫻桃數為 12 + 12 = 24。
範例 2:
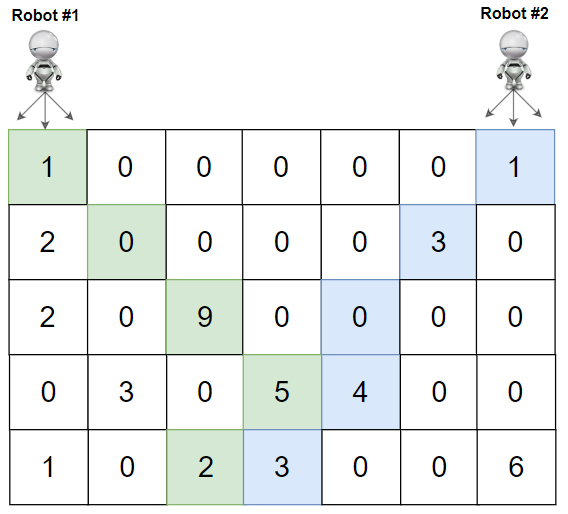
輸入: grid = [[1,0,0,0,0,0,1],[2,0,0,0,0,3,0],[2,0,9,0,0,0,0],[0,3,0,5,4,0,0],[1,0,2,3,0,0,6]]
輸出: 28
解釋: 在上圖中,一號和二號機器人的路徑分別以綠色和藍色表示。
一號機器人採集到的櫻桃數為 (1 + 9 + 5 + 2) = 17。
二號機器人採集到的櫻桃數為 (1 + 3 + 4 + 3) = 11。
總計櫻桃數為 17 + 11 = 28。
解題思維:
跟
這題類似。不過因為現在有兩臺機器人(該題可以視為是只有一臺機器人,且初始位置為第一列的任意位置),所以條件理所當然地會有所變化。
定義一個三維陣列 D,其中 D[i][j][k] 代表著兩臺機器人走到第 i 列且某一臺機器人位於第 j 行、另一臺機器人位於第 k 行的情況下可以採集到的最大櫻桃數。可以看到遞迴式為:
D[0][0][cols - 1] = grid[0][0] + grid[0][cols - 1];
D[0][j][k] = 0,其中 j 和 k 不會同時滿足 j == 0 且 k == cols - 1;
D[i][j][k] = 0,其中 j < 0 或 j ≧ cols 或 k < 0 或 k ≧ cols,而 i 為任意值;
(上面三式為遞迴停止條件)
D[i][j][k] = max(D[i - 1][j - 1][k - 1], D[i - 1][j - 1][k], D[i - 1][j - 1][k + 1],
D[i - 1][j][k - 1], D[i - 1][j][k], D[i - 1][j][k + 1],
D[i - 1][j + 1][k - 1], D[i - 1][j + 1][k], D[i - 1][j + 1][k + 1])
+ G(i, j, k),
其中 i > 0 且 G(i, j, k) 為:
如果 j == k,則 G(i, j, k) = grid[i][j];
反之,則 G(i, j, k) = grid[i][j] + grid[i][k]。
而所求為 max(D[row - 1][j][k]),其中 0 ≦ j, k < cols。
不過,我們如果讓機器人「反著走」也是可以的。只是把兩臺機器人在最後一列的任意位置出發而已(因此更像上面連結的那一題了),最後讓一臺走到 (0, 0)、另一臺則走到 (0, cols - 1)。而陣列 D 的定義和遞迴式只需要稍微修改即可,因此不贅述。
此次分享到此為止,如有任何更加簡潔的想法或是有說明不清楚之地方,也煩請各位大大撥冗討論。