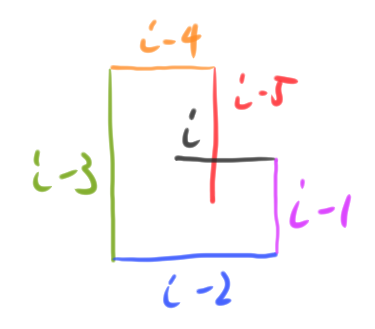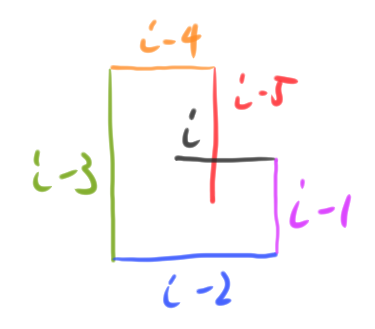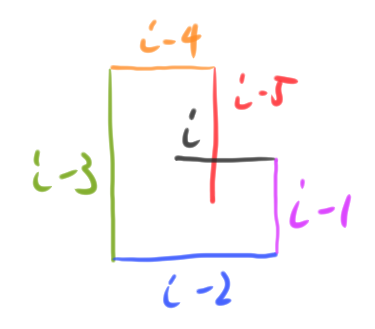題目連結(jié):
題目意譯:
你被給定一整數(shù)陣列 distance。
你開(kāi)始於一個(gè) XY 座標(biāo)平面上的點(diǎn) (0, 0),而你將會(huì)往北移動(dòng)(譯者注:即往 +y 方向)distance[0] 公尺,然後往西(譯者注:即往 -x 方向。此時(shí)剩餘兩方位可以直接對(duì)應(yīng))distance[1] 公尺、往南 distance[2] 公尺、往東 distance[3] 公尺,以此類推。換句話說(shuō),在每一次移動(dòng)之後,你的方向?qū)?huì)往逆時(shí)針?lè)较騺?lái)變化。
如果你的路徑將會(huì)與自身交錯(cuò),則回傳真(True);反之,則回傳假(False)。
限制:
1 ≦ distance.length ≦ 10 ^ 5
1 ≦ distance[i] ≦ 10 ^ 5
範(fàn)例測(cè)資:
範(fàn)例 1:
輸入: distance = [2,1,1,2]
輸出: true
解釋: 該路徑將會(huì)與自身交錯(cuò)於點(diǎn) (0, 1)。
範(fàn)例 2:
輸入: distance = [1,2,3,4]
輸出: false
解釋: 該路徑並沒(méi)有在任何點(diǎn)上與自身交錯(cuò)。
範(fàn)例 3:
輸入: distance = [1,1,1,2,1]
輸出: true
解釋: 該路徑將會(huì)與自身交錯(cuò)於點(diǎn) (0, 0)。
解題思維:
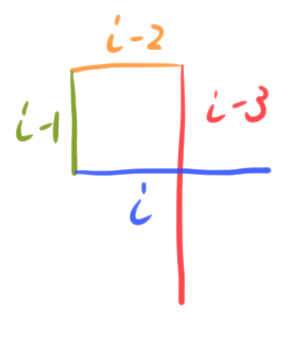
對(duì)於某一條路徑線段來(lái)說(shuō)會(huì)有三種可能的交錯(cuò)方向。
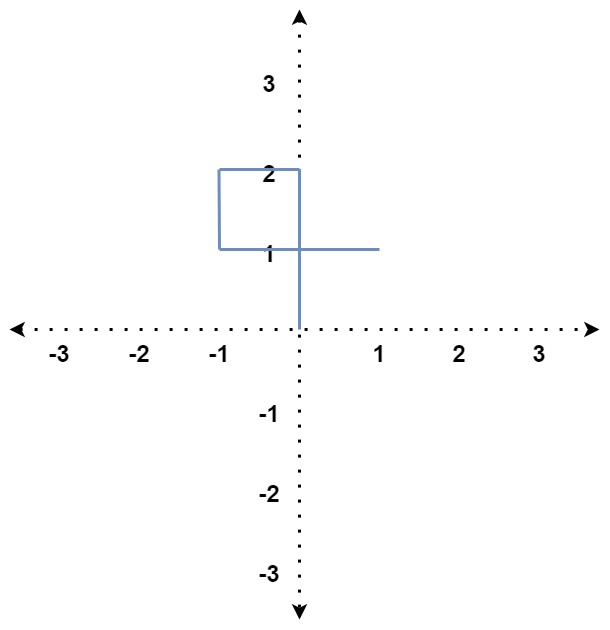
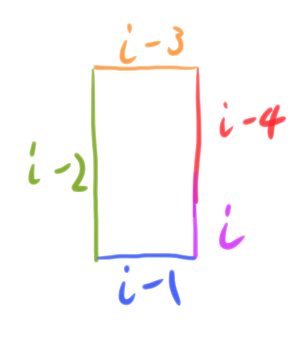
(一)行進(jìn)方向與另一線段的「左側(cè)」交錯(cuò),如下:
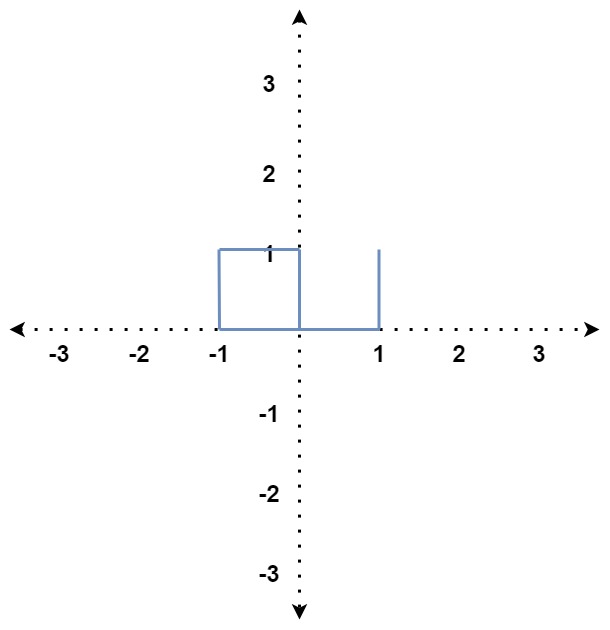
(二)行進(jìn)方向與另一線段的「開(kāi)頭」交錯(cuò),如下:
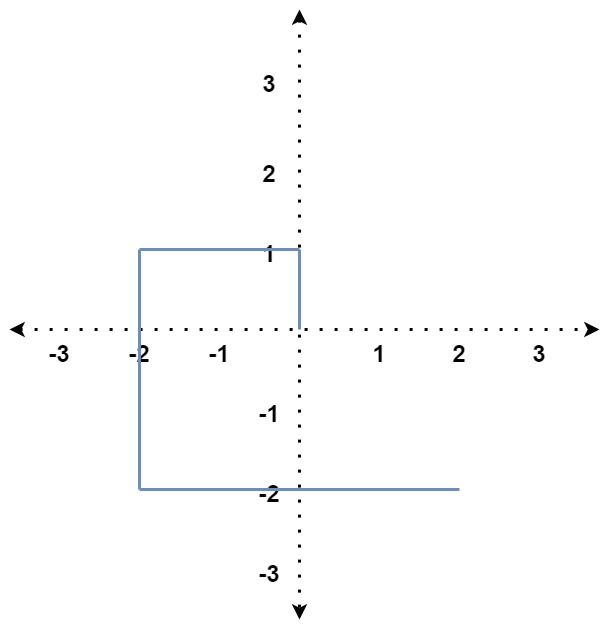
(三)行進(jìn)方向與另一線段的「右側(cè)」交錯(cuò),如下:
至於沒(méi)有第四種的「行進(jìn)方向與另一線段的『結(jié)尾』交錯(cuò)」是因?yàn)檫@樣一來(lái),也必定會(huì)與另一線段的「下一條線段」交錯(cuò)於其「右側(cè)」,因此會(huì)與(三)重複。其他情況(例如說(shuō)繞了好幾圈才回到第一條線等)也是同理,必定會(huì)與其他線段交錯(cuò),因而與(一)~(三)之一的情況重複。
接著,我們一一觀察每一個(gè)情況。
首先是(一):
可以看到要讓線段 i 與線段 i - 3 交錯(cuò),需要滿足
1. distance[i] ≧ distance[i - 2],不然上圖的線段 i 會(huì)不夠長(zhǎng),碰不到線段 i - 3
2. distance[i - 1] ≦ distance[i - 3],不然線段 i 再長(zhǎng),依舊也碰不到
接著是(二):
可以看到要讓線段 i 與線段 i - 4 交錯(cuò),需要滿足
1. distance[i] + distance[i - 4] ≧ distance[i - 2],不然線段 i 碰不到
2. distance[i - 1] == distance[i - 3],不然無(wú)論如何都無(wú)法剛好碰到線段 i - 4 的「開(kāi)頭」
最後是(三):
可以看到要讓線段 i 與線段 i - 5 交錯(cuò),需要滿足
1. distance[i] + distance[i - 4] ≧ distance[i - 2],不然線段 i 碰不到
2. distance[i - 2] ≧ distance[i - 4],不然線段 i 碰到的會(huì)是線段 i - 3,而此時(shí)會(huì)變成(一)的情況
3. distance[i - 1] + distance[i - 5] ≧ distance[i - 3],不然線段 i 依舊碰不到
4. distance[i - 1] ≦ distance[i - 3],不然此時(shí)線段 i 雖然可能依舊會(huì)碰到線段 i - 5 甚至是線段 i - 4,但現(xiàn)在線段 i - 2 必定會(huì)碰到線段 i - 5,因此會(huì)變成(一)的情況。
而我們只要對(duì)於每一個(gè)線段長(zhǎng)度 distance[i] 跑過(guò)以上三種判斷條件便可以知道線段 i 有沒(méi)有「先前」其他線段交錯(cuò),如果有就回傳真;反之如果掃過(guò)整個(gè)陣列 distance 之後都沒(méi)有遇到,則回傳假。
此次分享到此為止,如有任何更加簡(jiǎn)潔的想法或是有說(shuō)明不清楚之地方,也煩請(qǐng)各位大大撥冗討論。