今天要來介紹一個好玩的數學邏輯小遊戲
不分男女老少、貧富貴賤、人人皆可上手
也不用多高深的數學,人盡皆可挑戰!
Renzoku (連續)
遊戲規則
1. 每個列與行 數字不得重複
2. 兩個方格之間黑點代表該兩個方格為「連續」的數字 (例如:1和2)
3. 如沒有黑點則「不得」為連續的數字。
其實就是數獨的變形版本
不過少了九宮格的限制
但增加的"連續"規則讓遊戲方法變化了一些
這邊的連續指的是連續相鄰的數字,並非微積分上的連續XD
我都是在這個網站上遊玩的,也都在這邊截圖
(此網站還有許多數學邏輯小遊戲 數謎、數橋、 等等 有興趣一定要多看看來玩玩)
好比這個最簡單的4X4 (右邊只是遊戲介面 提醒你是填入1-4)
別看它只有一個4 就不知道怎麼辦了
(在數獨中 確實只有一個4,會完全不知道怎麼辦,畢竟有好多解
利用連續的特性,可以知道第二行 依序為 1,2,3,4
還有第四列由於4的左右都不連續,代表一定是1,2,最右邊就是3
依此推理,很快就能解出全部...
最後可以解得
基本上可以從網站上挑戰不同難度的題目
我的話會覺得 7X7 以上就偏難了,無法光用看的就推出8 9 成
通常就要不斷的試誤窮舉與推理
以下來示範7X7 的普通難度 的解題過程,有更好的做法也都歡迎討論
沒錯,就算來到7X7 初始情況還是只有一個7
就是這題原始條件特別嚴苛才挑這題的
為了求溝通的方便,將其視為一個矩陣,每個位子將用a(n,m) 表示 第n列 m行的元素是什麼
1. 根據連續特性,5列的 7旁邊必然是 7,6,5
順便把可能的數字填上去
一定要注意,沒有黑點=不連續 不相鄰的數 必須善用這個性質
左上角的 不要理它...
以為沒辦法? 不可能做下去了?
沒有,就真的去試誤窮舉吧!
2.假設 a(5,1)的數字 做討論
發現皆有矛盾 不可行
而a(5,1)=3 , 必須分兩個情況討論,有a(5.2)=2 或 a(5,2)=4 這兩種情況 都要看看
a(5,2)=4 這情況才是符合的, (注意 如果有兩個都符合 那未必能確認)
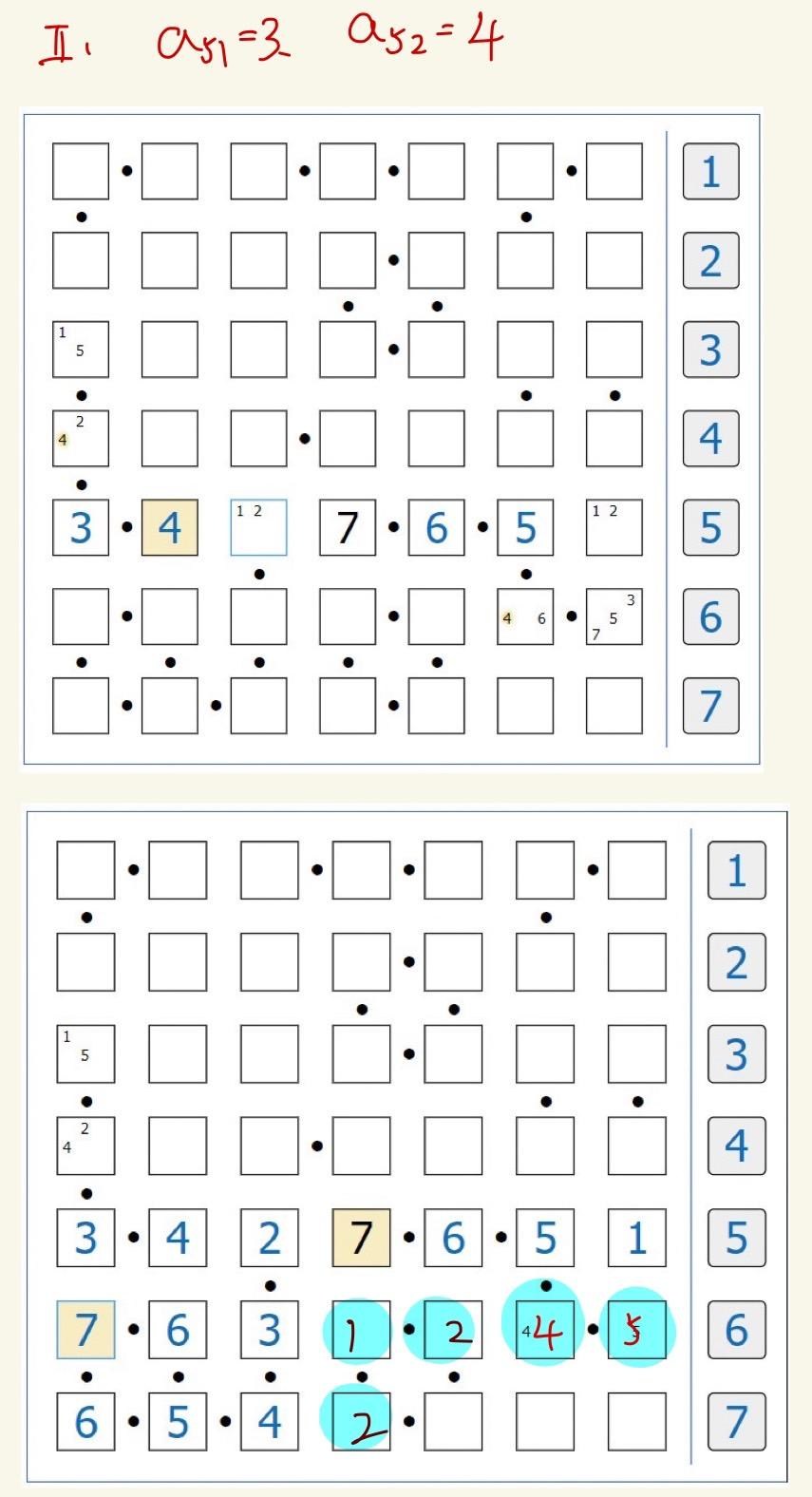
既然符合,那就把剩下的填上
以及第6列,剩下的補齊
3. 注意第6行的情況 用連續的特性做分類討論
第6行剩下 {1,2,3,6,7}
還會有兩組連續,以及一個獨立的數字,那麼 a(7,6)不可能會是6或7
a(7,6)將會是1
此時 將可以填入其他格
以及第1列的綠色三格必然會是(3,4,5) 或 (5,6,7) 這兩種情況
4. 針對第5行討論
第5行剩下 {1,4,5,7}
會有1組連續,連續的那組必然是4,5
可確定a(4,5)=1 , 第一列的三格必然為(5,6,7)
再確定上圖中藍色的a(4,3)=6 ,a(4,4)=6
以及綠色的 a(2,4)=4 ,a(3,4)=3
從而判斷 第5行 的 a(2,5)=5 ,a(3,5)=4
5. 針對第6行做討論
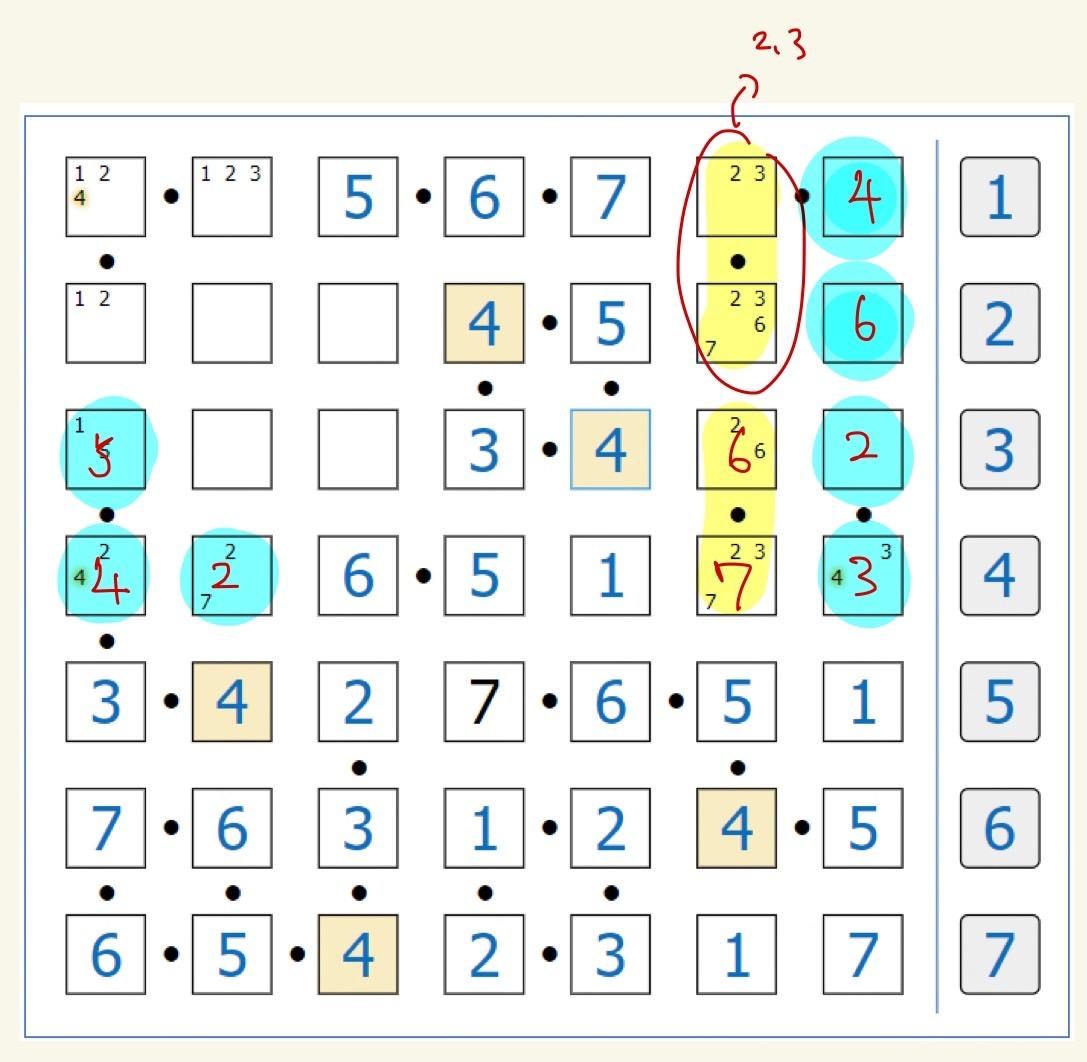
第6行只剩下(2,3) (6,7) 兩組連續
但第一列已經出現6,7,所以必然(2,3)這組在上面
確認後即可將藍色部分依序填出來~
基本上到這邊已經算是尾盤解決了
剩下幾格 一定能夠完成
最後得到:
有沒有很有趣?
明明一開始的條件如此嚴苛(49格中只給了1個數字)
可是卻能夠靠著層層推理,破解完成它!
這就是數學的奧妙與這遊戲的精妙之處了
這個遊戲名子取得很好,「連續的數字」,只是在離散世界的連續,並非實數的連續
好好體會連續的數字吧,數字自有其奧妙
衍伸思考:
1.如何創造出相關的連續謎題?
2.能夠有唯一解最少的條件為何? nxn的情況下,至少需要幾個數字? 能夠一般化解出嗎?
我也不知道,但光是體會這個就足夠有趣
值得好好研究的問題
相關的問題是數獨的情況
可參考:700萬小時搞定最小數獨問題
最少必須給定17個數字才能確定9x9數獨唯一解