上回提到橢圓面積,
發現漏講了橢圓的標準式。
橢圓的標準式長這個樣子:
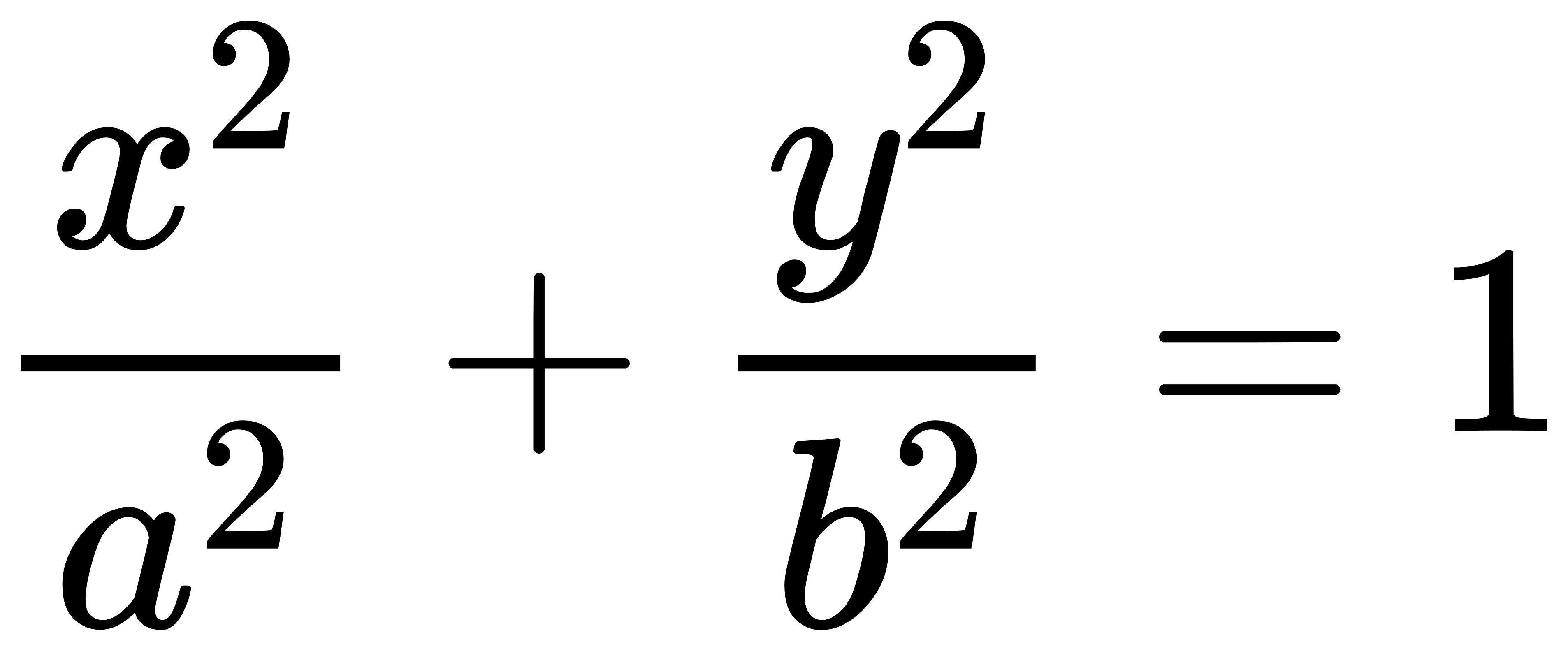
如果 a=b=r,
那這不就是一個正圓嗎?
那這個方程式就會長成這樣:

其實很好理解。
如果原點是圓心,
那麼圓上的每一個點到圓心的距離都等於半徑 r,
這是圓的標準定義。
透過畢氏定理,
特定座標點 (x,y) 到圓點的距離,
就是 x 座標平方加上 y 座標平方後開根號,
而這個長度正好就是半徑 r,
因此很容易可以連想到這個式子。
但是橢圓呢?
其實上回有提到,
橢圓的參數式為:
x = a cos(t)
y = b sin(t)
我們將第一個式子等號兩邊都除以 a,
將第二個式子等號兩邊都除以 b,
接著平方鄉加就會得到這個方程式:
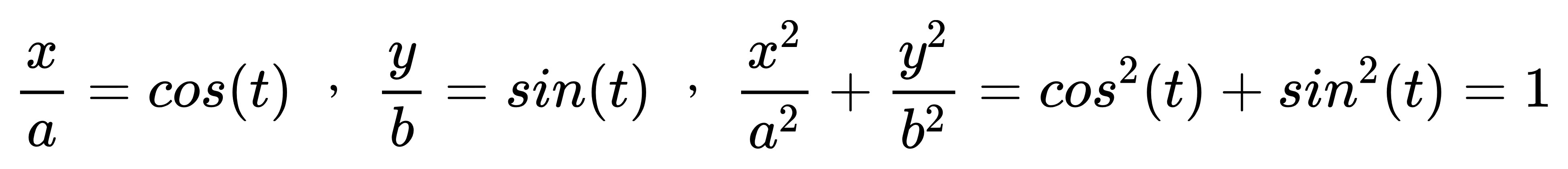
很容易就能找到橢圓的標準式。
如果不透過參數式,
而是透過橢圓的直接定義:「橢圓上任意點到兩焦點的合計距離為常數(等於長軸長度)」也可以證明,
不過這就稍微有點複雜。
橢圓的焦點一定在長軸上而且對稱,
所以我們就令焦點的座標為 (-c,0) 與 (c,0)。
於是利用 (x,y) 到 (-c,0) 與 (c,0) 的長度合計可以得到這個方程式:
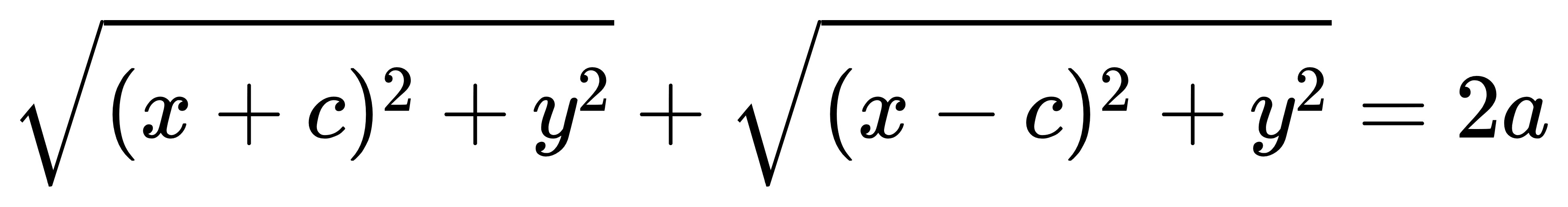
(2a = 長軸長度)
移項:
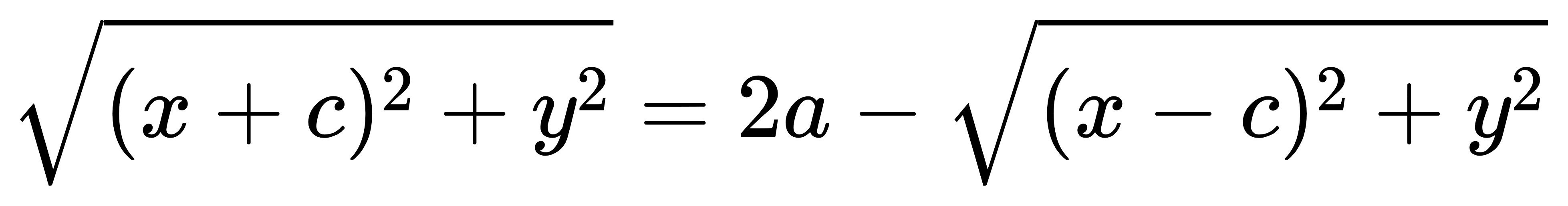
兩邊平方:

拆開括號化簡,
x、y、c 的平方項會消除掉,
接著把兩邊的 cx 項合併,
就能把 4 也約掉。
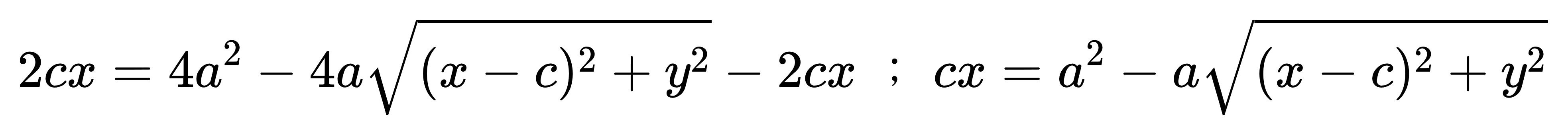
移項再平方:
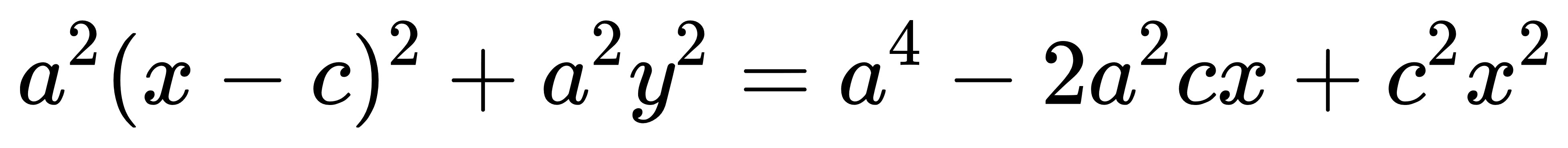
乘開化簡:
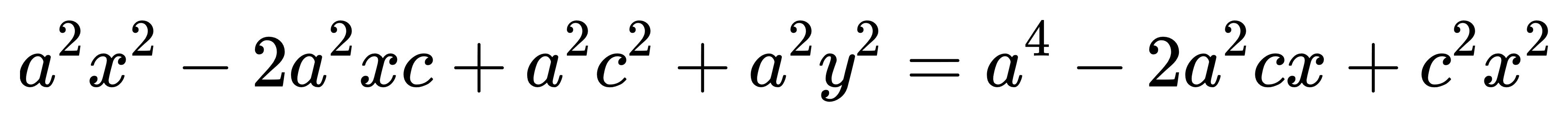
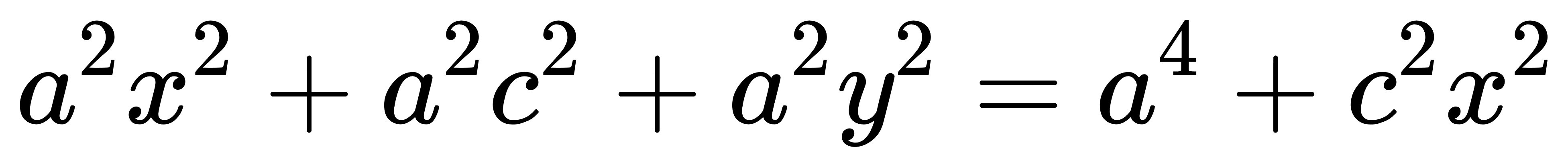
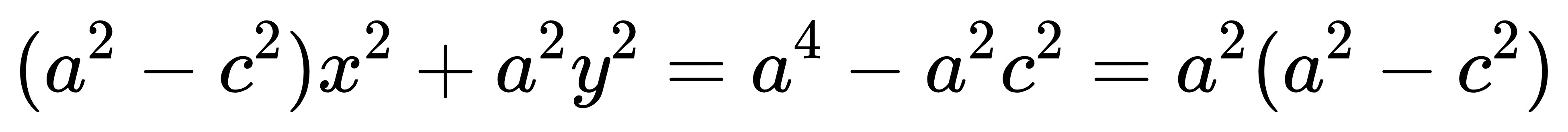
把整個等號右邊除過來:
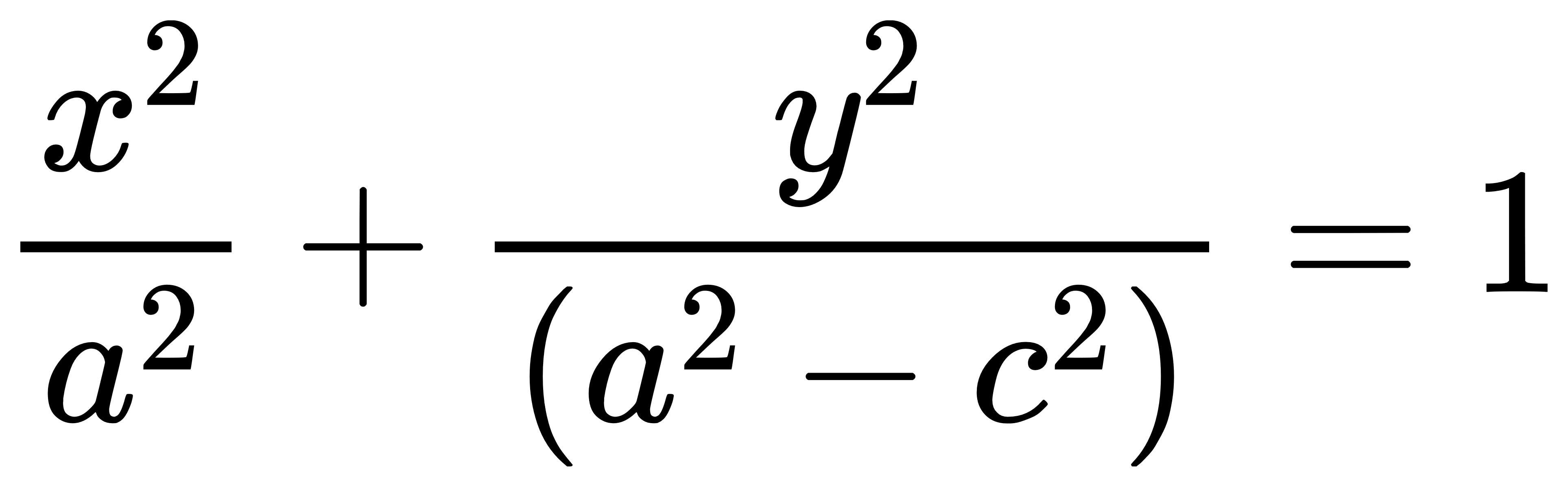
這時已經頗具雛型了對吧。
可是這裡並沒有出現 b 啊!
沒關係,
把 (0,b) 這個點帶入,
就這個點來說,
他與兩焦點的距離正好相等,
所以會得到這個方程式:
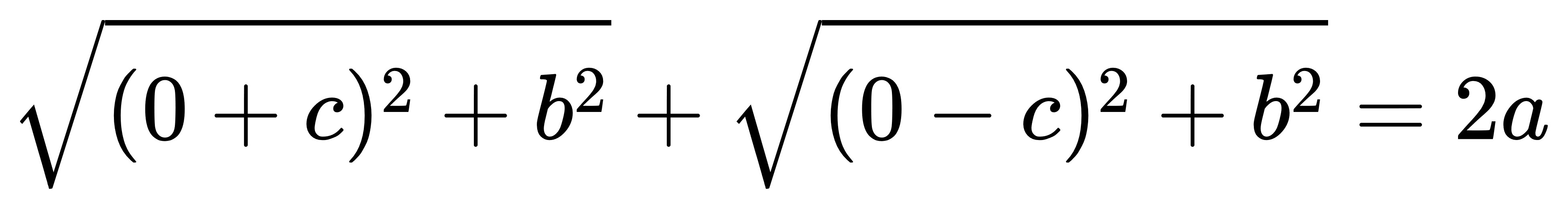
整理一下得到:
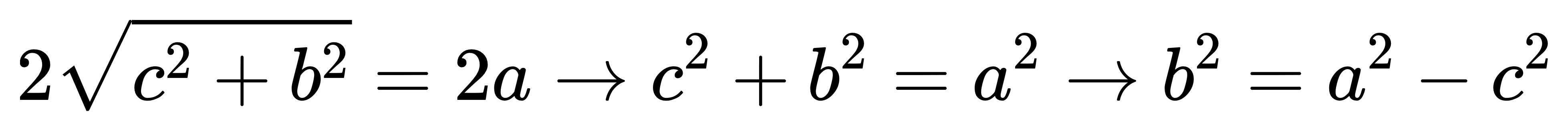
將結論帶進去就得到了標準式:
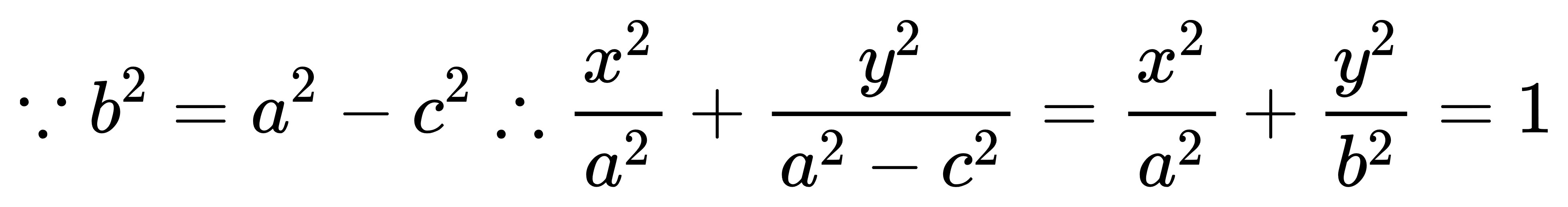
而上回的證明也提到了三角函數的恆等式,
因此這裡就順便說明一下:
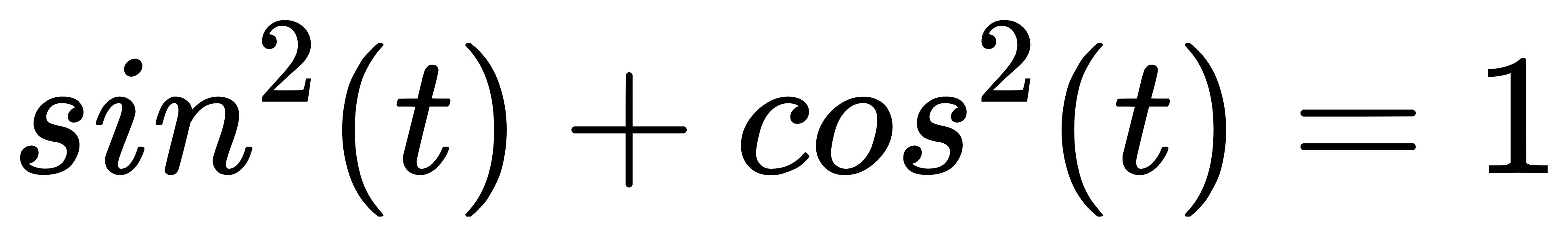
這個簡單到不行了。
一個具有角 t 的直角三角形,
令斜邊為 c、對邊為 a 、鄰邊為 b,
是不是可以得到這個結論:
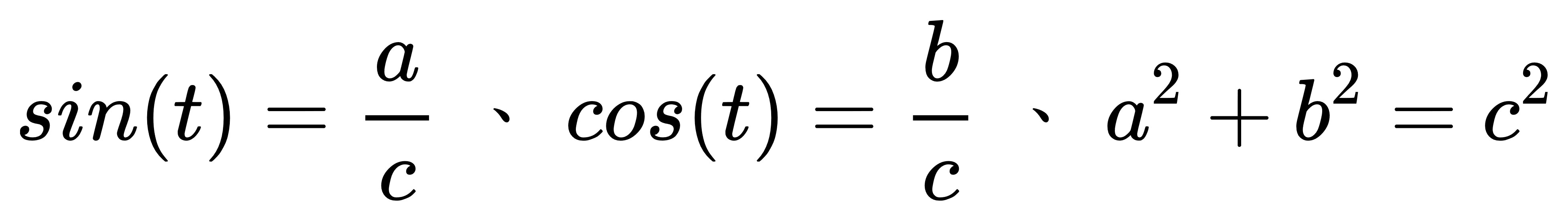
那麼:

這不就出來了嗎?
和角公式:
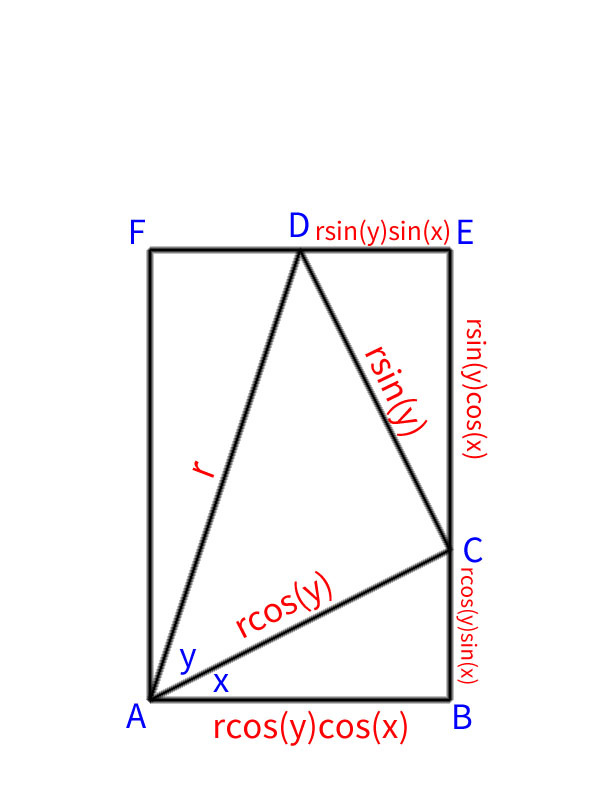
看上面這個幾何圖形,
看三角形 ACD
令 AD=r,
那 CD 就等於 r sin(y);
CA 就等於 r cos(y)。
看三角形 ABC,
CA 為 r cos(y),
那 BC 就等於 r cos(y) sin(x);
BA 就等於 r cos(y) cos(x)。
再看三角形 CDE,
CD 為 r sin(y),
那 ED 就等於 r sin(y) sin(x);
EC 就等於 r sin(y) cos(x)。
角 ECD 正好為 x 應該看圖解都能推算出來才對。
(∵角 ACD 為直角)
有了這些關係長度以後,
sin(x+y) 不就出來了嗎?
它等於 BE 除以 r,
而 BE 又等於 BC+CE,
所以得到:
sin(x+y) = sin(x) cos(y) + cos(x) sin(y)。
口訣:「殺加 等於 殺摳 加 摳殺」。
同樣的。
cos(x+y) 也出來了嘛!
它等於 FD 除以 r。
而 FD 等於 AB-DE,
注意這裡是減號,
所以得到:
cos(x+y) = cos(x) cos(y) - sin(x) sin(y)。
口訣:「摳加 等於 摳摳 減 殺殺」。
然後 tan(x+y) 其實也出來了,
它就是 sin(x+y) 除以 cos(x+y),
只是稍微複雜一點需要運算,
但也還好:
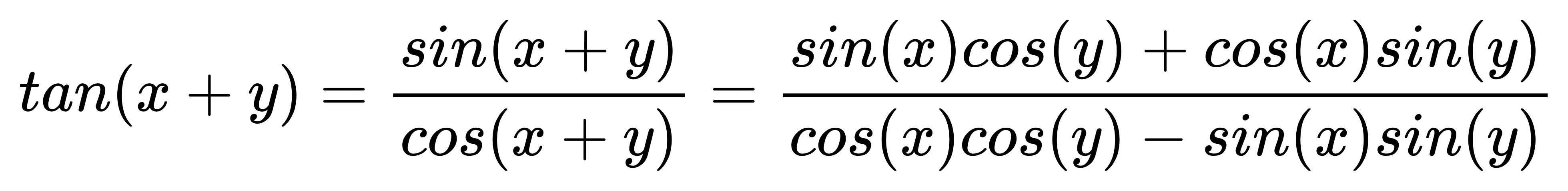
看起來很亂,
把分子分母都分別除以 cos(x)cos(y):
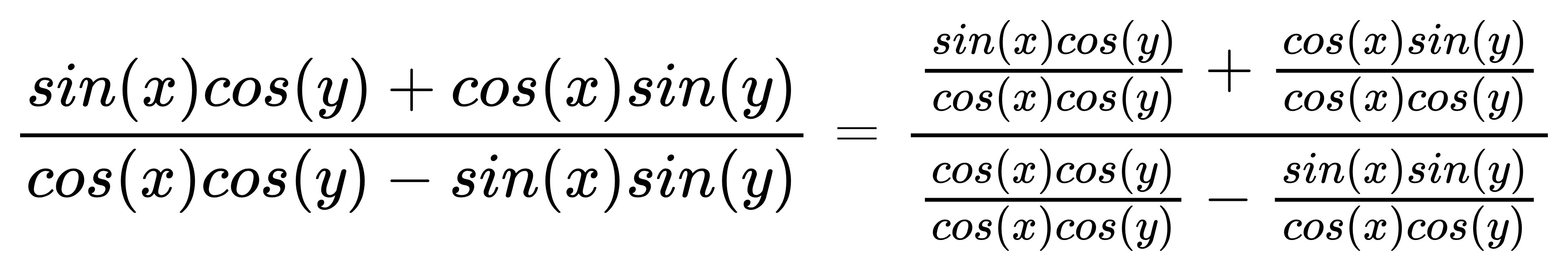
約分化簡:
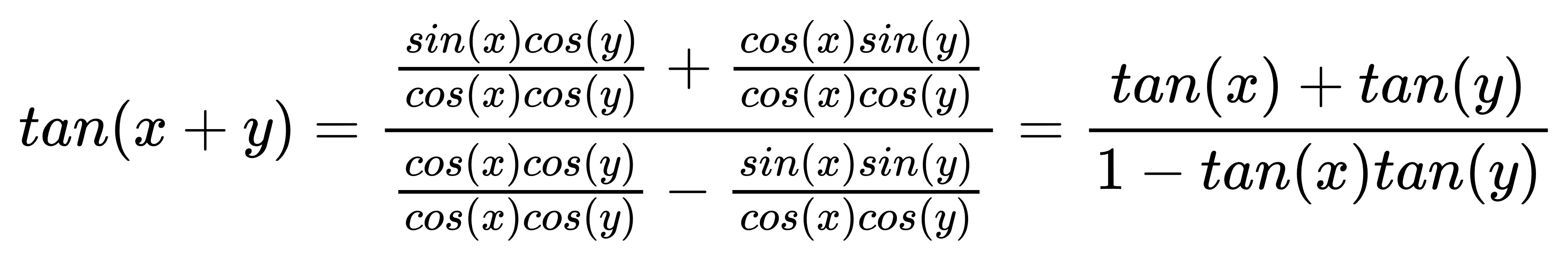
這樣就好了。
差角公式:
差角公式其實就是和角公式的一個特例。
你把 y 變成 -y 不就好了嗎?
因為 sin 是奇函數,
所以 sin(-y)=-sin(y);
而 cos 式偶函數,
所以 cos(-y)=cos(y)。
我們利用這個結論帶進去就好:
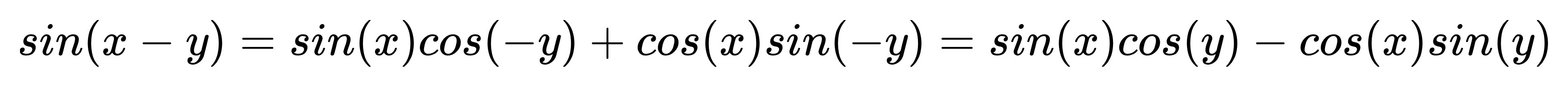
sin 的差角跟和角一樣,
只是加號改減號。
口訣:「殺減 等於 殺摳 減 摳殺」。

cos 的差角公式也一樣,
但是減號改加號。
口訣:「摳減 等於 摳摳 加 殺殺」。
因為奇函數除以偶函數仍是奇函數,
所以 tan 是奇函數,
也就是說 tan(-y)=-tan(y),
所以:
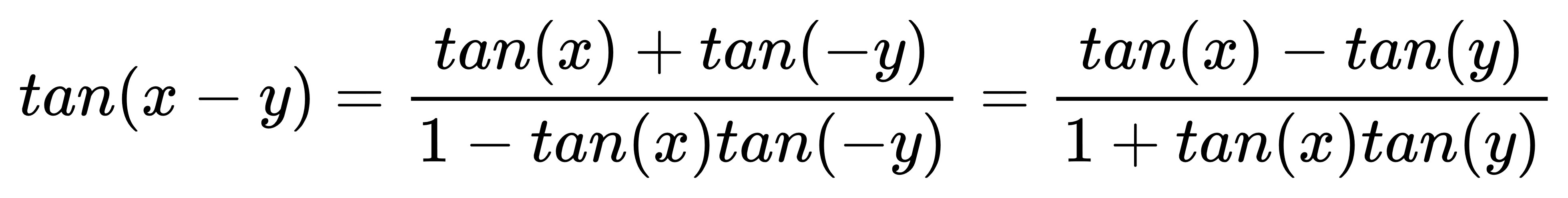
倍角公式:
知道了和角公式,
那倍角公式不就是當 x=y 時的和角公式嗎?
因此:
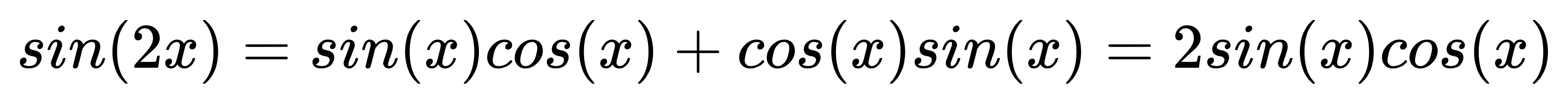
口訣:「殺2=2殺摳」
同樣的:
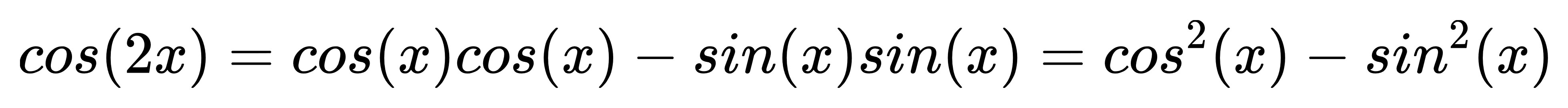
口訣:「摳2=摳平方-殺平方」
不過這個公式雖然漂亮好記,
但卻不好用。
帶入 sin、cos 的平方和等於 1 進去運算,
我們會得到更好用的公式:
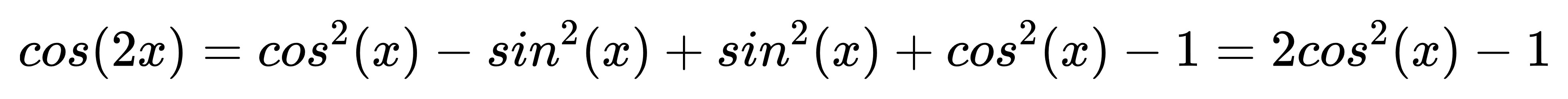
以及:
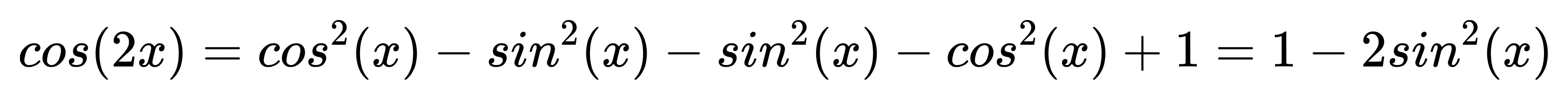
這個為什麼好用呢?
因為積分時會用到。
sin、cos 的平方要積分直接積不好積,
把它化成 cos(2x) 來積分不就很簡單嗎?
也就是說,
上述兩式更好的寫法是:
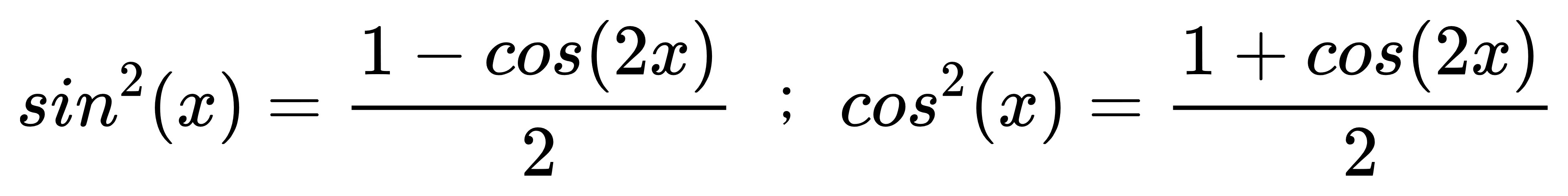
tan 的倍角公式就還好,
不過依樣畫葫蘆:
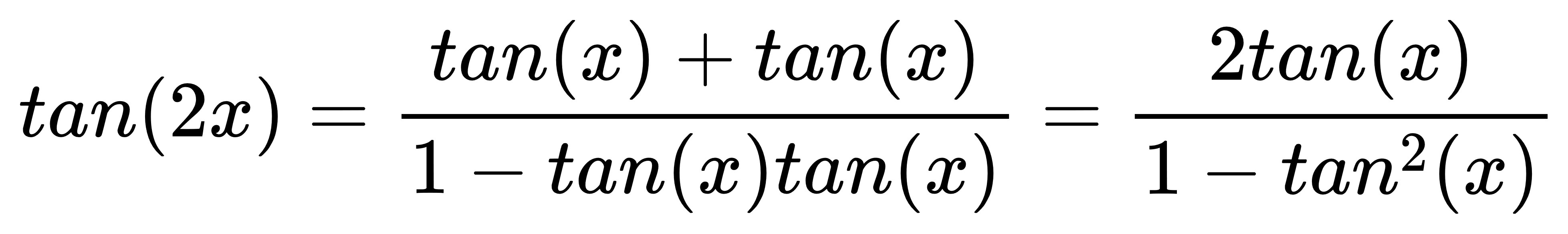
化簡一下:

不過這個就比較沒那麼好用,
通常會把 tan 改成 sin 與 cos 的形式來做會比較多。
半角公式:
半角公式是從倍角公式推導出來的。
前面提到:

那麼在已知 cos(2x) 的情況下,
經過移項,
反過來也能求出半角的 sin(x)、cos(x) 的數值。
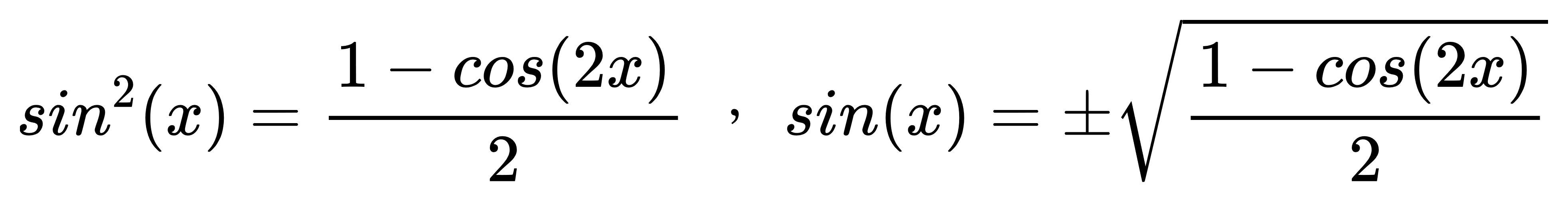
半角公式需要開平方根,
所以該取正還取負具體得根據 x 的大小去做判斷才行。
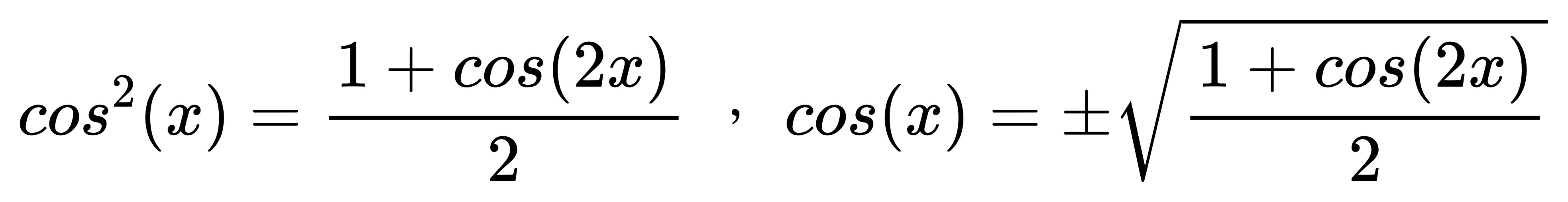
同樣的也需要開平方根,
因此正負號一樣要根據 x 的大小去取值。
三倍角公式:
三倍角公式就比較有點無聊一些,
因為萬變不離其宗。
帶入和角公式:
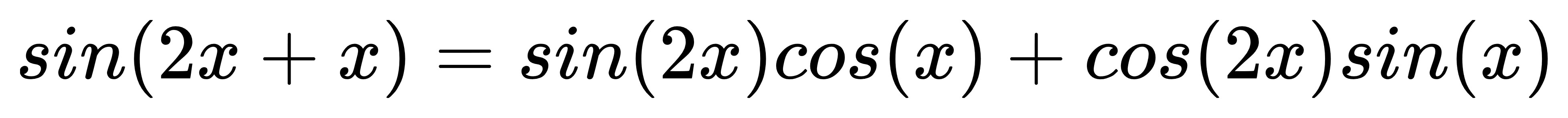
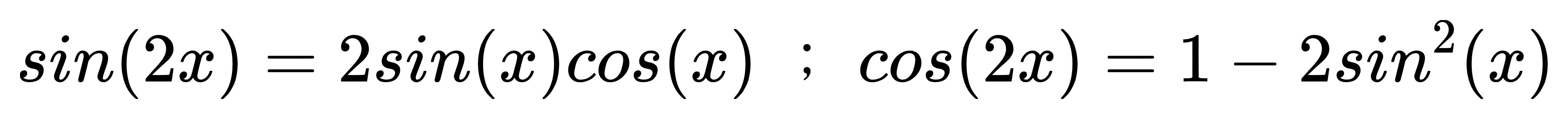
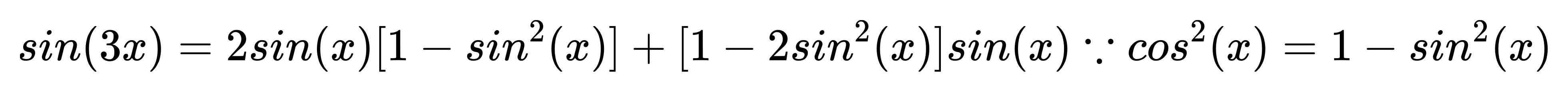

看得出來,
這個公式非常硬湊,
而且不好記。
同樣的:
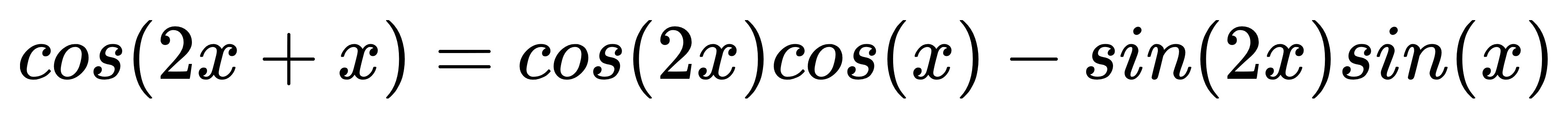
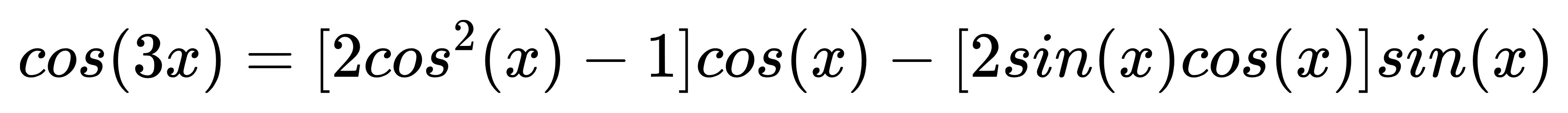

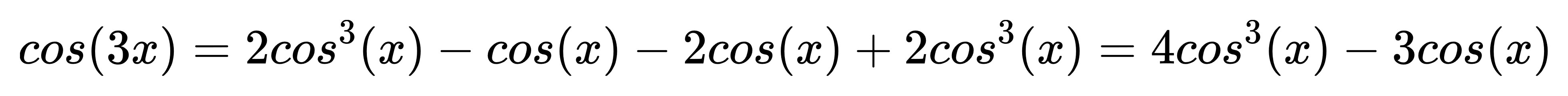
這個稍微好記一點:
口訣:「摳三 等於 四摳三 減 三摳」。
(臺語:一塊三 等於 四塊三 扣掉 三塊)。
【後記】
別看亞夜這幾個禮拜推三角函數推得信手拈來,
其實除了最基本的那幾個以外亞夜通通沒有背,
因為真的難背得要死。
亞夜有一本筆記本將這些結論抄起來,
就像查表一樣方便隨時查閱,
但是考試的時候如果不是翻書考就沒輒,
亞夜考大學時數學 14 級分肯定就是敗在公式沒有背(並沒有

封面圖片:AI生成
本篇使用的方程式編輯素材來自:LaTeX公式編輯器

