這裡亞夜。
今天來說一下,
「橢圓的面積」是怎麼算出來的。
在這之前要說明的是,
就像圓有一個很重要的參數叫做「半徑」一樣,
橢圓也有類似的參數叫做「半長軸」跟「半短軸」,
會如這張圖這樣定義:

如果我們把橢圓的圓心放在原點,
把長軸對齊 X 軸,
那麼短軸就會自動對齊 Y 軸,
這時橢圓就會與 X 軸、Y 軸相交於 4 個點,
而當中 a 就是半長軸的長度,
而 b 就是半短軸的長度。
那我們要怎麼來表示這個橢圓呢?
我們分別以半徑 a 與半徑 b 各做一個輔助圓:
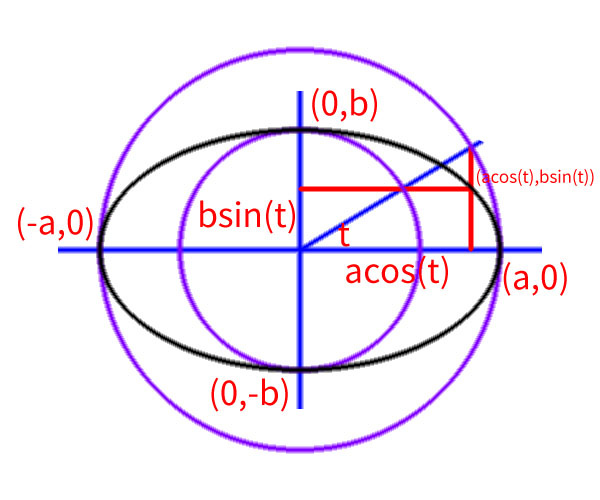
我們從圓點做一條射線,
與 X 軸的夾角為 t。
這條射線分別會與大小圓各相交於一點。
根據圖上的幾何關係,
我們可以利用這條射線去定義橢圓上的一個點,
該點的座標為 (acos(t),bsin(t))。
因此我們得到橢圓的參數式為:
x = a cos(t)
y = b sin(t)
接著我們只需要對第一象限做積分,
就能求出橢圓第一象限的面積。
求面積很簡單嘛,
只要把高度 y 呈上寬度 dx 就能得到一小條的面積對吧?
然後從 0 累加到 a 所有的小條面積就是整個第一象限的面積了嘛,
於是我們等於是要做這個積分:
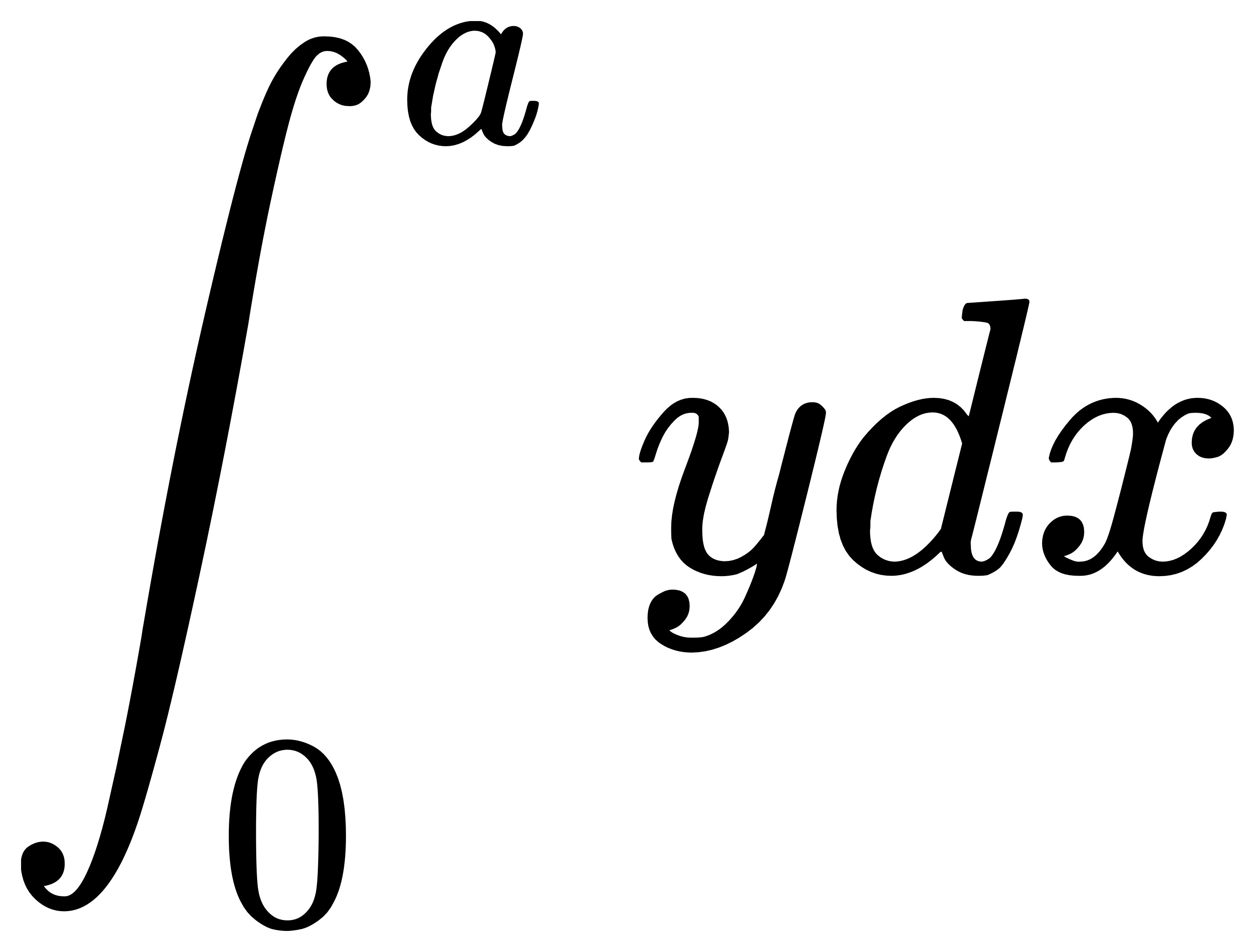
我們這裡做一下變數變換,
x = a cos(t),
那麼 dx = -a sin(t) dt。

關於三角函數取導數請參考這一篇,
這裡就簡單帶過去。
帶入 y 跟 dx,
我們可以將這個積分變換成:

因為 ab 都是常數所以可以提出來,
上下界交換會差一個負號所以負號消掉,
因此可以化簡為後面的樣式。
然後根據三角函數的倍角公式,

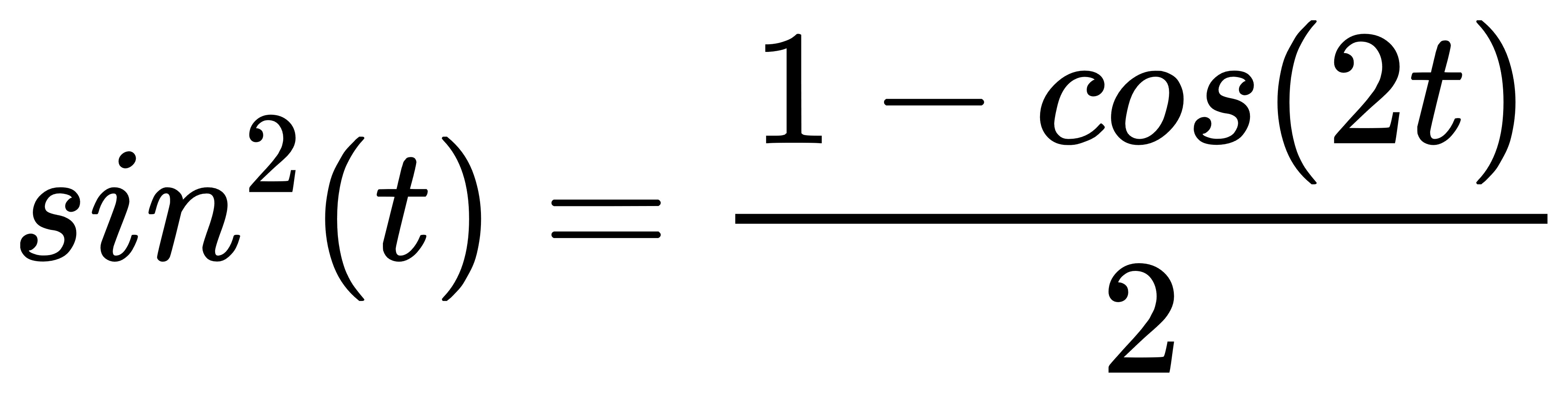
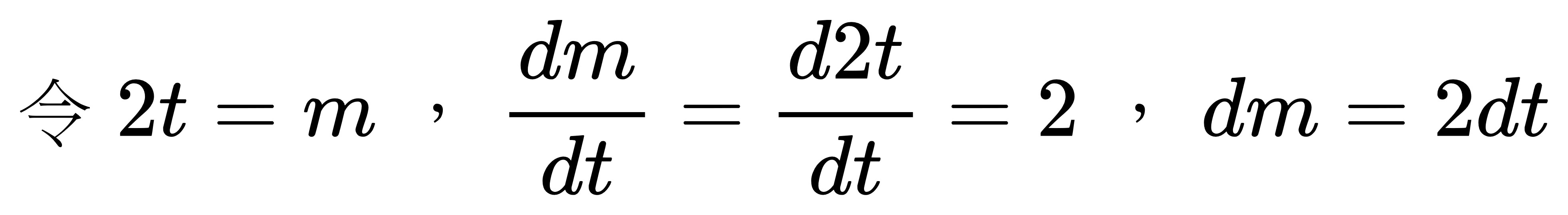
因此原式可以寫成:
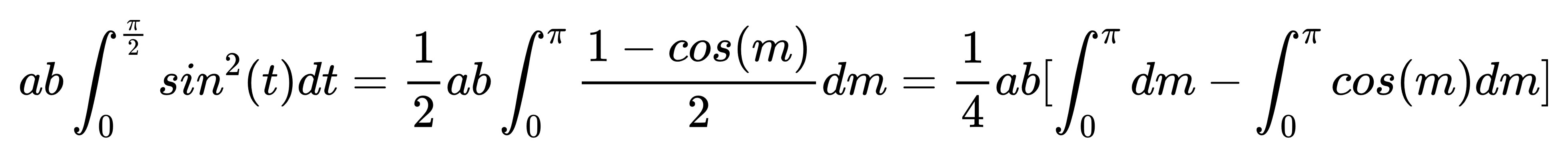
解釋一下,
因為 dm = 2dt,
所以我們要湊出 dm 就必須把原是乘以 2 才有辦法湊出 2dt。
那既然乘以 2 當然就要把他除回去才會相等,
因此提了一個二分之一到積分符號外面。
又因為 m = 2t,
所以 t = 二分之 π 時 m = π,
因此積分上下界變成 0 到 π。
最後當然就是把裡面的二分之一再提出來,
然後分別對 1 跟 cos(m) 積分就好。

dm 積分出來帶入上下界後是 π,
cos(m)dm 積分出來是 sin(m),
帶入上下界不論是 sin(π) 還是 sin(0) 都是 0,
所以後面那一項就是 0 也就不必管他,
因此最後算出來就是四分之一個 πab。
既然第一象限的面積是四分之一個 πab,
那全部四個象限的面積加總不就是剛好一個 πab 了嗎?
因此我們得到橢圓的面積公式為 πab。
題外話,
如果半長軸等於半短軸,
那這個橢圓是不是就剛好是一個正圓呢?
因此圓是橢圓的一個特例,
當然圓的面積也可以帶橢圓面積公式去求解。
如果半長軸等於半短軸,
意味著 a=b=r,
所以圓面積公式是 πr 平方沒問題。

封面圖片:AI生成
本篇使用的方程式編輯素材來自:LaTeX公式編輯器

