最近ho圈是不是在流行數學啊XDDD
其實,
微分這東西的觀念很簡單,
那就是「變化率」。
所謂的函數,
指的就是包含一個或數個變量的公式,
只要帶入變量就能算出不同的結果。
舉例來說,
f(x)=7x+3這個函數,
就是一個帶變量x的函數。
如果給定x=1,
那麼f(1)=10;
如果給定x=2,
那麼f(2)=17。
那什麼叫做變化率呢?
簡單的說就是針對函數上的某一個點,
這個點上的變化的趨勢。
也就是說,
如果給定的變量產生了改變,
那麼函數直又會怎樣的改變,
這就是變化率的意義。
那麼很簡單嘛!
我們就在函數上取兩個點,
分別是變量x=a跟變量x=b,
這樣我們就會得到兩個函數值f(a)跟f(b)。
那麼,
「變化率」不就是「變化量」÷「變數間的差異量」嗎?
舉例來說,
早上9點時我人在高雄,
早上10點時我人就到臺北了,
那麼我位置的變化率就是高雄跟臺北的距離除以花掉的時間,
想必你也已經想到了,
這個概念就是「速率」。
當然,
這樣求出來的「速率」只能是平均速率,
如果今天要表達「某一個瞬間」的速率怎麼辦呢?
那就只能取「那一個瞬間」的位置變化來除以「那一個瞬間」,
得出來的就是那一個瞬間的速率了。
好,
點到即止,
這些是高三數學就會教的基本功。
嘛,
高三才教老實說有點太晚了,
因為你國中物理在算速度位移的時候就會需要有這些觀念了,
但就因為當時的數學還沒有教到「導數」的觀念,
導致學生都只能繞遠路用圖解的方式去算(攤手
好啦切入重點。
高三教導數的時候,
應該很多人都會聽過一個口訣:「指數拿下來當係數,指數減一」。
其實,
這個口訣只針對「多項式函數」的導數適用。
具體為什麼適用,
很多老師都沒教,
就只是像九九乘法表一樣要學生背起來(攤手
至於為什麼以及這個口訣的證明則講都沒講。
其實這個證明簡單的要命就是了。
首先,
接著我們就能得到,
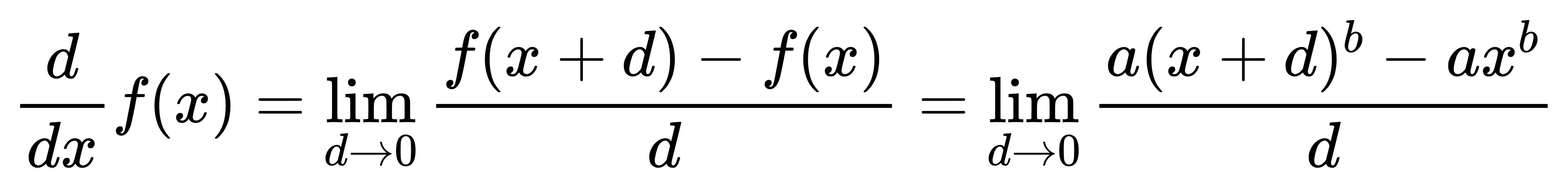
接下來我們只要化簡就好了。
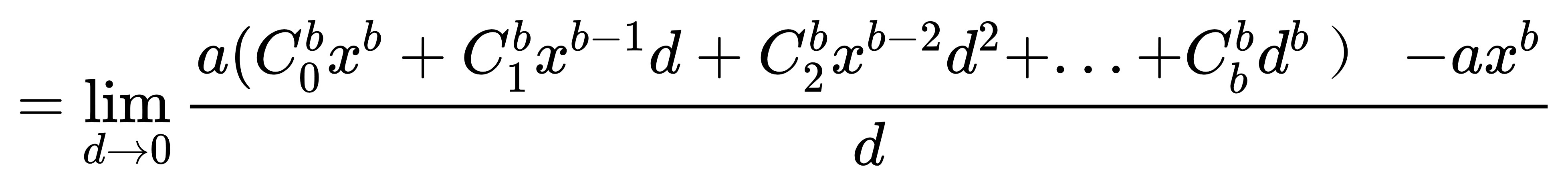
把首項ax^b跟尾項的ax^b互相消掉,
然後殘餘各項把d提出來到括弧外面:
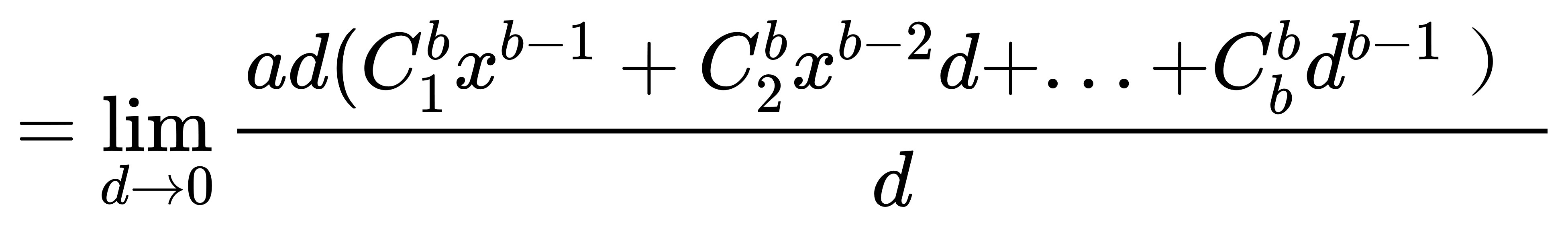
約分後這樣分母就沒有該死的d了。

然後把d→0帶入,
所有帶d的項次通通為0,
因此得到答案:
換句話說,
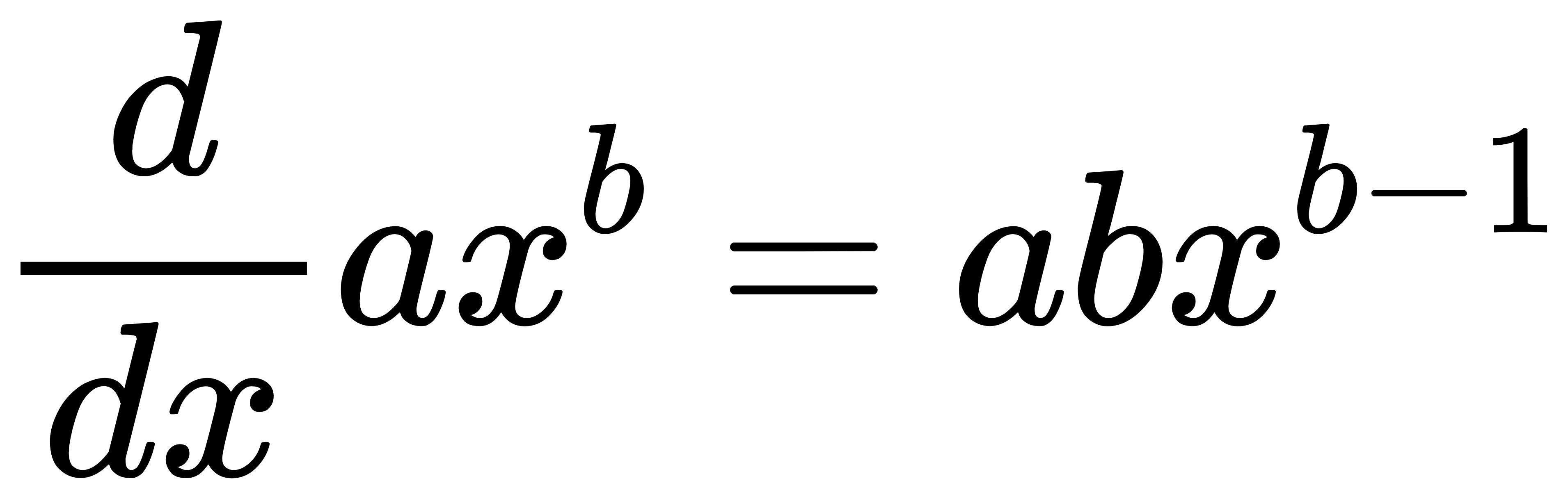
這不就是「指數(b)拿下來當係數,指數減一(b-1)」嗎?
本篇使用的方程式編輯素材來自:LaTeX公式編輯器