達人專欄
你好~ 你說的第一等式，也就是N(ab)=N(a)N(b) a,b 複數，我猜它的其中一項用途應該可以拿來說在Z[i](高斯整環)，是一個Euclidean domain，所以也是principle ideal domain哦~ (所有ideal 在Z[i]環都是由一個元素生成，相當漂亮的結果)
《憂國的莫里亞蒂》中的數學公式
本文來介紹本季動畫《憂國的莫里亞蒂》中出現的數學公式
看看動畫作品中出現的數學，欣賞一下，順便看看內容有沒有錯
在第五話之中，威廉老師在上課時有這麼一個橋段
字真小，拿下面這張清楚了來講
其他部份看不太清楚，就不在本文討論的範圍
(是說板書真工整啊
打清楚一點應該是這樣，暫且稱為「第一等式」
大家可以自己動手算算看，會發現是一樣的，原本想說就只是個代數恆等式，似乎沒什麼意思，頂多就出成一個因式分解的題目罷了
而某天我在看日本的代數書時意外發現這個
出自：代數學 / 淡中忠郎著; 小松勇作等編集
內容大概是從基本的運算性質，講到高深的代數學問
原本這章講的是複數，由這邊切入，意外導出這個式子
有些人應該看得懂是什麼意思，不過我還是解說一下
我們有兩個複數：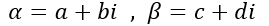
令函數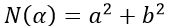
也就是取其複數的實部與虛部平方相加
也就是取其複數的實部與虛部平方相加所以有
以及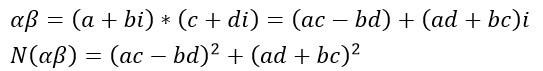
那麼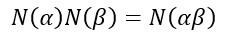
也正是
也正是
你可能會想問這有什麼厲害的，還不跟上面代數的做法一樣？
這邊就是我要講的另外一個觀點了，由複數的觀點切入
一個複數
，其長度為
，其長度為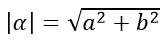那麼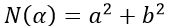就可以看成其複數的長度平方
就可以看成其複數的長度平方所代表的便是：「兩複數長度平方相乘等於兩複數相乘再取長度平方」而兩邊都有平方這個動作，那麼可以化簡
更簡單的來說，就是證明「兩複數取長度後相乘等於兩複數相乘再取長度」
便可間接證明
對複數有點認識的都知道這個，不過還是簡單講解一下：
兩複數分別用極式表示
分別表示兩複數到原點的距離
分別表示兩複數的幅角，便是兩複數與原點連線，與x軸正向與其的夾角兩複數相乘得到
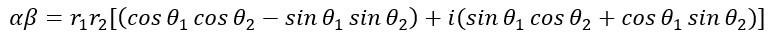
用和角公式化簡有
用和角公式化簡有
這邊已經很明顯了
兩複數取長度後相乘：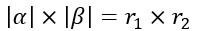
兩複數相乘再取長度：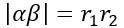
沒錯都一樣
所以我們由「兩複數取長度後相乘等於兩複數相乘再取長度」此一觀點，間接證明了此一等式
最右邊的部分只是將兩複數令為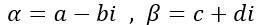
便可得證，可以試試看喔
便可得證，可以試試看喔很不錯吧，不用代數證明，由複數的觀點來看，可以很快的得證這樣的數學式子，當然想不想得到就是另外一回事情了。
而書中的例題1
好吧，要說實用性應該是不高，至少在計算上應該不會幫助太多…
34和74竟然要先看成(3^2+5^2 )和(5^2+7^2 )
再帶入公式中寫成(3×5-5×7)^2+(3×7+5×5)^2
坦白說，我不覺得這樣算會變快，甚至是變慢了... 能夠實際用的場合應該少之又少
遇到兩數相乘我會選擇直接乘或是用乘法公式化簡，應該都是比這個還要更快的作法
兩數都要分別看成兩個整數的平方和，才可應用，使用的時機實在少之又少
再來此圖中下面二式，稱為「第二等式」吧
被遮住了，那比對一下其他角度所看到的
交叉比對下
威廉背後的完整式子應該是這樣：
不過我們把兩邊各自展開會發現...
左式：
右式：
很明顯不一樣，所以這邊是作畫失誤！錯了！
製作組，你們錯了，有看到這篇的話可以修正一下
實際上應該是怎樣才對？
觀察上面的形式，要讓nabcd這一項消去，勢必兩項應該要是一正一負的狀態，往這個方向做調整即可
選擇固定(ac-nbd)^2 ，調整右邊即可
這樣才對
所以完整的「第二等式」應該是這樣：
那要如何應用？
我們舉個簡單的例子：22 x 54 = 1188
22 x 54 = (4+18) x (4+50) = (2^2 + 2x3^2) x (2^2 + 2x5^2)
有a=2 , b=3 , c=2 , d=5 , n=2
可以帶入公式了：
22 x 54=(2x2 - 2x3x5)^2 + 2(2x5+3x2)^2=(-26)^2 + 2x16^2
= 676 + 512 = 1188
沒錯的
很抱歉，跟「第一等式」一樣，實用價值一樣很低
純粹欣賞即可
當然這一樣可以用複數的觀點來解釋
方法一樣，只差在一開始令的兩個複數而已，
實際上還可以推導成：稱為「第三等式」
更一般的形式：
來實際應用看看...
隨意問人，選了兩個數字：247 , 865
那現在就拿這兩數相乘套入此公式，來試試看這公式的威力
確實是一樣的！
不過挺麻煩的就是... 還是直接相乘比較快
兩個整數還要各自湊成兩個平方數的線性組合，才可有下一步，光這邊就花點時間了...
實用程度實在不高，至少我真的覺得不怎麼實用啦，有人覺得這方法很好用那也不錯，
我傾向純粹欣賞即可。
最後總結一下：
第一等式：
第二等式：
第三等式：
一般形式：
(順道一提，文中一直用到的N(ab)=N(a)*N(b) 手法，此一性質可稱為homomorphism
詳情可以去看代數學
兩個群G , H 有個函數N : G→H
存在這樣的映射N(ab)=N(a)*N(b) 對於所有的a,b屬於 G
這樣便是homomorphism
大家有問題嗎？
看完這些還真是辛苦大家了，有問題都歡迎提問
不知道威廉老師當時在教是用何種方式說明的？我查了一下...
《憂國的莫里亞蒂》時空背景大約是19世紀末，1879年威廉已是教授
而現實中，在18世紀1730年已有棣美弗公式、1748年已有歐拉公式
18世紀末已有複數平面的觀點，大多人也可接受，可以說複變開始蓬勃發展
所以以歷史的脈絡來看，威廉老師確實有可能用複數的觀點來教的。
我發去場外，感謝有位叭布的巴友友更深入的說明
數學真的很不錯，由不同的切入點，不同的角度，都能證明一件事情。
我的其他數學文，有興趣可以看看： (當然不是數學的也可以看看)
