感覺樓主很專業(yè)
讓我不確定到底是不是我算錯(cuò)
還是這邊不適用差的平方公式？
讓我不確定到底是不是我算錯(cuò)
還是這邊不適用差的平方公式？
各位好這裡亞夜。
今天在客戶那邊忙了一整天，
晚上沒什麼心情寫稿所以就發(fā)點(diǎn)自己熟悉的東西。
今天要講的是：尺規(guī)作圖開根號。
這裡先簡單的提一下，
數(shù)學(xué)上對於「尺規(guī)作圖」是有嚴(yán)格定義的。
尺規(guī)作圖字面上的意思是只能用直尺與圓規(guī)來畫圖，
但這裡的直尺是沒有刻度的直尺，
因此實(shí)際上就是「只能畫直線跟圓弧」的意思。
因?yàn)闆]有刻度，
所以作圖上的長度只能透過「複製貼上」的方式去執(zhí)行，
也就是說，
必須先給定你一個(gè)線段長，
你才能用尺規(guī)作圖畫出指定長度，
且該長度必然受到該線段長的影響。
好了，
那這裡提到的開根號是什麼意思呢？
是這樣的：
題目必須先給你一段指定長度，
然後你就能畫出該長度的「倍數(shù)」。
如果這個(gè)倍數(shù)是「有理數(shù)」那好辦，
原因很簡單，
利用尺規(guī)作圖，
要把指定長度延長整數(shù)倍，
或等分為整數(shù)倍都是易如反掌的事情，
而有理數(shù)就是「能寫作兩個(gè)整數(shù)相除的數(shù)」，
換句話說，
這個(gè)倍數(shù)必然可以寫成m/n的形式且m、n都是整數(shù)，
那我們就能夠透過延長m倍並等分成n等份的方式來取值。
可是，
當(dāng)這個(gè)倍數(shù)是「無理數(shù)」時(shí)怎辦？
如果這個(gè)無理數(shù)是某個(gè)有理數(shù)的「平方根」，
那尺規(guī)作圖就作得出來了，
這就是今天敝人要講的。
重申一次，
尺規(guī)作圖的先決條件是必須給定一個(gè)指定長度。
不管這個(gè)長度是多少都無所謂，
但總之必須以這個(gè)長度為基準(zhǔn)，
否則以下內(nèi)容都是雞講的。
OK回到正題。
給定一條線段長a，
請問如何畫出現(xiàn)段長為「a的根號2倍」的長度呢？
這個(gè)很簡單：
利用《商高定理》（或曰：《勾股定理》、《畢氏定理》）即可。
《商高定理》的基本內(nèi)容是：
給定一個(gè)任意直角三角形，
其兩股之平方和必然等於斜邊的平方。
我們可以把這個(gè)定理寫成：
x^2 + y^2 = z^2
當(dāng)中，x≦y<z，且x,y,z為直角三角形的三邊長。
那到這裡應(yīng)該很簡單了吧？
只要令x=y=a，
那z就是(√2)a了。
這裡只是簡單的√2倍，
那有沒有一個(gè)通式，
可以「令根號下任一倍數(shù)」都能畫出來呢？
其實(shí)還挺簡單的。
當(dāng)然：前題根號下必須是有理數(shù)，如果根號下是π還是?之類的當(dāng)然還是沒辦法的。
要作通式，
那我們只能假設(shè)題目是求畫出a的√(m/n)倍了，
其中m、n都必須是正整數(shù)。
哼哼，
這個(gè)簡單。
我們先討論m=n的情況。
m=n，
那就是1倍。
1倍還畫個(gè)毛線啊，
直接複製線段長就完事了對吧！
接著討論m>n的情況。
m>n意味著這條線段必然比a長。
這個(gè)就簡單，
我們先找出(m-n)倍的a。
這不難，
因?yàn)檫@裡規(guī)定了m、n都是正整數(shù)，
因此一定算得出m-n，
也因此我們一定能畫出一條長度是(m-n)倍a的長度線段。
接著我們再把這個(gè)線段n等份，
我們就得到了(m-n)/n倍a的長度的線段。
我們也可以說這條線段的長度是[(m/n)-1]倍a的長度，
方便起見，
我們叫它b。
現(xiàn)在，
用a線段跟b線段作直角三角形的兩股，
尺規(guī)作圖畫直角是基本功，
這裡就不解釋了。
接著連接出斜邊，
斜邊長度就是a的√(m/n)倍了。
證明：
a邊平方＝a^2
b邊平方＝{[(m/n)-1]a}^2=[(m/n)a]^2-a^2
斜邊平方＝上兩式相加＝[(m/n)a]^2得解
舉例來說，
我們要畫出a的√(7/3)倍，
那麼就先畫出b=4/3倍的a，
再用a跟b作兩股畫斜邊。
那麼m<n呢？
這個(gè)就稍微比較難一點(diǎn)了，
這涉及到「分母有理化」。√(m/n)
=√m / √n （先相除再開根號＝先個(gè)別開根號再相除）
=√mn / n （分子分母同乘以一個(gè)數(shù)）
因?yàn)閙n都是正整數(shù)，
所以可以算出數(shù)字。
接著利用上面的方法先化出√mn倍的a，
接著再把這個(gè)線段做n等份就得解了。
例如，
我們要畫出a的√(2/3)倍，
那就是先畫出a的√6倍然後再三等份即可。
喔對了，
能不能畫√a呢？
答案是：不能。
a是單位長度，
它的概念並不是一個(gè)數(shù)字，
而是單位。
你把單位做平方或開根，
它就不是原本的單位了。
就像10的平方是100這很好理解，
但10公分的平方是100平方公分，
10公分是長度，
但100平方公分是面積而不是長度，
你無法畫出一個(gè)100平方公分長的線段，
懂嗎？
我們現(xiàn)在確定了，
給你一個(gè)單位長度a，
你就能畫出任意有理數(shù)，或帶根號倍的a的長度的線段。
那現(xiàn)在給你兩個(gè)線段長a、b，
能不能畫出長度是√ab的線段呢？
我們剛剛說，
給定a的情況下√a畫不出來的，
那麼想當(dāng)然耳給定b的情況下√b也畫不出來。
既然√a跟√b都畫不出來，
那麼√ab當(dāng)然也畫不出來。
才怪。
事情才沒這麼單純。
√a畫不出來的理由是什麼？
舉例來說，
假設(shè)a是9公分，
√a就是3根號公分。
根號公分是什麼單位？
先不管，
反正它不是長度單位就對了，
所以畫不出來。
同理假設(shè)b是16公分，
那√b就是4根號公分，
因此也畫不出來，
到這裡沒有問題。
那√ab就是3根號公分乘以4根號公分等於12公分。
有木有！
√ab竟然是長度單位！
既然是長度單位，
那當(dāng)然畫得出來呀！
那具體怎麼操作呢？
我們可以這樣做：
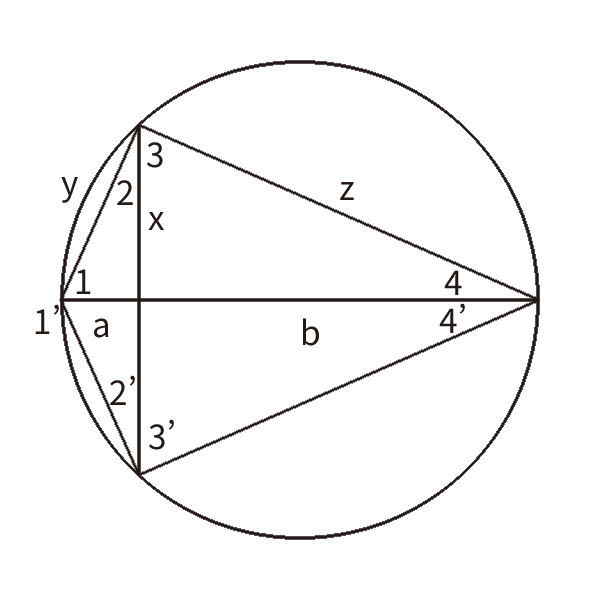
１、首先先畫一條線段，長度等於a+b，我們假設(shè)這條線段為c
２、以c為直徑作圓。
３、在線段c上，以通過ab線段交點(diǎn)的位置作垂直線，令這條垂直線穿過圓周。我們令這條線為直線d
４、直線d上介於線段c與圓周之間的這段線段即為所求。
證明：
線段c=線段a+線段b，
以線段c為直徑作圓。
∵角4與角2'具有相同的圓周，
∴角4=角2'
又中間兩條直線垂直，
根據(jù)等腰三角形底角相等性質(zhì)，
角2=角2'，
∴角4=角2
同理可證：角1=角3
∵角1=角3且角2=角4
∴△axy與△xbz相似
∴x/a = b/x（相似三角形兩對應(yīng)邊比值相等）
＝＞ab=x^2
∴x=√ab得證
延伸：
給你a跟b求畫√ab很簡單，
那給你a、b、c求畫?abc呢？
答案是：畫不出來。
雖然?abc的單位依然是長度單位，
但是尺規(guī)作圖無法繪製立方根，
因此此題就真的無解了。
【後記】
亞夜愛數(shù)學(xué)。
封面圖片：《武裝神姬》聖誕、賽連、人魚的三角含術(shù)
等等，
尺規(guī)作圖乾三角函數(shù)屁事啊？
達(dá)人
