本文算式圖片設計以深色模式為主,閱覽前建議切換為深色模式。由於手機 App 在切換樣式前需要強制重啟 App,若你是日間模式使用者,請在切換前利用「收藏」功能,避免切換完模式以後找不回本文。
在微分的基本技巧當中,對數微分法可以算是一系列方法裡的最後一種。其實關於微分的應用還有很多東西可以講(譬如全微分、線性近似),不過並不是每個科系的學生都會需要用到,等講完對數微分法以後就直接講積分吧,剩下的東西之後再說。
上次說明對數(log、ln)的時候,我們提到過:凡是不好處理的指數,只要使用對數函數就可以把指數提到函數外面,成為係數:
在處理複雜的微分問題的時候,我們一樣可以利用對數來簡化它。上次介紹過「e」這個常數的特殊性質,所以在微積分領域當中,最好用的應該會是 ln 而不是 log。
可以想像,既然今天使用對數來簡化算式裡的項目,那麼總會有很大的機率遇上「需要把 ln x 對 x 微分」的情況。為了先準備好未來可能會用到的工具,我們試著求求看 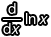 吧!
吧!
。ln x 的微分
學到對數函數微分的時候,我們會很常需要用到這兩個公式:
(上次講對數函數的時候提過)
ln x 算是一個比較特殊的函數。我們想證明 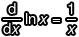 ,要是直接套用定義的話:
,要是直接套用定義的話:
你會發現最後出來的東西很複雜。雖然繼續做下去確實可以直接利用 e 的定義來得到結果,但我相信你不會想這麼做的。
我們可以利用 ln 函數的本質 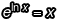 拐個角來嘗試:
拐個角來嘗試:
成功了!這就是利用微分連鎖律來證明 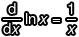 的過程。使用微分連鎖律的時候一定要注意分母標示的微分對象是誰,不然你會看不懂這個過程怎麼來的,這個當時再三強調過,千萬不可以搞混。
的過程。使用微分連鎖律的時候一定要注意分母標示的微分對象是誰,不然你會看不懂這個過程怎麼來的,這個當時再三強調過,千萬不可以搞混。
。有了這樣的工具,就能用來應付複雜的函數
假設今天有一個函數:
直接利用除法律和乘法律的話,雖然也不是無法達成目的,但肯定比較麻煩。我們直接利用對數可以「化指數為乘法、化乘除為加減」的特性,把它拆下來,然後經過微分連鎖律拆成該拆的項目,再移項一下就可以得到結果:
這個看起來稍微複雜一點。實際上,我們只是把先前曾經提過的各種規律混合起來做而已,遇到什麼就使用什麼:
log(AB) = log A + log B
看不懂過程的話,我們拿 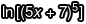 對 x 的微分過程來分解動作,可以注意到我們只不過是運用了上面的幾種規律而已,其他都是比照辦理:
對 x 的微分過程來分解動作,可以注意到我們只不過是運用了上面的幾種規律而已,其他都是比照辦理:
ln y 對 x 微分也同理,因為我們知道 ln y 對 y 微分的結果是  ,套用到微分連鎖律就可以得到:
,套用到微分連鎖律就可以得到:
它的主要原理就是因為使用對數、套用連鎖律的時候恰好會多一個 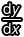 出來,所以我們只要經過整理,就可以得到我們想要的
出來,所以我們只要經過整理,就可以得到我們想要的 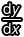 ,同時又具備把指數化簡運算的功能。
,同時又具備把指數化簡運算的功能。
。x 的 x 次方,怎麼微分?
這也是個經典題。我們剛開始在學微分的時候學過最基本的規律:
但這僅限於指數是常數的情況下。你可以想像一下,當 x 在變動的時候,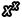 無論是底數還是指數都在跟著移動,想當然爾,這就跟
無論是底數還是指數都在跟著移動,想當然爾,這就跟 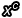 (C 為常數)完全不可比擬。即使直接使用微分的基本定義(令 Δx → 0)來求取導函數,你也不會得到
(C 為常數)完全不可比擬。即使直接使用微分的基本定義(令 Δx → 0)來求取導函數,你也不會得到 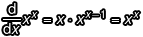 這樣的結果。
這樣的結果。
簡單來說:如果你認為 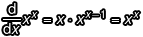 的話,那你就太天真了,因為這樣的想法從根本上來看就已經有問題,自然不能通用。
的話,那你就太天真了,因為這樣的想法從根本上來看就已經有問題,自然不能通用。
這種情況下,我們一樣使用對數微分法來處理:
還是一樣老概念,遇到嵌套兩層的項,就使用連鎖律;遇到相乘的組合項,就使用乘法律,只要整理一下把 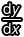 整理到一邊,就得到我們想要的了。
整理到一邊,就得到我們想要的了。
我們甚至可以在「知道 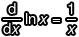 」的前提下,利用對數微分法推出
」的前提下,利用對數微分法推出 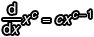 :
:
因為「常數」的英文是 constant,所以習慣上我們會用它的字首 C 來表示一個常數。
當然,只要想法是對的,無論你是用正規的做法還是對數微分法,得到的結論都會是相同的,只是我們使用了不同的方法去達成目的而已。總而言之,只要遇到麻煩的指數問題,用對數就可以去解決它。
如果還要嚴謹一點的話,可以把 ln 裡面的真數加上絕對值(比如把 ln x 記為 ln |x|),規避真數小於 0 而導致 ln 無意義的情況。
對數微分法大概就是這樣了,接下來的期中考就請大家好好加油吧。