題目都一樣，所以這裡一起解說

首先是階乘的定義：設一個正整數 n ，符號 n！代表從1開始依正整數順序連乘到 n

即 n！= 1 x 2 x 3 x ...... x n，而為了計算上的方便，定義 0！= 1，接著就是題目所要求的，給定一正整數 n，求 n！當中從個位數起算，第一個遇到的非零位的數字為何？例如 n = 10，10！= 3628800，從個位數往前找，第一個非零位數字是 8，很顯然的，解題不可能使用暴力法直接連乘，因為題目測資非常非常大，將測資給定的數字使用階乘，會遠遠超過一般存儲數字的上限，因此必須改以「找規律」的方式解題。(題外話，大部分題目都是要找規律)

這裡不妨先思考題目要求的 "第一個非零位數字"，階乘是從 1 開始連續一段自然數相乘，2！、3！、4！尾端都沒有 0，從 5！開始就出現第一個 0，而第二個 0 是要到 10！才出現，尾端的 0 代表 10 倍，而

10 = 2 x 5，也就是說 n！尾端有幾個 0，就代表將 n！質因數分解後，質因數 5 的次方數，而在有限大的 n 以內，是 2 的倍數的自然數一定比是 5 的倍數的自然數多，因此 n！內所有的 5 都與 2 相乘變成了尾端的 0，也就是說尾數是 5 的自然數不會影響第一個非零位。因此我們可以令 n！= 2^a * 5^b * c，其中

a、b、c都是整數且 c 與 2、5 互質，由剛剛的推理可以知道 5 不影響尾數變化，那麼剩下的部分

2^(a-b) * c，就是造成尾數變化的原因。

尾數變化看似雜亂無章，但如果我們把相同尾數的質因數看作一個群體，觀察相同尾數相乘之後的樣子，

或許可以找到一些規律，以下是 1 ~ 9 的次方數表格：

從指數中觀察規律：

(一) 1 不論怎麼乘都是 1，所以尾數是 1 的質因數 ( 11、31、41... ) 不影響 n！第一個非零位數字

(二) n！在質因數分解之後，除了 2 其他質因數都是奇數，所以原本尾數4、6、8的自然數都不需考慮，

       僅僅只考慮 2 即可

(三) 5 不影響非零位，上面已經解釋了

(四) 觀察 2、3、7、9 次方的尾數，能明顯發現 2、3 跟 7 每 4 個循環一次，9 每 2 個循環一次：

       (1) 2 的循環節：2 > 4 > 8 > 6

       (2) 3 的循環節：3 > 9 > 7 > 1

       (3) 7 的循環節：7 > 9 > 3 > 1

       (4) 9 的循環節：9 > 1

       不論題目測資有多大，我們都不需要去逐一列出每個質數後再分析尾數，而是直接將相同尾數看作一個群體，直接算這群體含有幾個數字，將 n！轉化成 ( 尾數 ) ^ (個數)，再利用循環節就能快速求解了。

我們知道 9 = 3^2，代表說乘一次尾數 9 的結果會等價於乘兩次尾數 3，然後觀察 3 跟 7 的循環節，運用一點技巧我們得知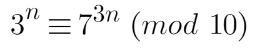( n 是自然數 )，這裡使用了 "同餘" 的概念，

同餘簡單說就是在三等號的左右兩邊的數字，在分別除以同一個數字後會有相同的餘數，這式子用術語來講就是 " 3^n 與 7^(3n) 對模 10 同餘 "，某數除以10 的餘數恰好是某數的最後一位數字，運用技巧做出來的上述式子是為了讓 3 與 7 的循環節內容一致，從而使乘一次尾數 3 的結果會等價於乘三次尾數 7 ( 可以自己手動帶入 n 的值，用上面的表去對照 )，我們就成功將影響 n！第一個非零位的數字壓縮到剩下 2 跟 7 了。

綜上所述，我們在 1 ~ n 之間，針對每一個正整數提出全部的 2 跟 5 後，在剩餘部分裡分別統計尾數 3、7、9 出現次數，然後利用 "同餘" 的概念，快速解出多個2、3、7、9 自乘後的尾數為何，最後相乘取其尾數即得到答案。

用文字敘述實在非常難解釋解題的思路，以下直接使用範例 123！，來求題目要求的答案：

(一) 首先是處理 5，統計一個階乘能分解幾個 5，只要算這一連續的自然數當中有幾個 5 的倍數就好，

       1 ~ 123 中有幾個 5 的倍數，很簡單，回憶除法的最初始定義，將 1~123 依自然順序每 5 個為一組，

       1~5、6~10、......、116~120、121~123，一共有123 / 5 = 24 組 ( 餘數在程式運算過程會自動捨棄 )

       這 24 組中都恰好只有一個數字是 5 的倍數，但我們知道這些數字當中還有 5 的倍數，於是我們將這

       24 組中的 5 的倍數拿出來，依自然順序再分組，一共有 24 / 5 = 4 組，意思是 24個 5的倍數中，

       還有 4個能再提出一個 5 出來的數字，也就是 25、50、75、100，下面用圖表來說明這一段：

       在第二次分組中能發現，數字在提出 5 之後，尾數發生了改變，由先前提到的我們只關注尾數是 2、

       3、7、9 (偶數部分暫不處理) 的部分，但是在提出 5 的過程中這些數字才出現，代表在統計 5的倍數

       過程能一併統計尾數 3、7、9的數字有多少，除了 5 的倍數，還有 2 的倍數需要處理，但有數字既是

       2 的倍數也是 5 的倍數，這裡我們寫程式只要使用雙重迴圈就可以解決。分組只要進行 2 次就能得到

       123！中一共有 24+4 = 28 個 5 連乘，2 的倍數也是同樣的方法，可以得到

       別忘了在程式中除法會自動刪除無法除盡的餘數，所以我們知道 123！中有 117 個 2 連乘，寫成數學

       式 : 123！= 2^117 * 5^28 * c，接著就是統計尾數 3、7、9的數字了。

(二) 尾數 3、7、9的數字該怎麼統計呢，一樣以範例 123！來分析，我們現在使用的數字是 10 進位，從

       自然數 1 開始一個一個數，數到十後數字會寫成 10，這些數字當中，尾數 3、7、9 數字都恰只出現

       一次，接著從 11 數到 20，尾數 3、7、9 數字同樣恰只出現一次 (13、17、19 )，依此類推一直到

       121 ~ 123，此時只有尾數 3 數字 123 而沒有尾數 7、9，因此我們統計出尾數 3 數字出現了

       3、13、23、......、113、123 共 12 + 1 = 13 個，尾數 7、9 則各 12 個，前面說過我們不需要在意

       這個數字的全貌，只在意個位數就好，因此我們就把 (一) 結尾的 c 直接看成 3^x * 7^y * 9^z，因此

       到目前統計 x = 13，y = z = 12。接下來要提出 2 跟 5 繼續統計，以下用圖表表示：

       經過完整分析之後，尾數 3 的數字有 33 個，尾數 7 的數字有 26 個，尾數 9 的數字有 25 個，於是

       我們的 c 就可以改寫成 3^33 * 7^26 * 9^25。

(三) 由(一)(二)我們將 123！改寫成 2^117 * 5^28 * 3^33 * 7^26 * 9^25，首先每一個 5 能與一個 2 相乘，

       變成123！尾端的 0，消去所有的 5 後剩下 2^89 * 3^33 * 7^26 * 9^25，接著因為循環節，可以得知

       89 ≡ 1 (mod 4)，也就是 2^89 ≡ 2^1 (mod 10)，然後 9^25 = 3^50，則尾數 3 有 33+50 = 83 個，再

       接著 3^83 ≡ 7^(3*83) (mod 10)，則尾數 7 有 26+83*3 = 275 個，觀察尾數 7 的循環( 對照上面 )，

       275 ≡ 3(mod 4)，也就是 7^275 ≡ 7^3 ≡ 3 ( mod 10 )，最終可得123！≡ 2*3  ≡ 6 ( mod 10 )，因此

       123！的第一個非零位數字是 6。演算過程如下：

至此，我們能使用這方法對任意大的自然數 n 的階乘 ( n！) 求第一個非零位數字，最後附上我的程式碼

----------------------------------------------------------------------------------------------------------------------------------------