此題的解題動態已有公式，大部分人應該直接套公式解題
但我猜大部分人都不知道公式是怎麼推導出來的 (解題動態那個不算推導 )
這邊是我觀察規律，在網路上找參考資料之後推導出公式的過程 :
由題目敘述已知初始狀態為從 1 ~ n 的連續正整數排成一列
每進行一次操作，就把該列相鄰兩數字兩兩相加，這邊不妨將過程倒過來看
n = 1，答案就是 1，不用處理
n = 2，如圖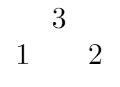 
，最下層是初始狀態，上一層是下層相鄰兩數的和
，最下層是初始狀態，上一層是下層相鄰兩數的和n = 3，如圖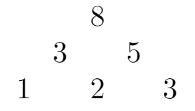
n = 4，如圖
，這邊或許有些人能看出來某種規律了
，這邊或許有些人能看出來某種規律了n = 5，如圖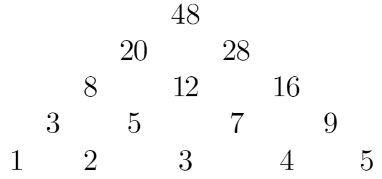
，
，數學上有某個三角形，上層相鄰兩數的和等於下層數字，就是「巴斯卡三角形」
雖然跟這題是上下相反的，但重點是巴斯卡三角形的數字恰好可以與這三角型的數字一一對應
右圖是5層的巴斯卡三角形 
在二項式定理中，巴斯卡三角形每一層代表該層的二項式展開後的係數
如第3層是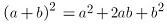
對應係數就是 1、2、1
對應係數就是 1、2、1接著我們把題目 n = 3 情況拿出來看，已知 3 = 1 + 2，5 = 2 + 3
那麼 8 = 3 + 5 = ( 1 + 2 ) + ( 2 + 3 ) = 1 x1 + 2 x2 + 1 x3，有沒有發現數字剛好跟巴斯卡三角形一一對應
再看 n = 4，由上面可以知道 12 = 1 x2 + 2 x3 + 1 x4
那麼 20 = 8 + 12 = 1 x1 + 3 x2 + 3 x3 + 1 x4
n = 5 時，48 = 20 + 28 = 1 x1 + 4 x2 + 6 x3 + 4 x4 + 1 x5
由上述規律可以將這題寫成一般式如下 :
題目要求的整數 n，操作完後可以寫成
接下來的目標就是將上面的表達式轉換成公式，這邊會用到一些組合數的一些規律
(一)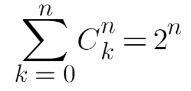
，(二)
，(二)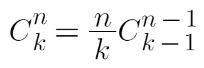(一)證明很簡單，二項式定理中，( a+b )^n 中令 a = b = 1 即可；
(二)也很簡單，由組合數定義以階乘展開，從中提出 n / k 即可
則此題表達式轉換如下 :
其中第2行的 k = 0 變成 k = 1，因為 k = 0 時求和展開的第一項是 0，既然是零那 k 就直接從1開始
第3行中原本 k = 1 ~ n-1，代入組合數後會發現實際上 k 從 0 開始數到 n-2，所以修改其上下標變成第4行
記得如果 k 的上下標有修改，每一項含有 k 的式子也會更改
最後一行就是本題的答案了
有意思的是如果 n = 1 代入公式後會得到 1，與答案依然符合，不過解程式題中整數值遇到除法會涉及浮點數計算，為了避免建議還是加個簡單判斷去除 n = 1 的情況
而這題需要使用大數運算，因為 2 的次方一下子就突破語言中一般基本型態的上限了
以上就是本題的個人思路歷程。
達人
