意想不到的神秘的角度問題
本文在討論上圖這個角度問題
最先是有人詢問我,本以為是稍難的角度問題,給我幾分鐘便可解決,沒想到一做下去,不得了,確實是難題。還比常見的角度難題更複雜(經典的20度問題) 便激起我的興致。
大家不妨嘗試看看,下面就要開始解說囉,不想看答案的趕快自己想,不要下拉
準備好了嗎?
大部分人可以很快發現此大三角形三角分別為48°-66°-66°
因此必為等腰三角形,然而關於所求的x還是不知。原本想說用正弦定理,但列出的式子醜到不行,基本上無能力解,而純幾何的作法更是想不透,只能亂猜測角度,最後使用軟體測量出角度,確定真相。
(所求為上圖的角BCP)
使用GGB做出此三角形,直接量測角度,所求角度是42度,那麼是否有合理的解釋呢?又不借用電腦軟體的幫助,又如何自己得知呢?
以下將分享自己找到的四種做法:(有些是自己想到,有些是別人提供,都會註明)
1.輔助線法:
此方法為在FB的數學社團所看到,由厲害的高手-「鍾昭旭老師」所分享,(已徵得對方同意)
此做法非常厲害,值得好好欣賞
做輔助線:
(1)做正三角形?ABD,如下圖藍色三角形
(2)做等腰三角形?ABE,如下圖橘色三角形
(3) 以 ??點為圓心, ??????為半徑畫圓
(4) 連接 ????? ,????
(5) 以E點為圓心,(EA) ?為半徑畫圓,並以E點為中心點做正五邊形ABFGH
確實做出來了,非常厲害的輔助線法
實在是難以想到,佩服想到這招的高手
2. 三角關係式
學過高中數學,可使用正弦定理(或是其他方法) 列出許多關係式,然而由於角度的關係,基本上是難以解下去的
在此提供一個較為簡單的做法:
接著嘗試解看看此方程式
基本上要解此三角函數方程式是非常困難的,雖然這些正弦值有辦法以根式表示,但會非常複雜,複雜到難以化簡,更別說解出來了
使用特別的化簡方法,必須利用:
實際上還有一個解:??=????°+??????°=??????°,以及這些同位角都符合
不過這不符題意因此不考慮
3. 過外心法
先說這算是比較投機的作法,如果並非這題的特殊狀況,可能不適用
也是我自己想到的做法
如下圖所示,必須去驗證:延伸 ?????是否也會過之外心 ??,如果是,這題將非常簡單
4.應用定理
此方法為巴友 (風吹翊影)所提供,在日本網站上找到的做法
在此推薦:おおせきの部屋 http://azuki2018.html.xdomain.jp/kakudo.html
此網站收錄了一系列類似的困難角度問題,有興趣不妨參考看看
也將做法詳細附上,值得好好欣賞
直接分享網站上的檔案,(如有問題還請告知,這邊僅作為分享作法之用)
以下作為解說
網站上收錄的題目,圖非常的簡單漂亮
必須先引用此定理 限定在圓內接六邊形才可使用,且對角線皆過一點P
此定理的證明過程如下,其實就是利用相似形的概念,並不難
可以算是西瓦定理的推廣
接著就可以開始做了:
此做法非常高明,再此解說一下
先做三角形的外接圓,並構造一個圓內接六邊形AFBDCE
接著利用定理證明三條對角線交於P點,即得到所求角度
中間那一長串的計算結果,就是再利用定理去做驗證
最終得出 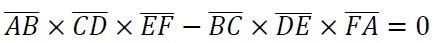
才可以說三線交於P點,(由它的定理) 才可以算出角度
(過程用到積化和差、三倍角公式、 sin18°等 )
此作法相當厲害,看完理解完實在覺得漂亮且奇特到不行,甚至是根本想不到(為何選用這個定理?為何知道要這樣構造?背後是想了多少?下了多少功夫才想到的?),很厲害的活用了此定理。佩服這樣的巧思,想到這招的人必定是個高手!
四個做法中,只有第一個做法算是純幾何的,其餘皆有使用三角關係式(或是說三角函數),二與三作法則是自己想到的,作法四則是讓我認識到許多厲害作法。我相信應該有其他做法的,數學之路條條大路接通!不限定任何作法,這才是數學的自由
還有人有什麼其他做法也都可提供出來討論!
你看懂了嗎?
之前寫的數學文章也歡迎看看: