這裡是亞夜。
5年前敝人寫了一篇數(shù)獨教學(xué),
不過那篇引用了句有重解的數(shù)獨題,
因此到最後出現(xiàn)得瞎猜的情況,
算是挺遺憾的。
5年後的現(xiàn)在,
敝人裝了比較優(yōu)秀的數(shù)獨阿鋪哩了,
因此這次就能介紹一下正手了。
例題:
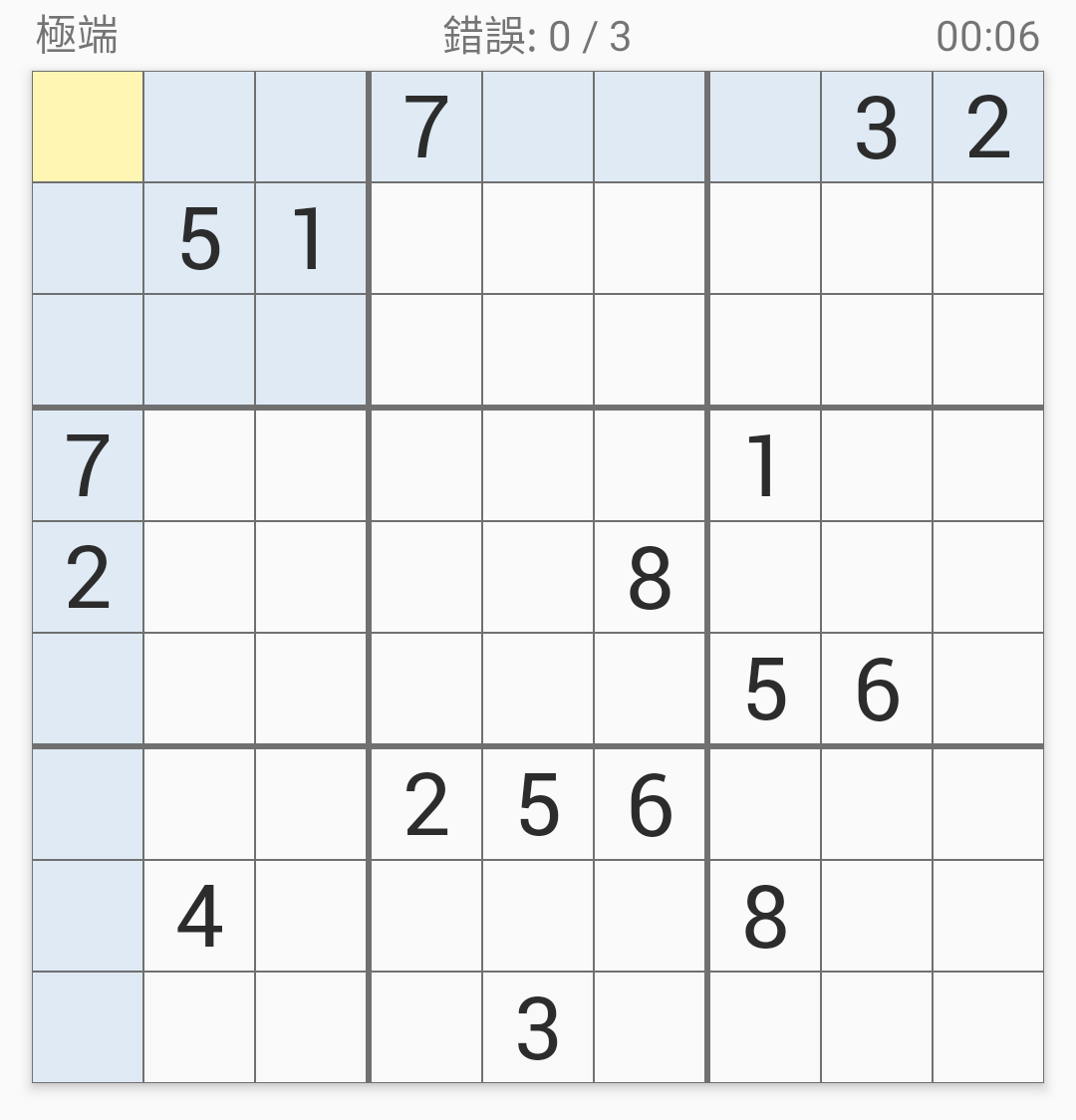
首先,
當(dāng)然是先做筆記。
請參考上一篇的做法,
將候選數(shù)填滿每一個格子:
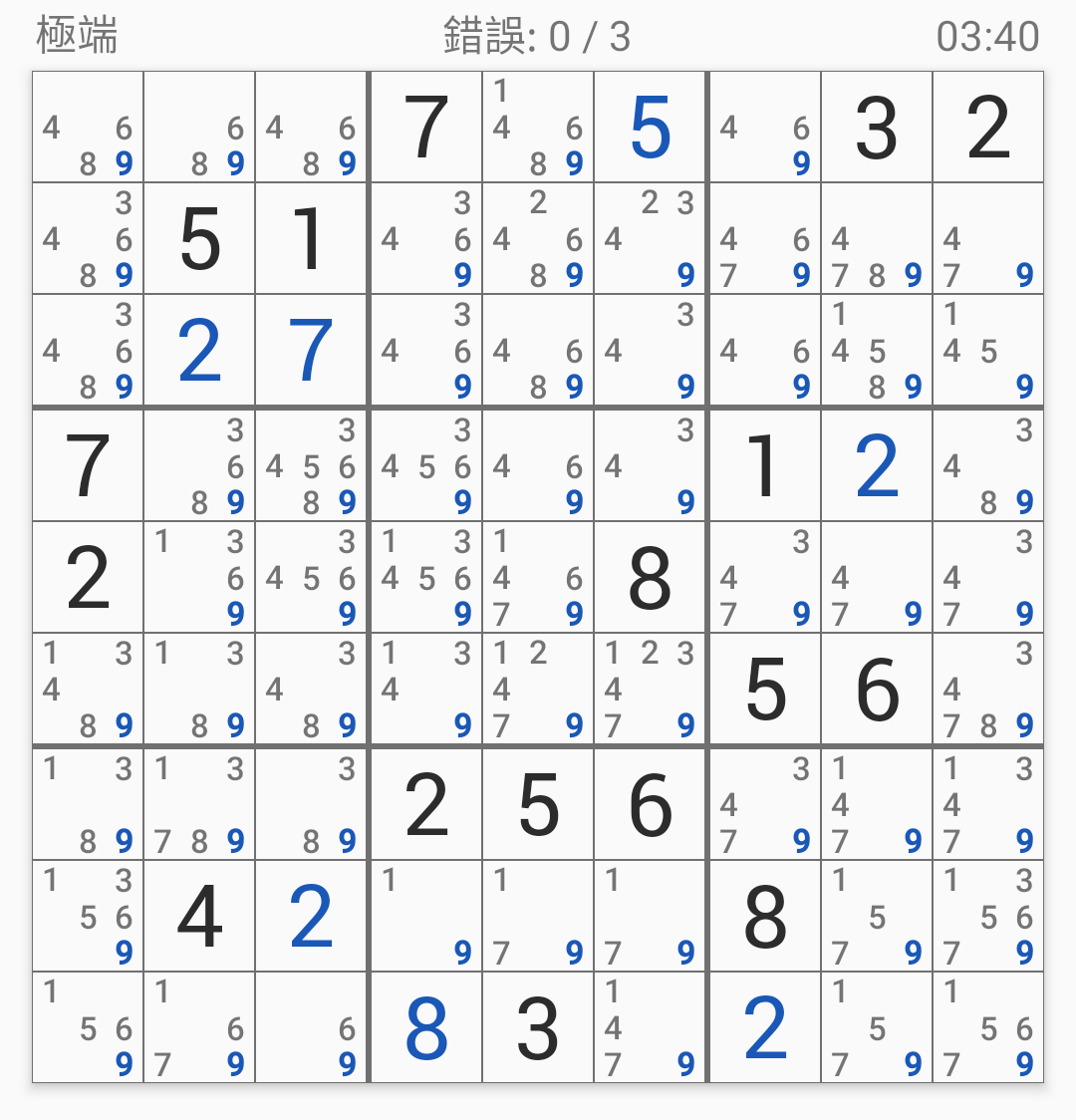
花了3分多鐘總算填完了。
當(dāng)中如果有可以直接確定位置的格子就順手補起來了不用浪費時間。
這個題目裡一個9都沒有出現(xiàn),
像這種有缺數(shù)字的題目整體是比較麻煩的,
不過請放心,
如果一道數(shù)獨題裡面缺2種數(shù)字那就一定有重解(因為一定是兩種數(shù)字對調(diào)也可以對吧?),
因此最多也只會缺1種數(shù)字而已。
接下來就是考驗觀察力了:
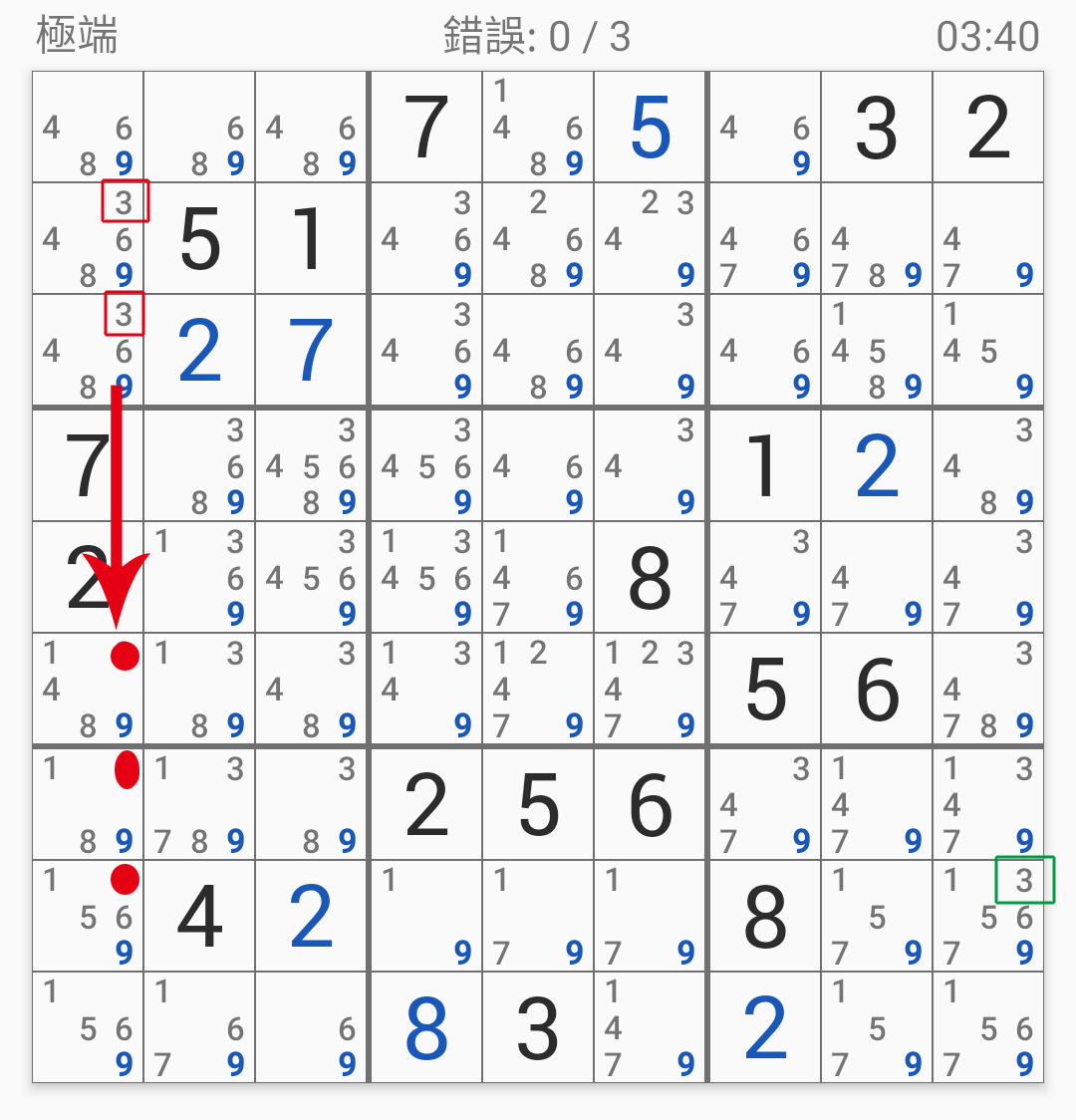
第一宮的3雖然無法確定位置,
但可以保證只會位於第一列。
既然第一列的3必須在第一宮,
那麼第八行的第一格就不能是3,
因此第八行的3必須在第九格。
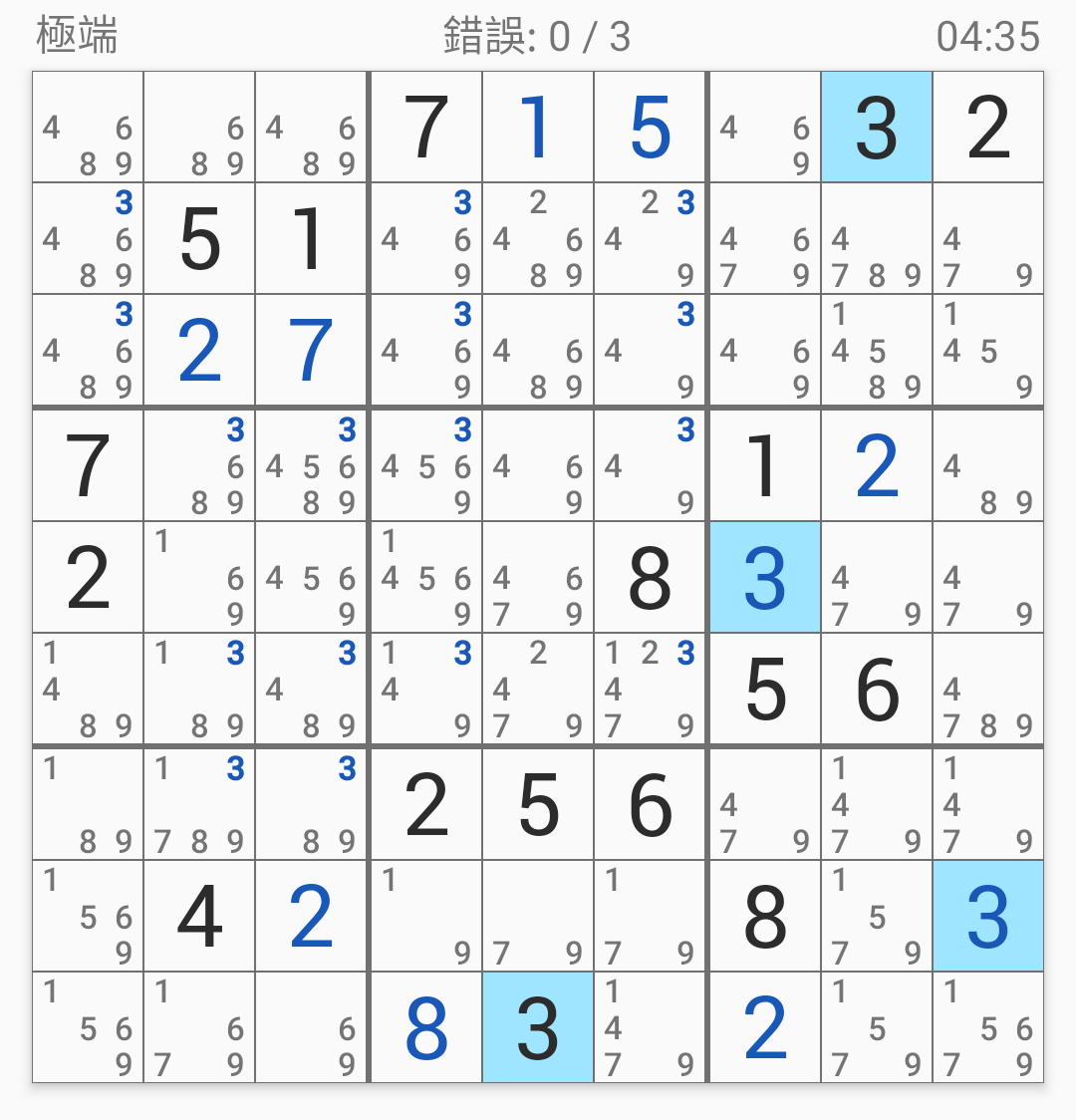
然後就順便把能確定的都給填了。
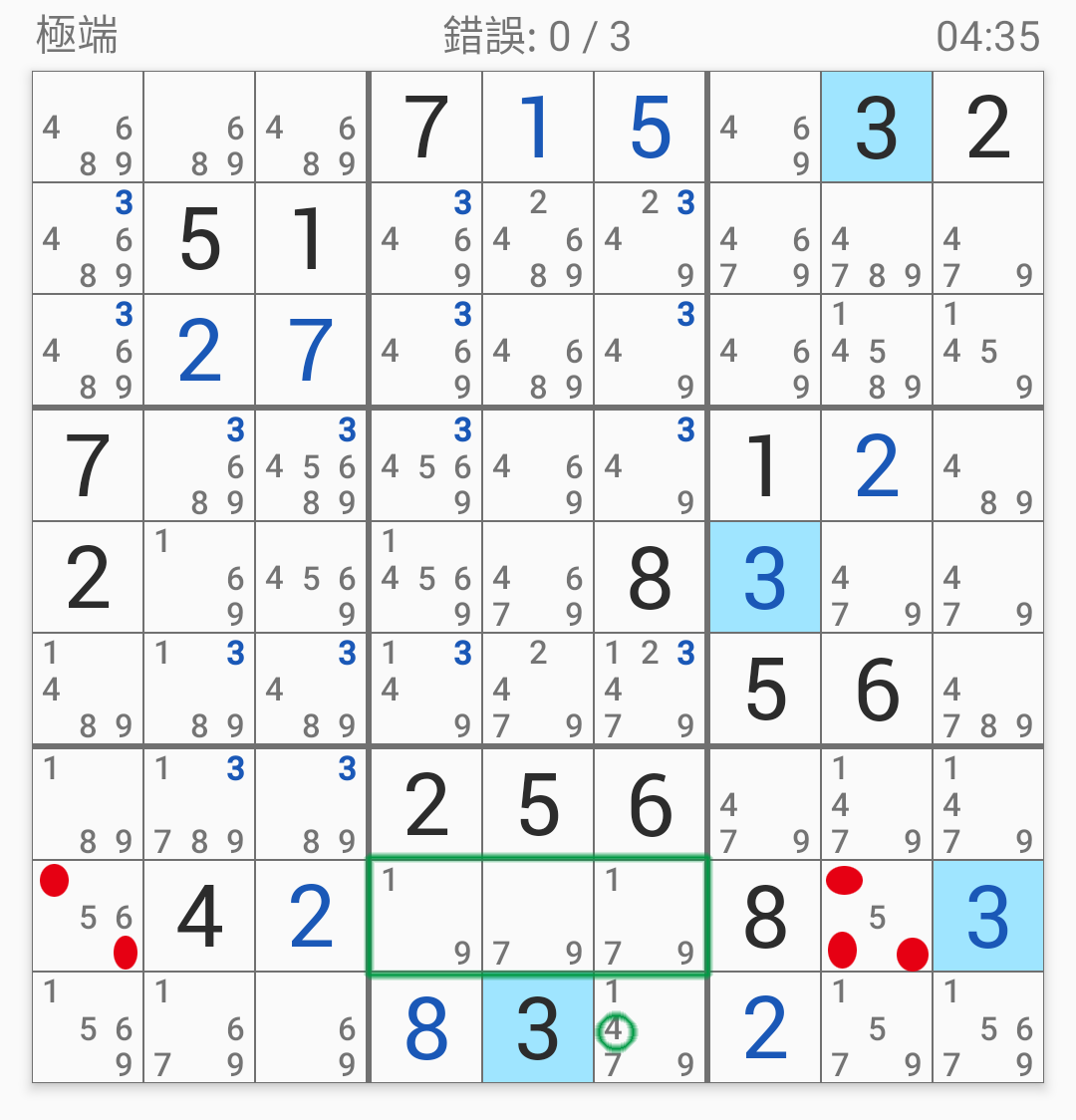
接著注意到第八宮,
4只能在第九格,
因此第八宮跟第八行交集的地方必然是179。
那麼第八行其他格子就能排除掉179,
因此馬上就能確定56的位置了。
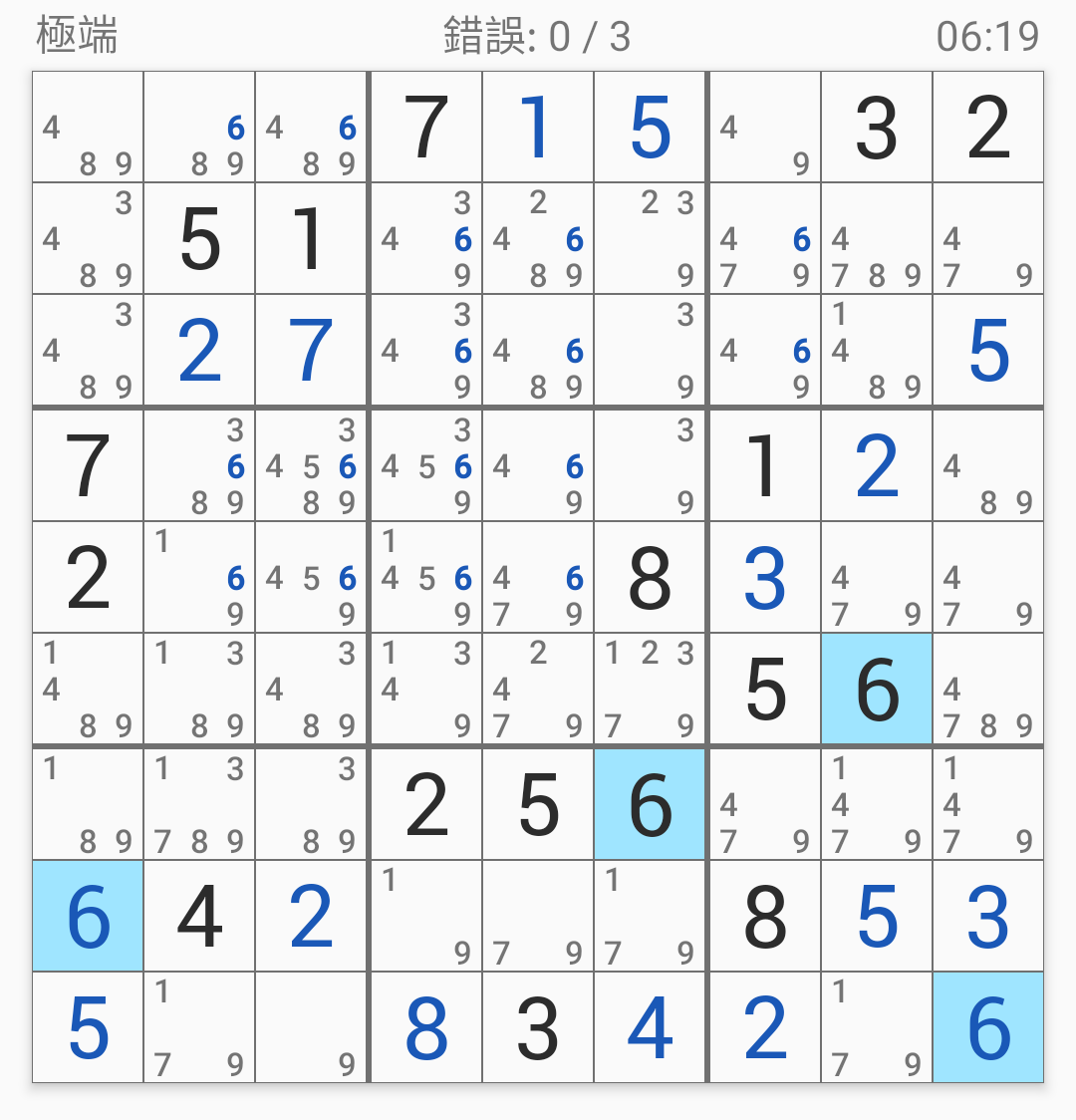
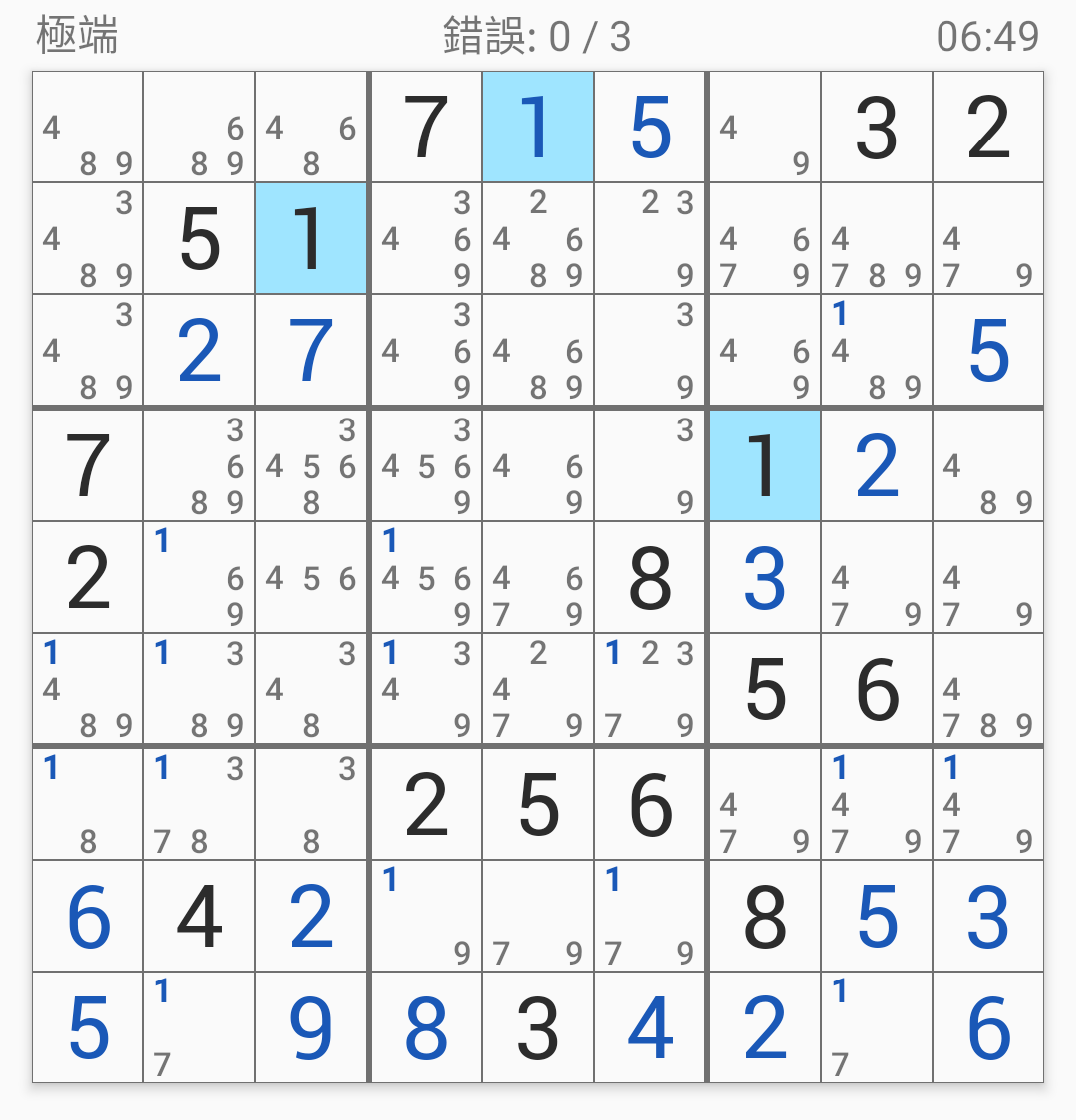
接下來注目數(shù)字1,
第三宮只有一個位置能填1了,
所以把1填一填:
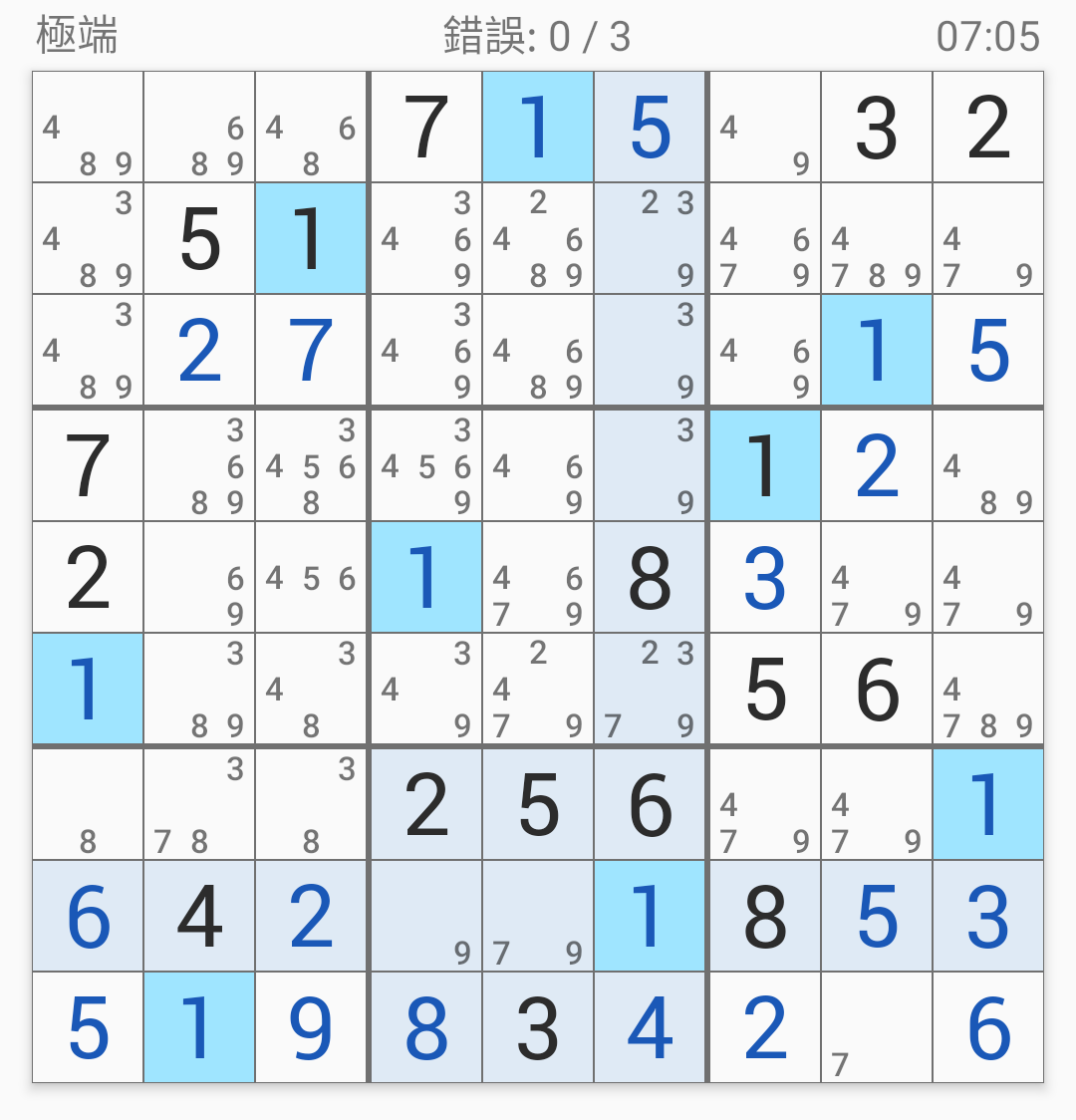
接著再把一些已知也填一填:
從第八宮的9開始:
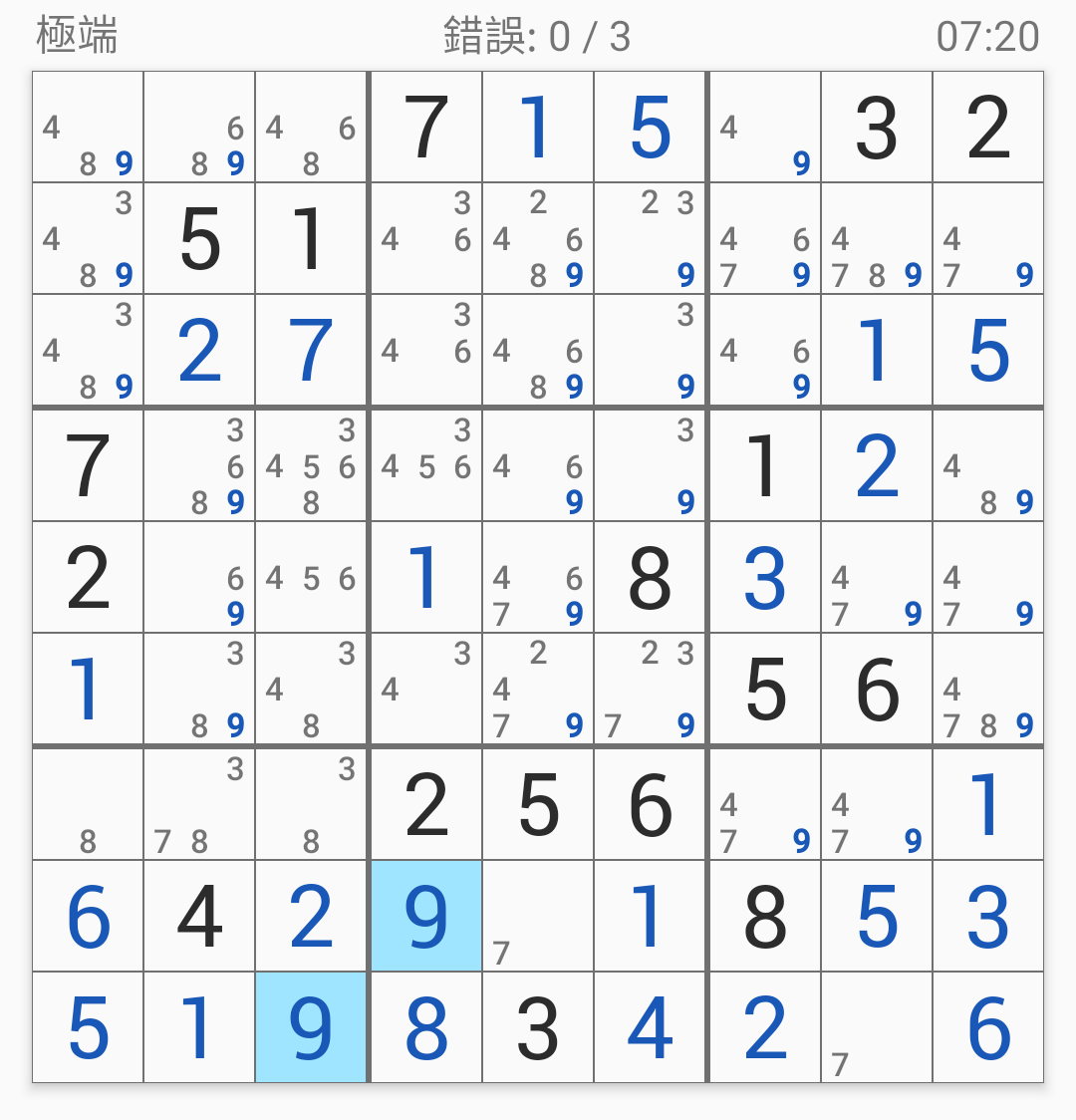
接著第八宮的7:
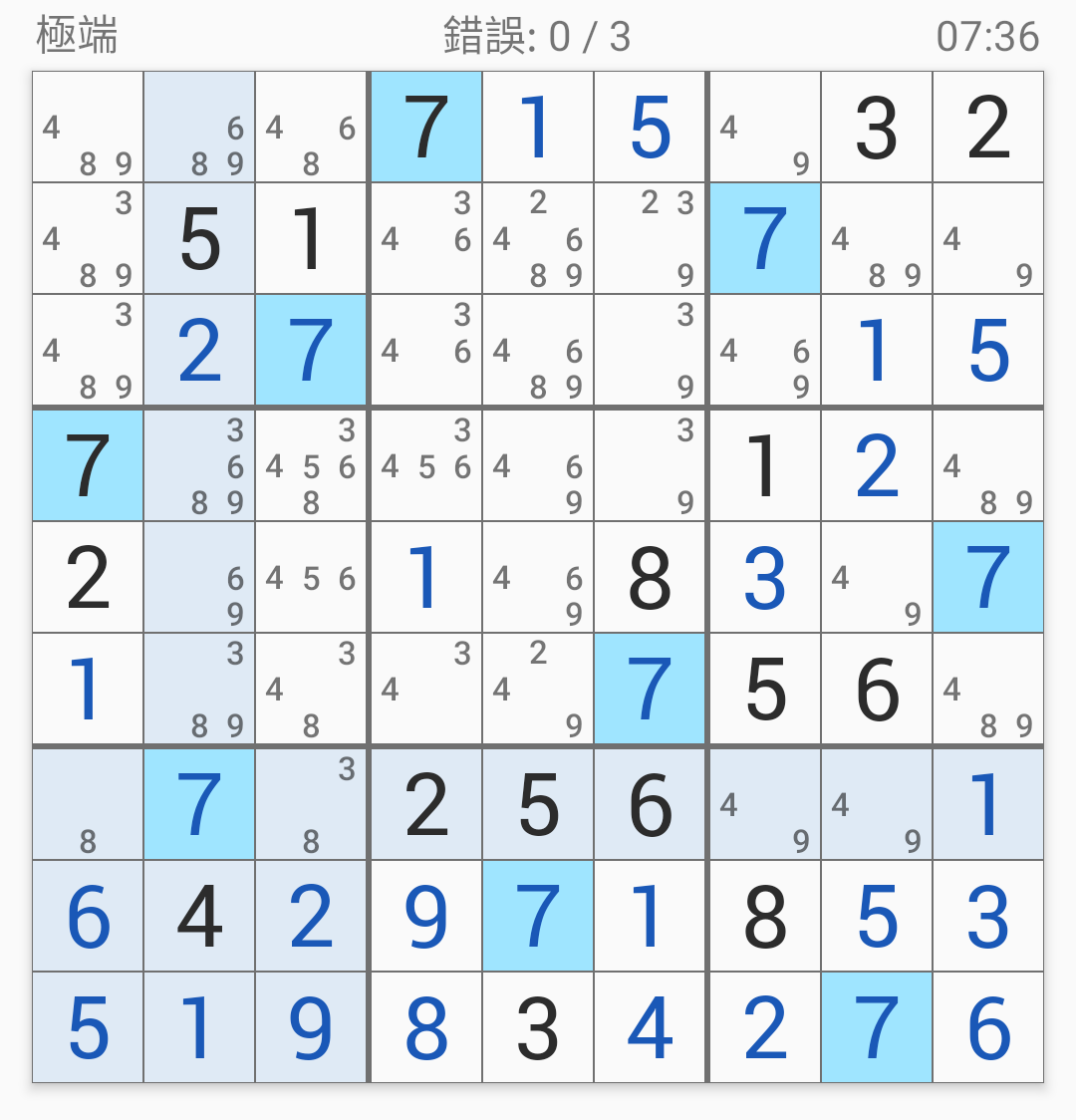
接著第七宮的8:
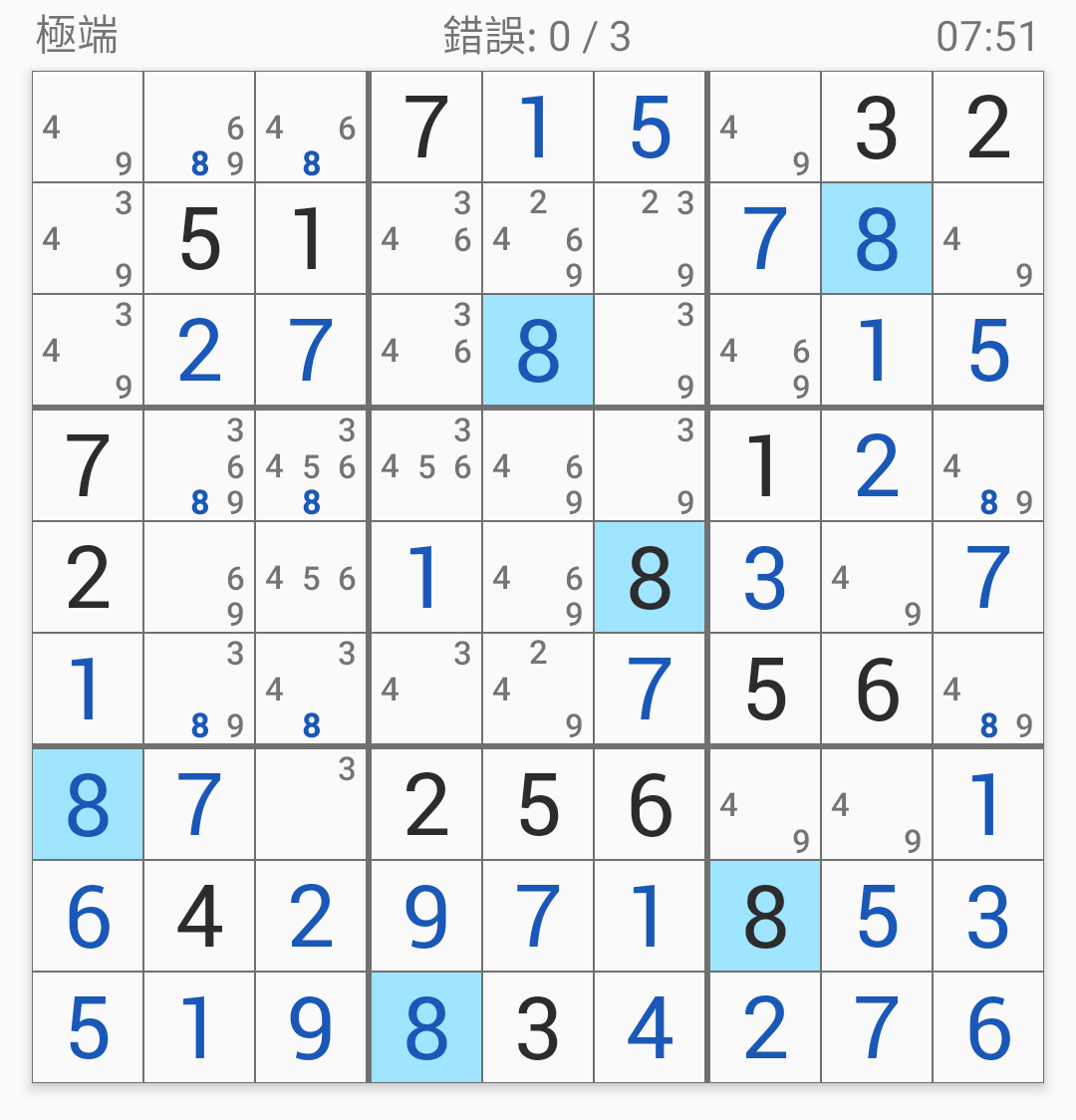
第七宮的3: 

第三宮的6: 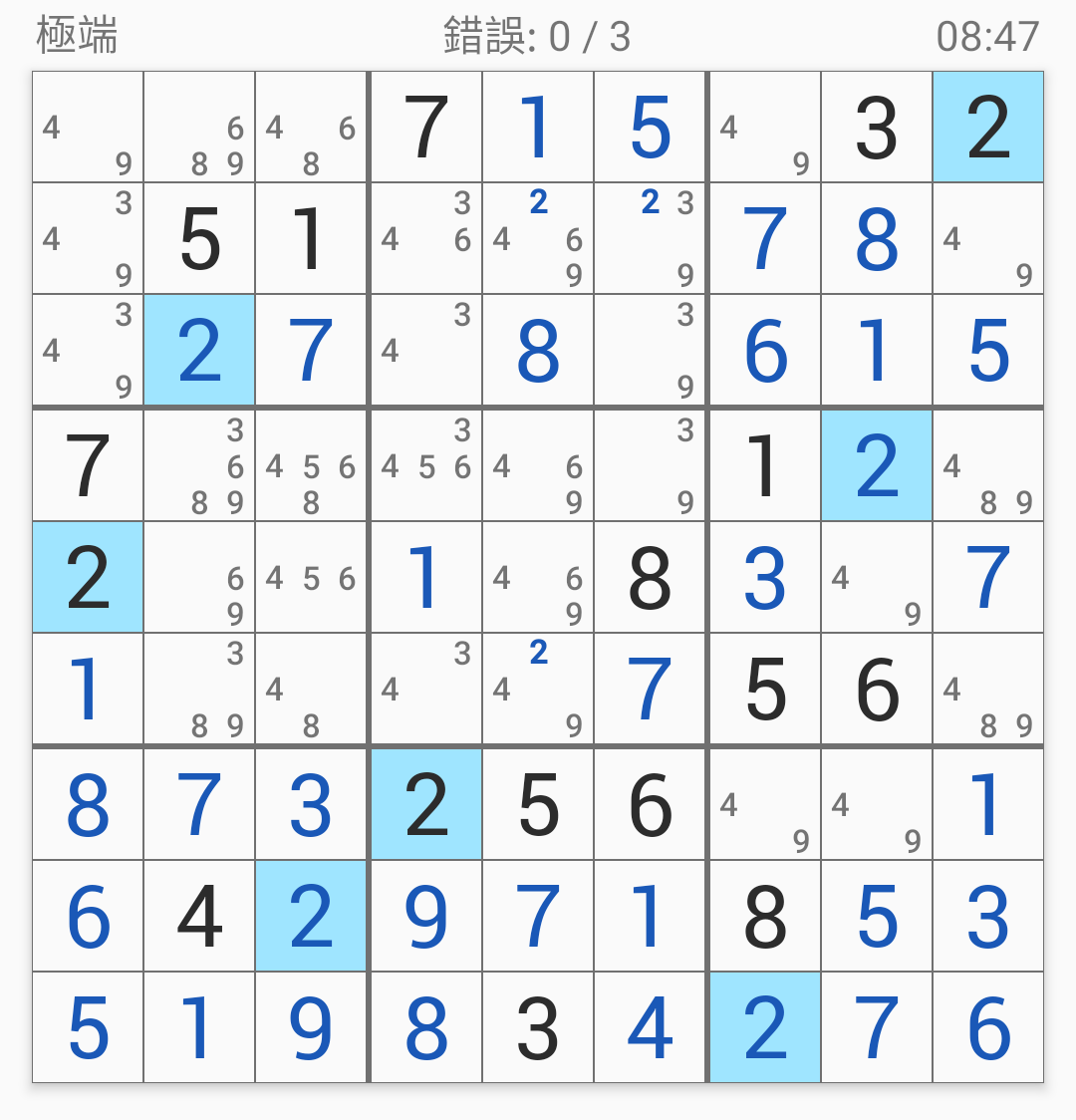

第五宮的2: 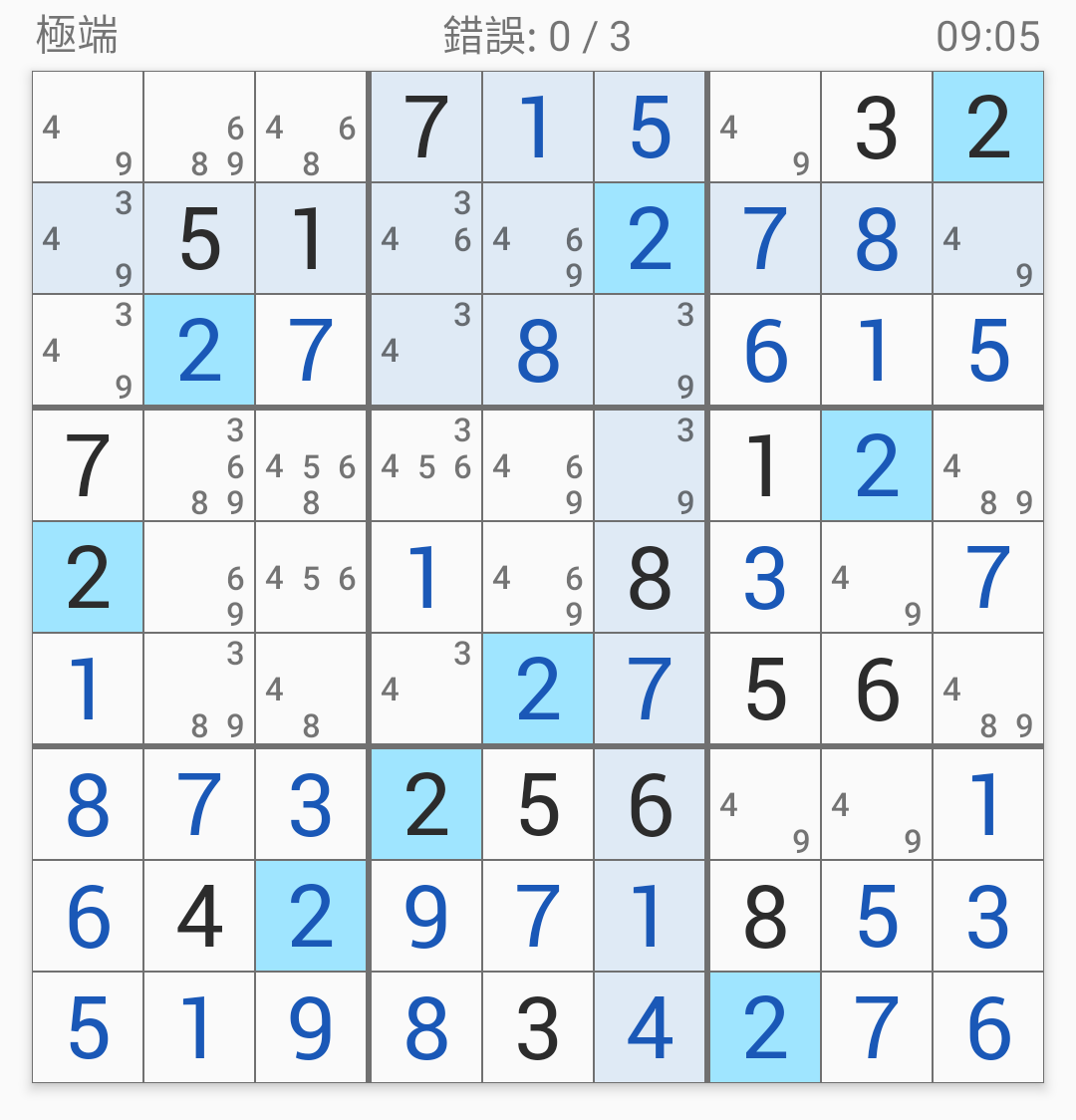

到這裡為止暫時就沒有唯一確定的格子了,
但是注意看第四列:
第四列的第三格跟第六格都是34,
這表示34必須分別在這兩格。
不管34在哪,
反正第二格都不可以是34,
因此可以消去候選數(shù)34:
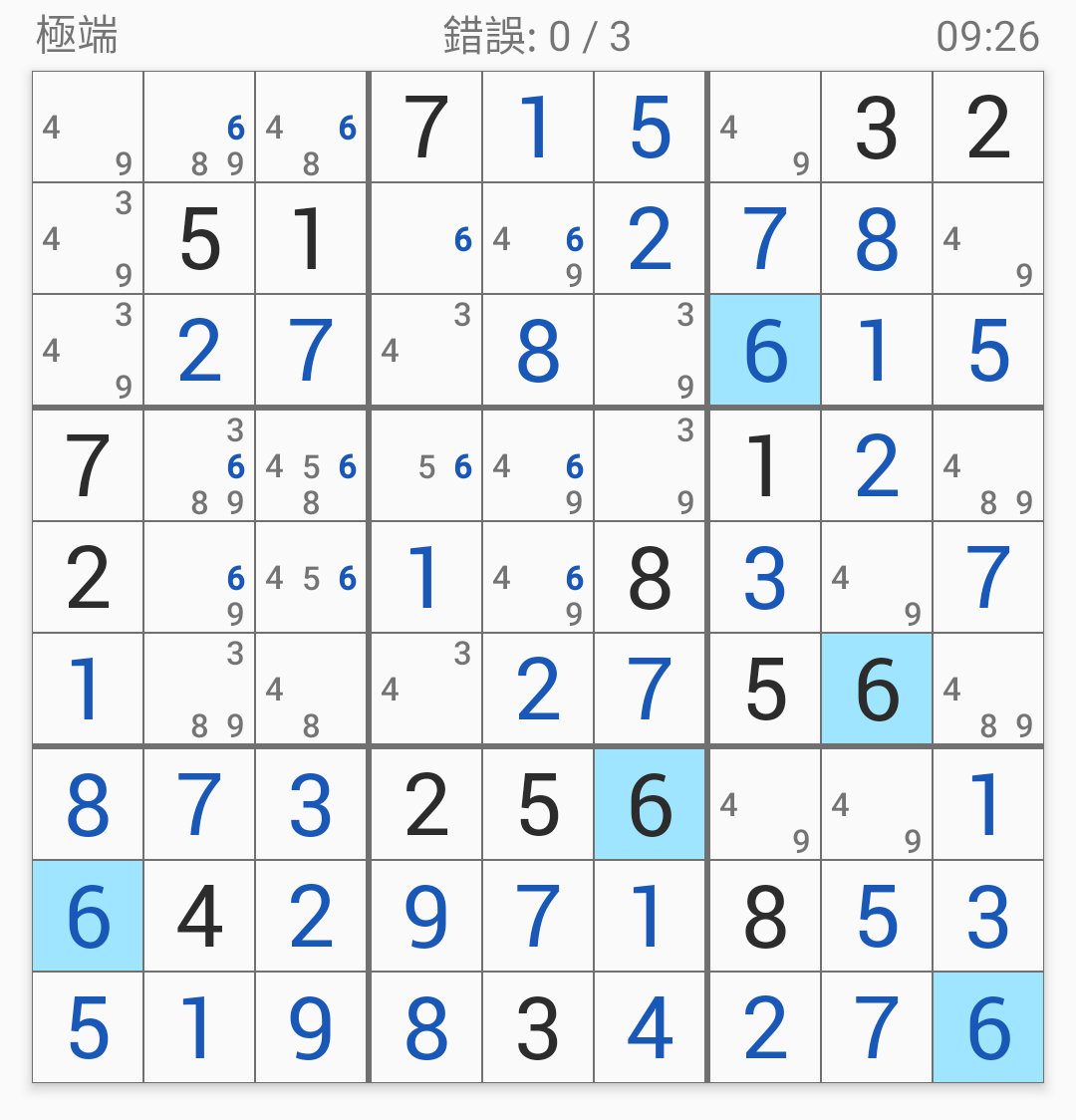
那就是填6囉!
順便把3也填一下:
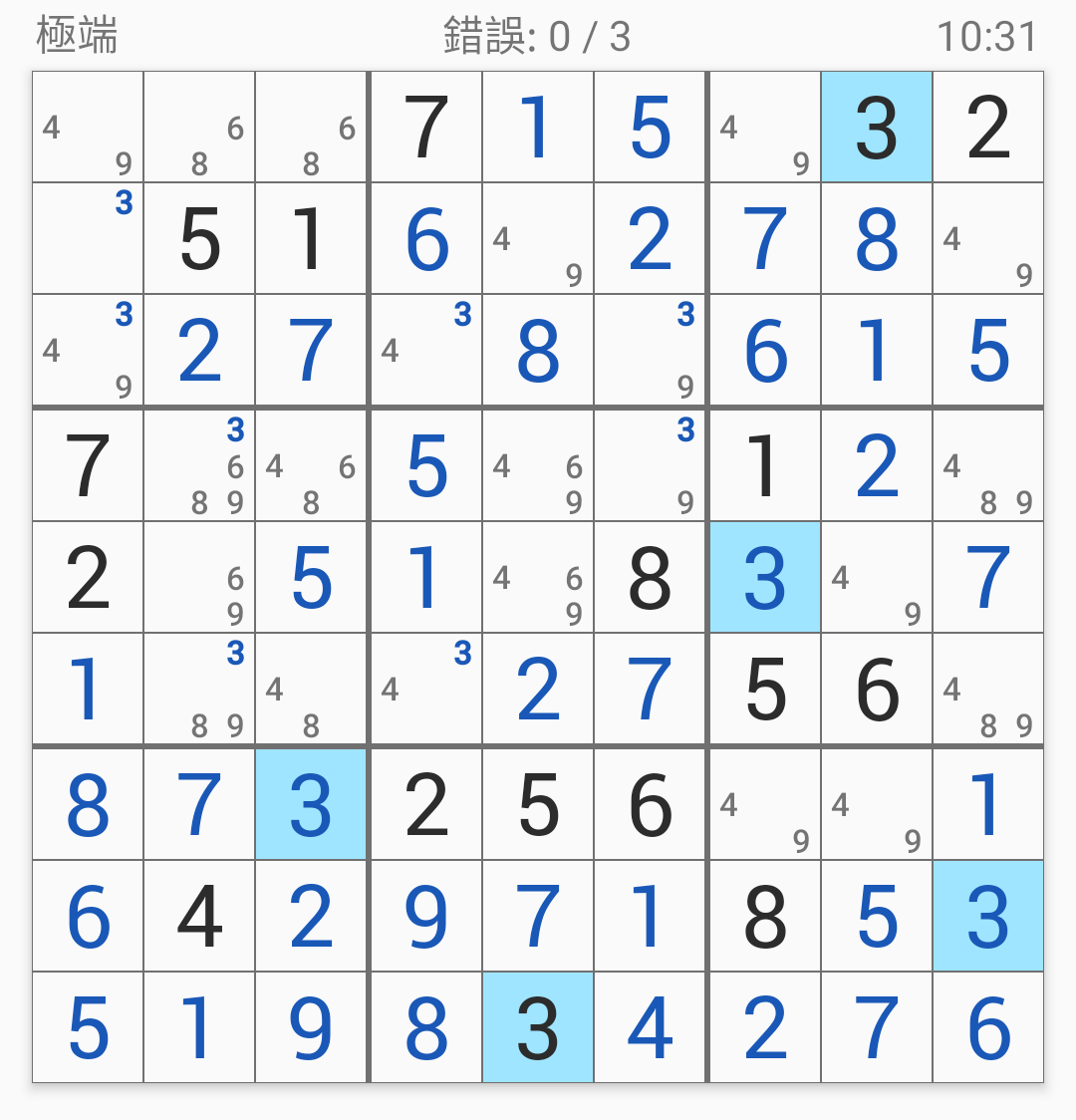
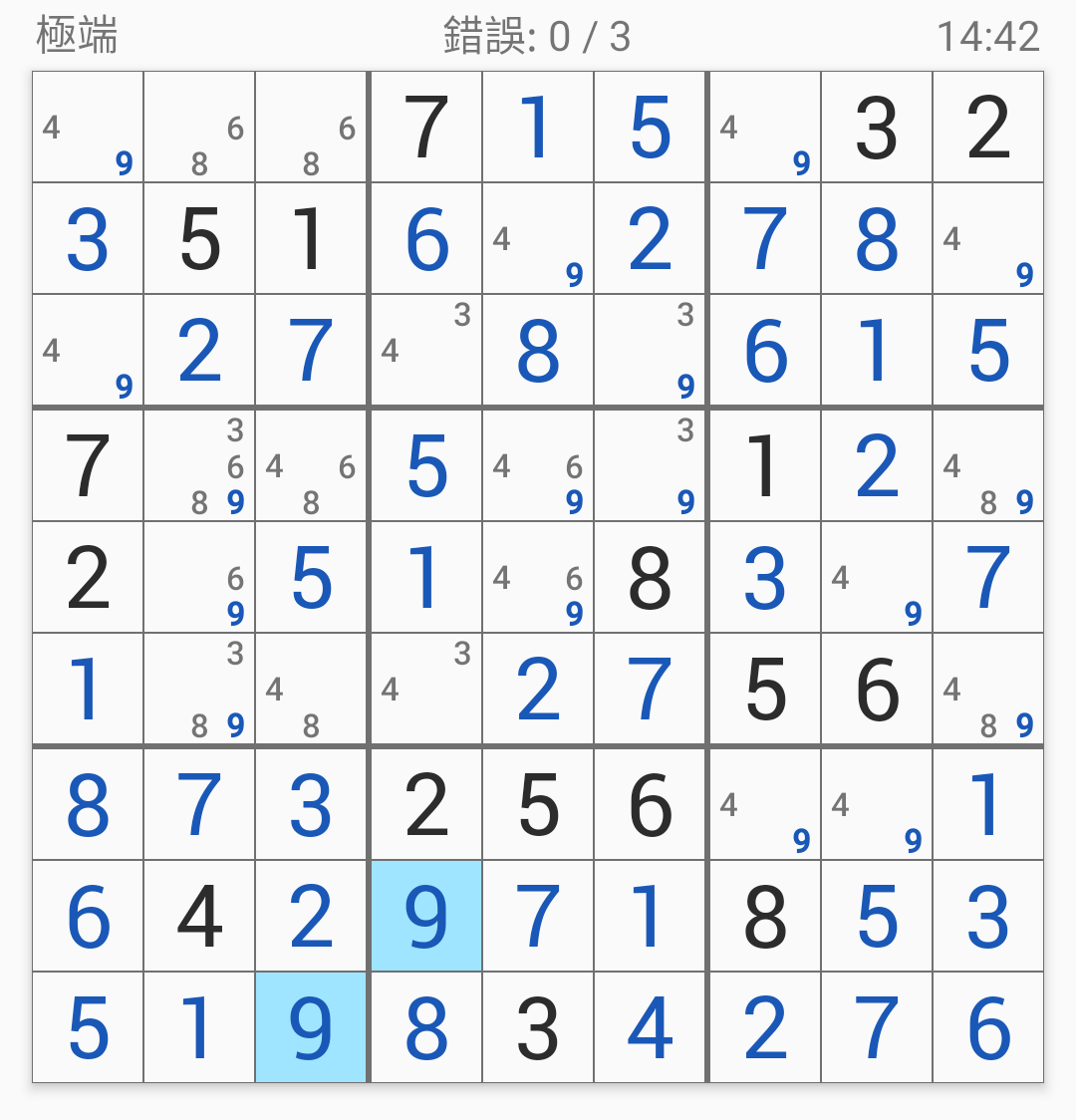
到了這一步就是一個大難關(guān)了。
正常的數(shù)獨玩家應(yīng)該都能順利解到這裡,
但接下來的步驟就必須使用到高階一點的技巧。
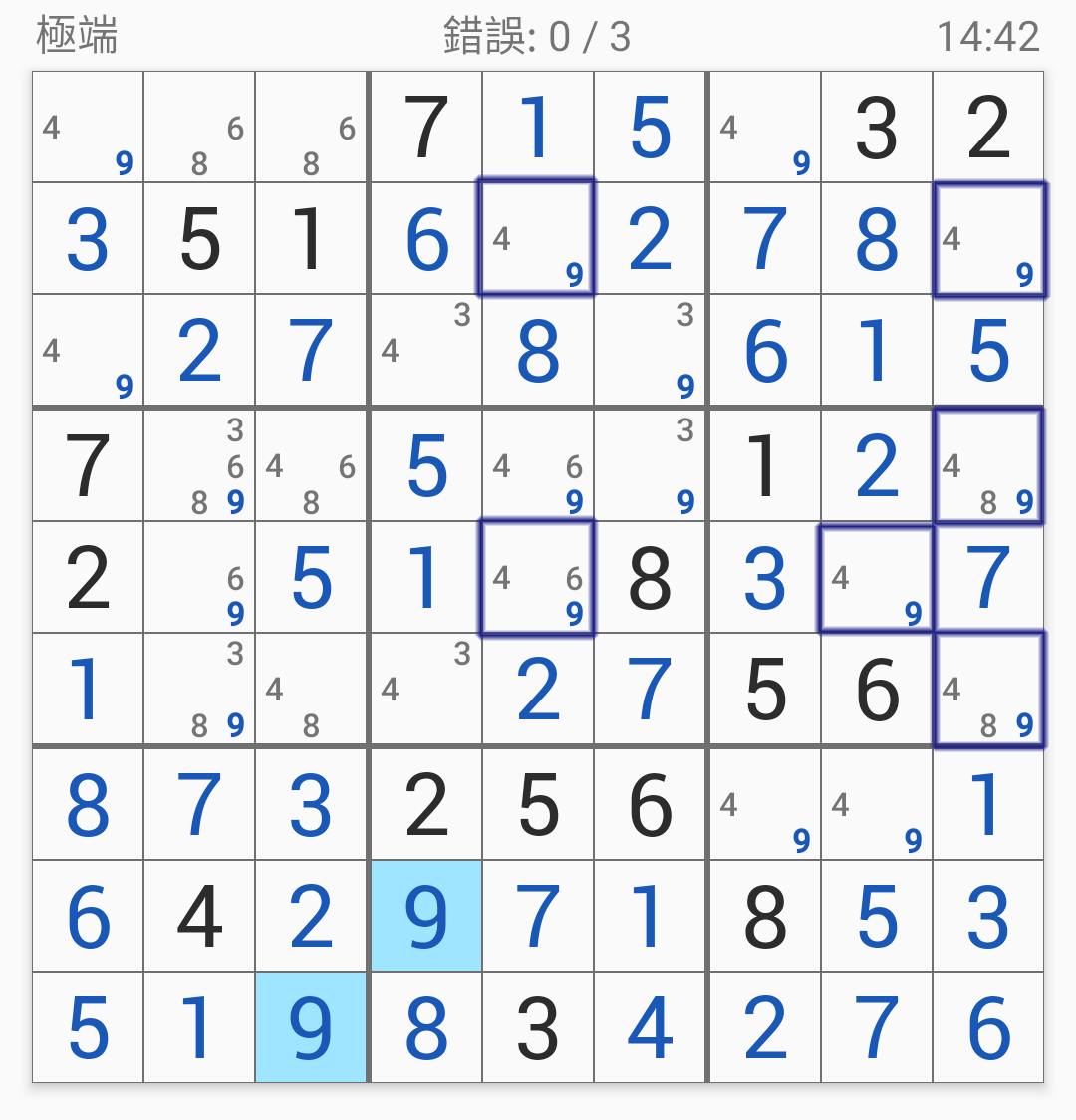
看到這種結(jié)構(gòu),
就表示可以利用「唯一性」來推出答案。
原理是這樣的,
如果有四個格子剛好組成一個矩形的四個角落,
而且候選數(shù)都是AB,
那麼這個數(shù)獨就必然有重解。
很值觀的吧?
因為你是:
AB
BA
跟
BA
AB
兩組都是合理的嘛!
所以如果這個矩形的其中一個頂點有候選數(shù)C,
那麼那個頂點的數(shù)值就必然是C才能避免發(fā)生重解的情況。
以這題的場合,
AB分別是49而C是左下角那格的6,
因此左下角那格必然填6。
到這裡,
也許你會問:
明明右下角就不是只圈一個格子而是三個格子,
為什麼可以適用這個法則?
理由很簡單,
因為他們在同一個宮裡。
因為在同一個宮就會互相影響。
以這個例題來說,
假設(shè)左上是A,
那右上就必須是B對吧?
於是右下就必須是A。
可是右下那格明明就是7而不是A?。?/div>
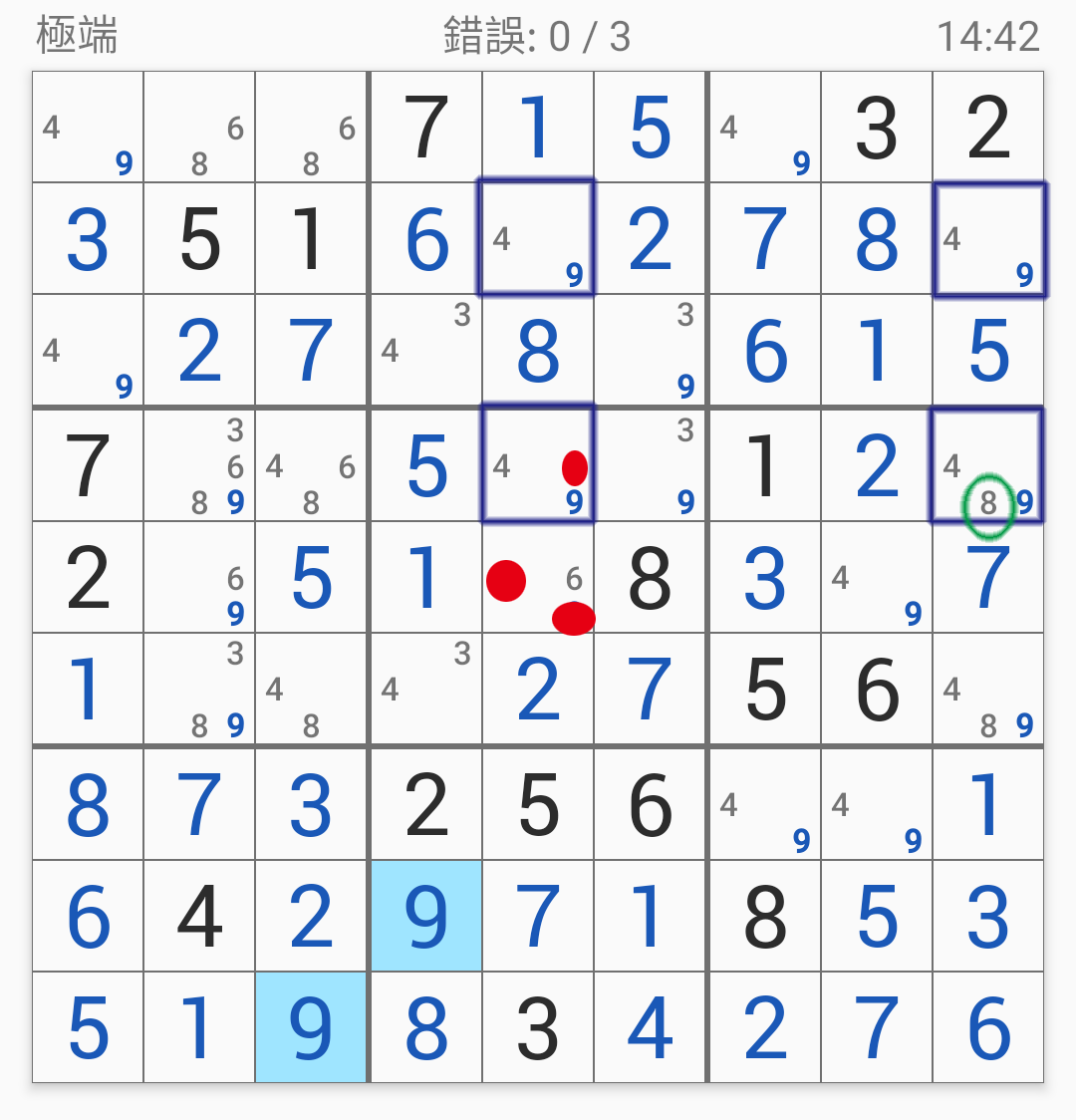


不管嘛!
因為在同一個宮裡,
右上已經(jīng)是B了,
所以跟7那格同列的格子都不能是B。
那麼B就必須出現(xiàn)在旁邊那個格子了對吧?
不然沒地方去啦!
可是它旁邊那格是不是候選數(shù)也只有AB兩個而已?
所以這格是B,
等校於7那格是A,
它都是能對左下產(chǎn)生影響的格子。
我們這裡只定義AB=49,
但A是4還是9都無所謂,
我們只需要確定左下不可以是A或B而必須是C即可。
換句話說,
我們可以肯定左下一定是C。
其實另一個看法:
左上如果是A,
那右下左邊那格必然是B,
反之亦然;
而左下同時受到左上個右下左邊那格影響,
因此必然不是A或B,
如此也能導(dǎo)出左下是C的結(jié)論。
知道左下是C,
也就是正中央是6以後,
這題就等於解開了。
上述的推理過程看起來是用了「猜猜看」的方式,
但實際上你也會發(fā)現(xiàn),
這種候選數(shù)出現(xiàn)的方式必然只有這麼一種結(jié)果,
否則要嘛出現(xiàn)重解要嘛無解,
因此做熟悉了的話看到了就可以立刻填答了,
屢試不爽。

正中央填6以後,
同樣的手法再來一次,
這次換右下有多餘的候選數(shù)C,
因此右下一定是C,
也就是8。
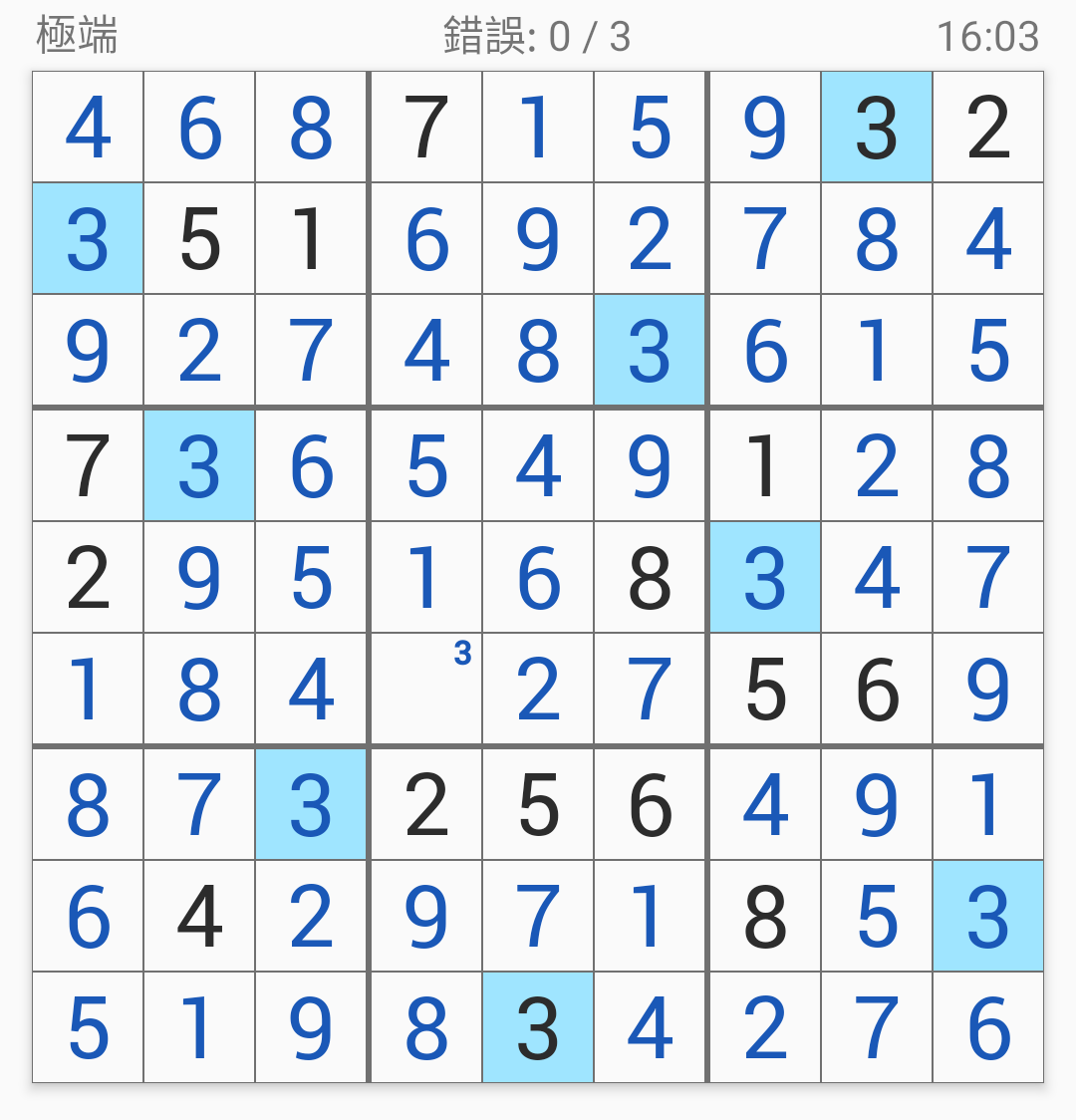
解決這個難關(guān)以後,
剩下的就是垃圾時間了。
因為沒幾個空格了,
基本上就是一路暢通到底啦!

於是這則數(shù)獨就這樣解開了。
這次選擇了高難度的唯一解數(shù)獨題來做範例,
因為沒有重解所以不會發(fā)生怎麼猜都對的情況,
解起來就相對比較有成就感,
可不是嗎?


封面圖片:《歡樂青澀甜蜜戀愛》臺灣專屬特典卡:Jia-yu(家瑜,最中二病的那隻)