題目連結:
題目意譯:
你被給定一個索引值從 0 開始數的二維整數陣列 grid,其大小為 m × n。每一個格子會有以下兩種值之一:
0,代表著一個空格子、
1,代表著一個可以被移除的障礙物。
你可以從一個空格子往上下左右移動到另一個空格子。
回傳你從左上角 (0, 0) 移動到右下角 (m - 1, n - 1) 最少所需移除的障礙物數量。
限制:
m == grid.length
n == grid[i].length
1 ≦ m, n ≦ 10 ^ 5
2 ≦ m × n ≦ 10 ^ 5
grid[i][j] 只會是 0 或是 1。
grid[0][0] == grid[m - 1][n - 1] == 0
範例測資:
範例 1:
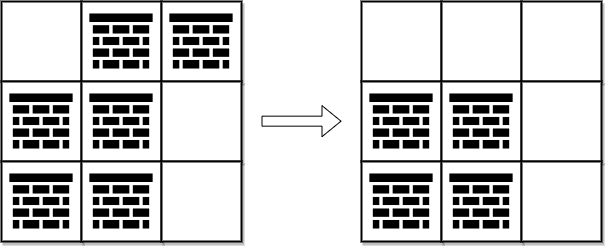
輸入: grid = [[0,1,1],[1,1,0],[1,1,0]]
輸出: 2
解釋: 我們可以移除位於 (0, 1) 和 (0, 2) 的障礙物來得到從 (0, 0) 走到 (2, 2) 的一條路徑。
可以證明我們需要移除至少 2 個障礙物,所以我們回傳 2。
注意到可能存在著其他移除 2 個障礙物來製造路徑的方式。
範例 2:
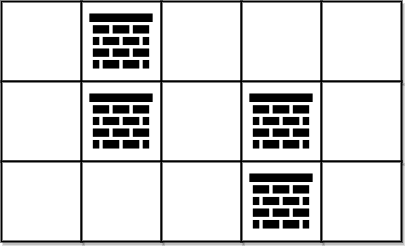
輸入: grid = [[0,1,0,0,0],[0,1,0,1,0],[0,0,0,1,0]]
輸出: 0
解釋: 我們可以不移除任何障礙物從 (0, 0) 走到 (2, 4),所以我們回傳 0。
解題思維:
可以看到,最簡單直接的方式是先看從 (0, 0) 在不移除任何障礙物下可以走到哪些格子(注意到起點和終點在本題限制條件中,一定會是空格子)。然後對這些格子繼續走到那些需要恰好移除一個障礙物才能走到的地方。以此類推直到走到終點的那一個格子為止。
很明顯地,雖然這個點子可行但實作亂寫的話時間複雜度會炸開。
而如果我們把從起點走到每一個格子的最少所需移除的障礙物數視為「距離值」,則本題即是一題相當普通的單一起點最短路徑(Single-Source Shortest Path)之題型。如
這題。也就是說,如果有一個格子是障礙物,則其上下左右四格走到此格的「成本」為 1;反之為 0。因此經典的演算法如「戴克斯特拉演算法」(Dijkstra's Algorithm)即可達成要求。
但今天不是要講解 Dijkstra 演算法(儘管下面還是會說明)。今天要介紹的是一個特別的演算法——「0-1 BFS」,其可以視為是 Dijkstra 演算法的變體。但僅僅只適用於邊的成本為 0 或是 1(故得其名)的圖,且一樣只能求單一起點最短路徑。至於 BFS 就只是指這個演算法中有一個廣度優先搜尋(Breadth First Search)而已,連 Dijkstra 其實也有。
Dijkstra 的精神是「已知某些點到起點的最短距離」,則「從那些點走到的其他點也『可以得到』從起點的最短距離」(寫作『可以得到』是因為可能有多個點可以走到同一個點,取其中最小者才是真的最短距離)。
因此 Dijkstra 通常會有一個優先佇列(Priority Queue)來儲存當前擴張到的點哪一個是距離最小者(一開始,只有起點本身會在佇列中)。
所以如果用一個鄰接表(Adjacency List)來存邊的資訊(本題連存都不用就是了,因為固定只會是當前格子的上下左右)且實作用的優先佇列是一個普通的堆積(Heap)的話,則時間複雜度會是 O(E + V × log(E)),其中 E 是邊數、 V 是點數。但因為本題每一個格子最多四個邊(一樣,是上下左右),因此時間複雜度實際上是 O(V × log(V))。
但是如果我們回到一開始提及的方式——最初會是走到那些移除 0 個障礙物的格子、再來是那些移除 1 個障礙物的格子、……以此類推。
假設現在優先佇列丟出來了一個最小距離值 X,而由於圖上的邊成本只有 0 或是 1,因此當前這個格子擴張到其他格子後只會得到 X 或是 X + 1 的距離值而已。而只要優先佇列中還有最小距離值為 X 的格子存在,它們必定會先於 X + 1 或更大的值出來。
也因此直到 X 這個距離值從優先佇列完全消失前,我們是不會去擴張到那些 X + 1 的格子的(沒錯,這個概念單純但重要到我需要換句話說好幾次 XD)。正因如此,實際上這個優先佇列一次只會有兩種數值。
而既然如此,為何還需要優先佇列來維護當前最小距離值?不是只要用一個雙端佇列(Deque)來存不就好了嗎?
也就是說只要現在擴張到的格子會得到與現在相同的距離值(如上例的 X),則將該格子丟到雙端佇列的「左側」;然後如果擴張到的格子距離值是現在的 + 1(如上例的 X + 1),則將該格子丟到雙端佇列的「右側」。這樣一來不管 X 是什麼值,該佇列永遠都會保持著 [X, X, ……, X, X + 1, X + 1, ……, X + 1] 之形式。完全不需要額外的排序或是其他的維護。
也因此對於成本只會是 0 或 1 的圖來說,單一起點最短路徑按照上面的想法實際上可以做到 O(E + V)。而對於本題來說即是 O(V) = O(mn),即線性時間。
而這就是「0-1 BFS」。
此次分享到此為止,如有任何更加簡潔的想法或是有說明不清楚之地方,也煩請各位大大撥冗討論。