題目連結:
題目意譯:
在一個大小為 2 × 3 的版面上有著編號為 1 到 5 的五個磁磚,以及一個空格子,其以 0 表示。一「步」定義為選定 0 以及四方向相鄰的數字並將兩數的位置交換。
版面是「解開」的狀態若且唯若版面是 [[1,2,3],[4,5,0]] 之狀態。
給定謎題的版面 board,回傳將 board 變成「解開」的狀態最少所需步數。如果不可能解開,則回傳 -1。
限制:
board.length == 2
board[i].length == 3
0 ≦ board[i][j] ≦ 5
board[i][j] 之值彼此相異。
範例測資:
範例 1:
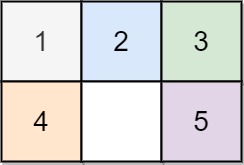
輸入: board = [[1,2,3],[4,0,5]]
輸出: 1
解釋: 用一步交換 0 和 5。
範例 2:
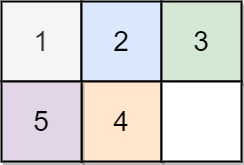
輸入: board = [[1,2,3],[5,4,0]]
輸出: -1
解釋: 不可能解開這個版面。
範例 3:
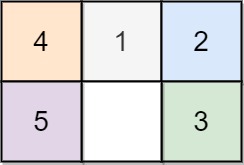
輸入: board = [[4,1,2],[5,0,3]]
輸出: 5
解釋: 5 是最少所需的步數。
其中一種方式為:
一開始: [[4,1,2],[5,0,3]]
第 1 步後:[[4,1,2],[0,5,3]]
第 2 步後:[[0,1,2],[4,5,3]]
第 3 步後:[[1,0,2],[4,5,3]]
第 4 步後:[[1,2,0],[4,5,3]]
第 5 步後:[[1,2,3],[4,5,0]]
解題思維:
可以看到最多只會有 6! = 720 種可能的版面(包含那些不可解的)。
因此,直接從一開始的版面 board 進行廣度優先搜尋(Breadth First Search,BFS)來持續地看「下一步」可以走到哪些版面。
如果有版面重複出現則無視(跟一般的 BFS 一致),而要檢查有沒有出現過可以直接用一個 6 × 6 × 6 × 6 × 6 × 6 的六維布林陣列(一個維度代表一個格子,什麼數字出現在什麼格子,該格的「索引值」即為該數;不過由於「第六格」會被其他五格決定出來,因此實際上可以降低成五維陣列)來檢查。
如果過程中有遇到「解開」的狀態,則此時 BFS 擴張的步數即為所求;如果掃完所有從起始版面可以走到的版面都沒有遇到,則代表不可能解開,此時回傳 -1。
可以看到每一個版面會檢查 0 這個數字往「上下左右」方向移動的四種可能性並且每一次「當下」的版面要重新生成。因此時間複雜度為 O(4 × 6 × 6!)。
此次分享到此為止,如有任何更加簡潔的想法或是有說明不清楚之地方,也煩請各位大大撥冗討論。