緣起是小學奧數(奧林匹克數學競賽)題目。題目內容是很典型的二元一次方程組題型。由於是「小學奧數」,因此被限定只能用小學生理解範圍內的解題方式。簡單說嘛,就是畫數線,
而此時亞夜說了:「不就是加減消去法?」隨後又說:「二元一次方程組說白了也就代入消去法跟加減消去法兩種而已,什麼特殊解法最終還是繞不開加減消去法。」於是就開始有人說什麼「高斯消去法」啦「行列式法」啦等等,欸,不是國小奧數嗎?連高中的東西都出現了……
不過做人要負責任,既然提了就要給人家解釋清楚。為什麼亞夜認為,加減消去法就夠了。
在此之前還是先講一下什麼叫「方程組」。方程組又稱「聯立方程式」,簡單說就是有好幾組方程式,將他們並列在一起後且必須「同時成立」,因此稱為「聯立」。因此當中最基本的就是二元一次,也就是由兩條具有兩個未知數的線性方程式所組成的方程組。
最基本的方程式是一元一次方程式。而國小高年級裡面提到的「怎樣解題」裡面就有提到所謂「未知數」的觀念。而其實這個「未知數」說白了就是所謂的「方程式」的基本觀念,所以國小奧數題最喜歡的題目就是二元一次的方程式題,因為一元一次方程式稍微拓展一下就行了,雖然超綱了但卻也是用現有知識就能解的題目。
而二元一次方程組通常由兩個方程式組成。因此我們首先要做的就是「消元」,將其中一個未知數表現為另一個未知數的形式。
首先就是要使用一組方程式,藉由移項來將一個未知數表達成另一個未知數的形式,接著我們用這個條件帶入另一組方程式裡,就能得到一個一元一次方程式,進而求出答案。舉例來說:
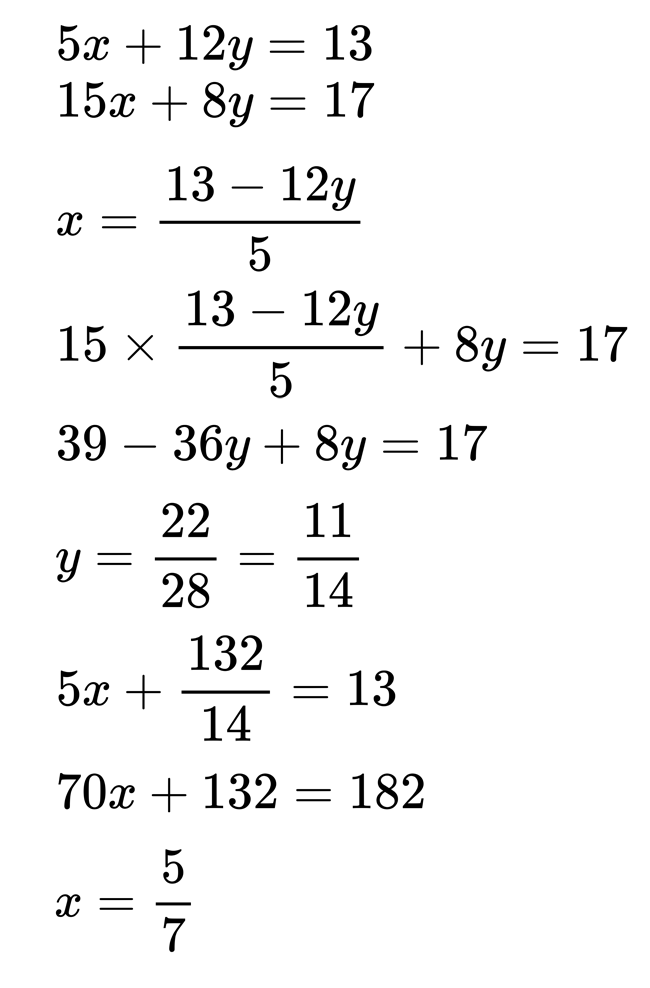
以上這種解法稱為:代入消去法。
「代入消去法」的好處是夠直觀,幾乎不需要任何特殊技巧,只要懂得方程式的移項規則,也就是所謂的「等量運算」原則,任何有解的線性方程組都一定能解的出來。
不過缺點嘛……就是計算量可能會很大。因為最終你為了消元就要除掉係數,因此只要係數不是 1 就會跑出分數進而造成困擾。當然,如果係數是 1 的話那問題倒是不大就是了。
原則上學會「代入消去法」後就能解決所有有唯一解的線性方程組。不過為了節約計算量,通常這時課綱會教另一種解法:「加減消去法」。
加減消去法的操作原則是,把方程組各自乘以一個係數,讓其中兩個方程式的某一個未知數的係數相同,這樣就能利用減法的方式消元,進而求出答案。舉例來說:

可以發現,加減消去法比起代入消去法而言減輕了非常多的計算量,因此也是解方程組時最主力的計算方式。
簡單來說,解線性方程組,那就只有「代入消去法」與「加減消去法」兩種解法。而通常會使用的是後者,因此學到這裡,線性方程組的求解基本上就完事了。
【克拉瑪公式】
這時可能就有人要罵亞夜了:明明還有所謂「公式解」。只有兩種解法不會說的太武斷嗎?
並不會。
在講克拉瑪公式之前,要先講行列式。唉,這下就又 match 標題了,亞夜實在很不想教行列式,尤其是用來解方程組。
講行列式之前就要先講矩陣,先借用維基百科的圖:
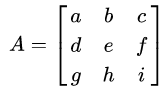
能夠寫成這種形式的就叫做矩陣。矩陣只要是方形的就型,而不一定要正方形。然後這東西是一個純量,所以可以做四則運算。當中,乘法的做法是:「被乘矩陣的橫行,乘以乘矩陣的縱列,如此反覆直到每一個元素都算出來後再加總。」
看起來很複雜?我們直接做例題比較簡單:
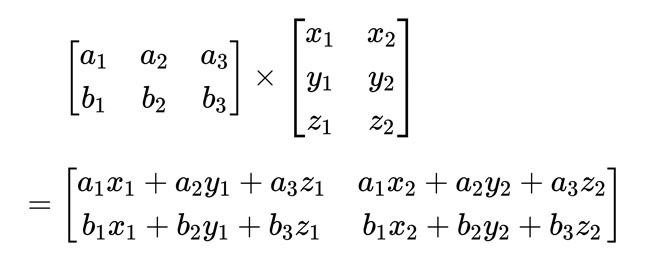
很複雜嗎?其實順序是這樣的:
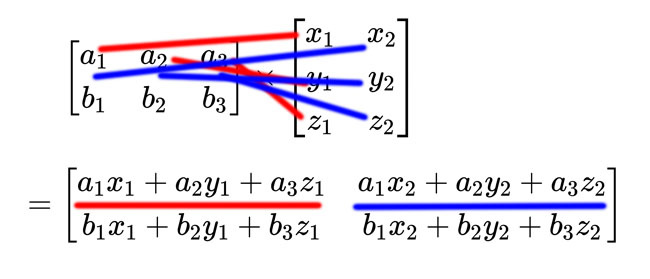
簡單說就是,左邊的橫行乘以右邊的直行,對應元素個別乘,然後加起來。
然後他是左邊第幾行乘以右邊第幾列,結果就是第幾行第幾列。
換句話說,結果的矩陣的行數會跟左邊相同,列數會跟右邊相同。以這個例子為例,兩行乘以兩列,因此結果就是2×2的矩陣。
為什麼要了解矩陣的乘法?因為可以這樣做:
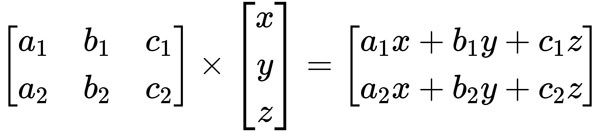
到這裡,這不就是一個方程組嗎?
繞了一大圈,就只是要把方程組寫成「矩陣」的形式。而那是為什麼?只為了要使用行列式來求解方程組。
OK,行列式出現了。那麼什麼是行列式呢?行列式簡單說就是,矩陣的值。而二階行列式的算法是,矩陣左上往右下的對角線,減去右上往左下的對角線。至於更高階的行列式,則必須透過降階的方式求解。
喔順道一題,只有「方形」的矩陣可以求行列式。所以一定有對角線。
先看二階行列式。簡單來說,定義是這樣:
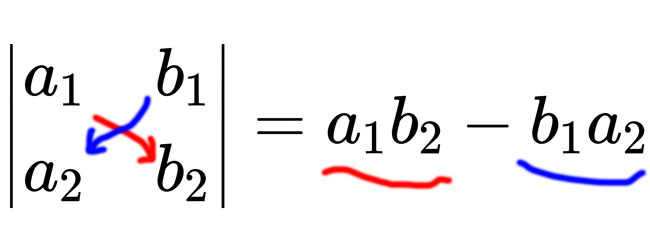
知道這可以幹嘛?可以套公式。
我們上面說了,方程組可以寫成矩陣相乘的形式:
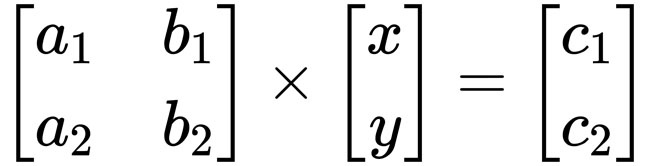
這個形式等效於
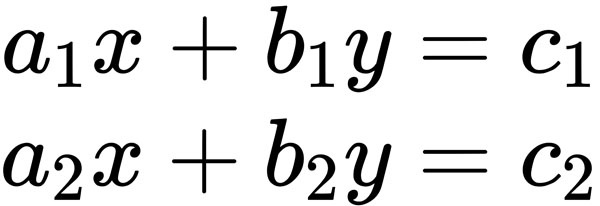
那麼寫成這個形式可以幹嘛呢?答案是變魔法。
嘛,其實不是變魔法,而是套用克拉瑪定理。
克拉瑪定理具體證明亞夜就不做了,那個因為牽涉到空間向量。一般來說二元(平面)跟三元(立體)還能想像,四元以上的根本連想像都做不到了。因此直接說結論:
對於上述形式的矩陣方程式,定義幾個關鍵值:
被乘矩陣的行列式為「Δ」。
用積矩陣取代被乘矩陣的第n列,則該矩陣的行列式為「Δn」。
然後n=Δn/Δ。
看不懂嗎?沒關係,直接列式子就懂了:
以這個方程式為例:
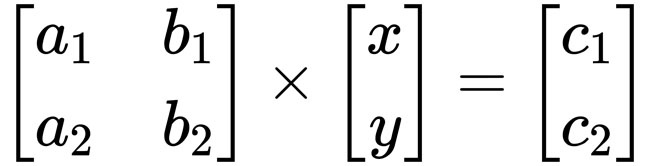
則:
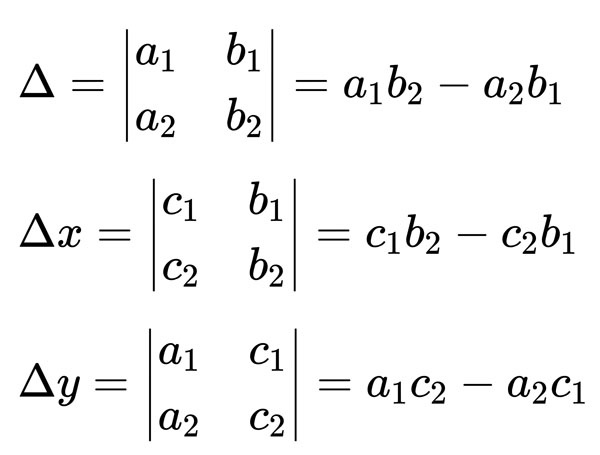
因此帶入公式:
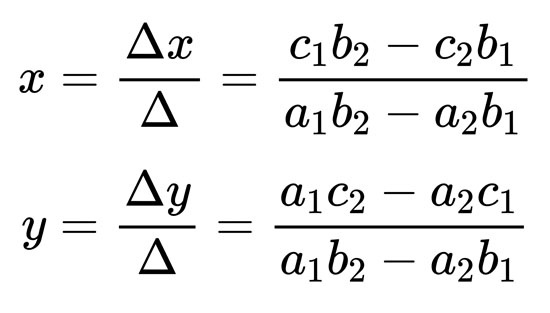
轉眼間,解就求出來了,真是太棒了有沒有……才怪,並沒有好嗎?
當然學生要背這個公式,亞夜也不會去阻止,但問題是,這個公式並不會簡化學生的計算量,因此背它完全沒有意思。
怎麼說?我們如果用加減消去法去做這道題,要怎麼做?
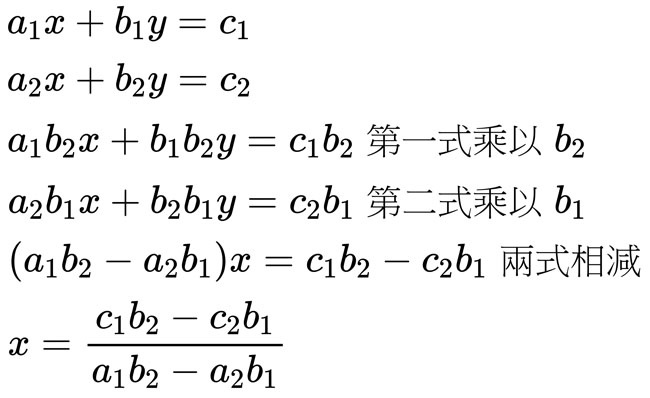
有沒有看出端倪?
乍看之下,步驟變多,好像比較複雜?其實並沒有。為了使用加減消去法消元,我們必須對兩個式子都乘以一個數字。可你有沒有注意到你真的需要「乘開」的項目是什麼?是不是跟克拉瑪公式裡面你需要親自「乘開」的東西完全一樣?所以結果來說,克拉瑪公式只是加減消去法的簡潔表現形式而已,它的優點在於公式寫起來簡潔,但計算量本身其實並沒有減少。
所以克拉瑪公式是不是多元一次方程組的解題方式?的確是。
那麼多元一次方程組只有「代入消去法」與「加減消去法」兩種解法是錯的。當然不能這麼說。克拉瑪公式最終不過就是加減消去法的「代數表達式」,因此本質上仍是加減消去法。如果只是加以延伸變化就能說是「不一樣」的解法,那麼亞夜也能用加減消去法改個步驟,然後重新命名叫「亞夜消去法」,然後大家都來學習亞夜消去法來解方程組嗎?(於是從此以後,亞夜被從這個世界上消去了)
雖說不是不行,但真的沒有意義。因為這樣只會讓學生浪費一堆時間去學習「重複」的東西而已。
那為什麼課綱要教克拉瑪公式?克拉瑪公式真的有那麼尊爵不凡,值的學生花半個學期去學嗎?
當然說克拉瑪公式完全沒用也不對,只是它的用處其實沒有你想像中的大。就好比九九乘法,你用建構式數學的「連加法」一樣可以求解,但是背九九乘法則可以大幅縮短計算時間,這是有意義的;可是印度學生的「九九九九乘法」,把九九乘法從一位數拓展到二位數,需要背誦的項目從 81 項爆增到 9801 項,難度多了 121 倍,然後你得到了多少效益?如果不考慮效益,那為什麼不背「九九九九九九乘法」?為什麼不背「九九九九九九九九乘法」?瘋了?不是一樣意思嗎?
同樣的道理,加減消去法比起代入消去法有計算量上的絕對優勢,因此它值得學習;但克拉瑪公式之於加減消去法,就相當於九九九九乘法表之於九九乘法表,它的效益並沒有那麼大,因此亞夜認為這不過就是徒增學生壓力罷了。這種就適合放在選修數學,讓「真的很閒」的學生自主學習,而不是放到主要課綱裡逼著大家都要學。
這時有人會說了:克拉瑪公式的一大優勢就是能快速判斷方程組是否「有解」。
具體怎麼說?上面不是要把 Δ 放到分母嗎?那如果分母為 0 就出事了嘛!所以從克拉瑪公式就能很簡單的判斷:只要 Δ=0,那麼方程組不是無解就是無窮多解。
但是我們回到方程組的幾何意義來思考這件事,你會發現這個判斷式本身計算量仍然不會減少。一個多元一次方程式的幾何意義是什麼?
方程式的解的集合就是方程式的圖形,因此一元代表一個點、二元代表一條直線、三元代表一個平面、四元代表一個空間……以此類推。
當考慮到二元的部分,方程組解的意義是同時滿足所有方方程式的點的集合。既然單一一個二元一次方程式的解為直線,那麼二元一次方程組的解就是兩條直線的「交點」。
通常情況下兩條直線只會有一個交點。因此,通常情況下只會有一組解。不過,如果兩條直線「重合」,也就是說兩條方程式完全一模一樣時,那麼自然就會有無窮多解了。反之,如果兩條直線「平行」,那麼理所當然的就不會有交點,也就是無解。
那麼問題就在這了。加減消去法如何知道是否是「唯一解」?其實很簡單,因為你要做加減消去法,必然得先幫兩個式子各乘上一個係數(依照情況不同,當然可以是 1),目的是為了讓其中一個未知數的係數相等以方便進行「消元」的動作。而此時,如果兩個未知數會「同時」消掉,那麼這組方程組就會變成要嘛無解、要嘛無窮多解的情況。
舉個例子:
9x+12y=10
6x+8y=7
為了消去 y,把第一式乘上 2、第二式乘上 3,得到新的方程組為:
18x+24y=20
18x+24y=21
這時你發現 x 會同時消掉,那麼就滿足條件了。這個情形充要於消元時發生 0x+0y=a 的情況,其實觀察力好一點的同學早就會發現:當兩式的 x、y 的係數比相同時,那麼此方程組就不是唯一解。
為什麼係數比會相同?因為係數比決定斜率,而平行線的特徵就是「斜率相同」。重合線就更不用說了,都同條線了當然斜率也相同,因此係數比相同充要於斜率相同,而斜率相同充要於不是唯一解。
※充要=充分且必要。即代表兩者為「同一件事」。
同時,x、y 係數比相同也同時充要於 Δ=0。請看以下推導:
係數比相同怎麼表達?在數學上會這樣寫:
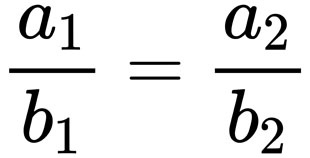
既然如此,那它將會滿足:
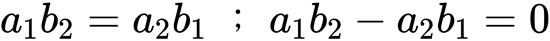
這不就跟克拉瑪公式中的 Δ=0 完全一樣嗎?
所以說,有必要背嗎?你在使用加減消去法的過程中,自然就會發現了。
克拉瑪公式中要判斷究竟是無解還是無限多解的方法是,要去判斷常數項係數的比例與未知數項的係數比例是否相同,也就是:
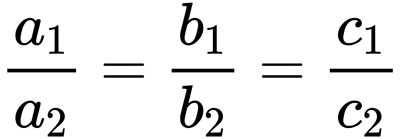
這個場合無窮多解。
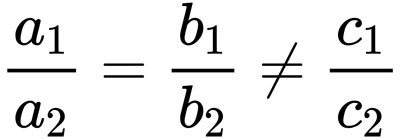
這個場合無解。
你還得去判斷比例,但在加減消去法的過程中,你消元的結果會是 0x+0y 的式子。此時常數項為 0 就是無窮多解(0x+0y=0 這不是廢話嗎?因此解有無窮多),反之無解(0x+0y 除了 0 以外還能是啥呢?)
比起還要去算常數項比例,直接減了不就一目瞭然了嗎?
而克拉瑪公式還有一個賣點:可以解二元以上的多元一次方程組。
以三元一次來說,總而言之換湯不換藥,它是這樣表達的:
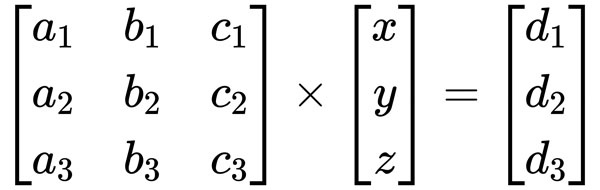
於是乎:
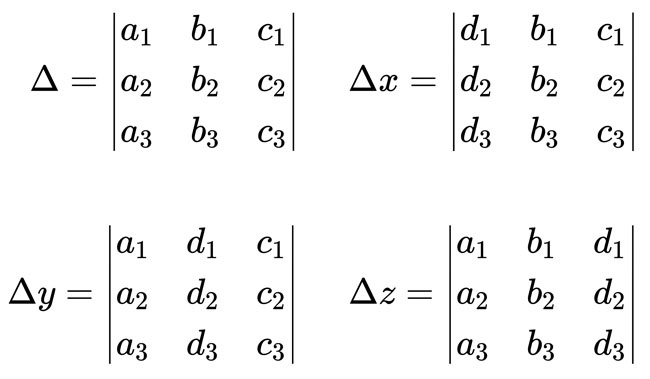
好咧,三階行列式怎麼求?有公式可以背,有點小複雜就是。總結來說就是降階。
行列式怎麼降階?
選定第一行(方便起見),然後每個元素依序乘上餘元素的行列式。
奇數項為正,偶數項為負。最後加總即可。
※餘元素:「與指定元素同行或同列的全部刪除,剩下來的部分」
文字說明不好理解?直接做一次就懂了:
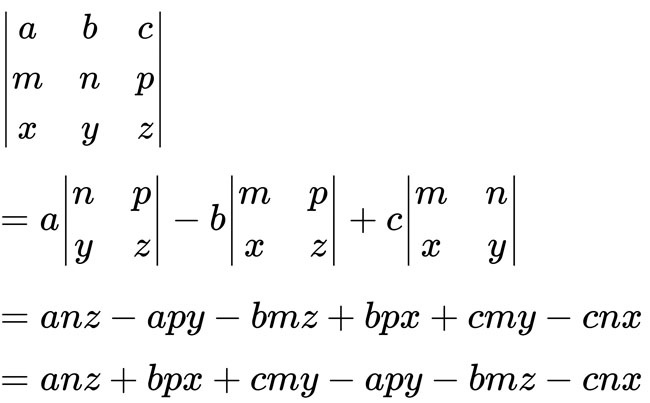
為什麼要寫成這個樣子?單純是為了公式好記,因為它其實長這樣:
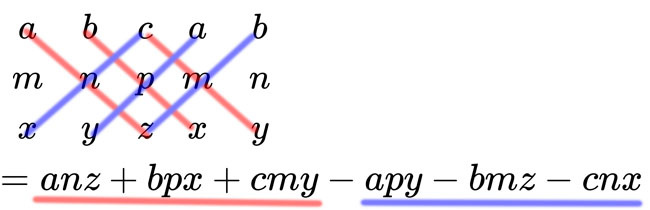
雖然還算好記,但其實計算量根本一點都不小。
好啦,所以我們試著用克拉瑪公式來解三元一次方程組。因為方法是一樣的,所以就只做 x 的部分而已:
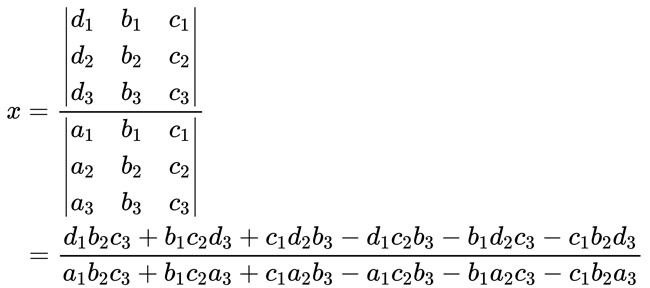
有沒有看到馬上就不想算了?有夠混亂的,重點是,三階行列式超級容易算錯。
那麼正規解法呢?高中在講三元一次方程組時會講到「高斯消去法」。而高斯消去法具體是怎麼操作呢?其實就是加減消去法的系統化應用而已:
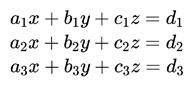
先列出方程組。
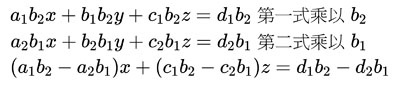
高斯消去法的第一步:消元。這裡示範先消除y。
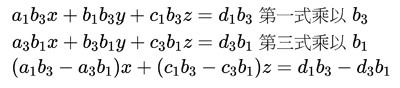
要做兩次,因為消元後剩下兩個未知數因此仍無法直接求解,需要兩個條件因此要做兩次。
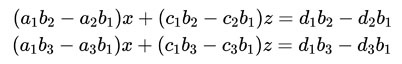
將條件並列,再做一次消元的動作。這次示範消除z。
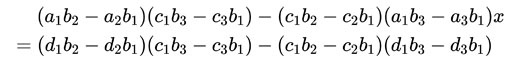
其實整個做法一樣就是加減消去法,只是換個名字而已。
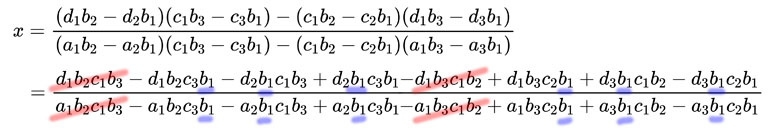
展開。把重複項消掉,剩下來的項又都有 b1 這個共同係數所以可以約分,於是:
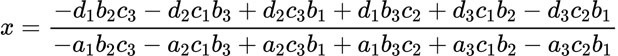
比較一下:
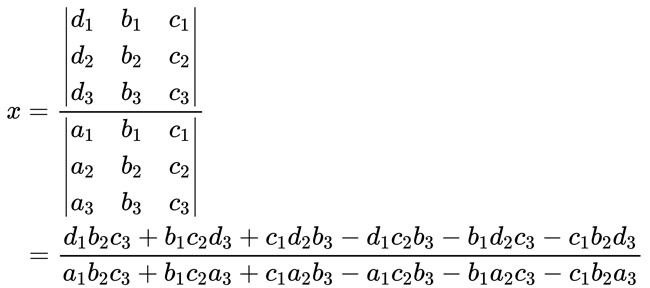
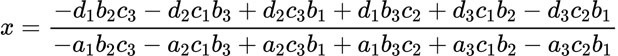
不能說十分相像只能說一模一樣。分子分母都差一個負號結果負負得正,至於項目排列的交換律問題甚至都不需要解釋了。
當然,計算過程要一直乘開,最大需要四個係數乘在一起,看起來計算量反而比行列式要大了。但實際解題過程中並不會碰到要直接把四個係數乘在一起的情況,因為實際代入數值的時候,能化簡自然就會化簡了。
所以總而言之,不管是克拉瑪公式還是高斯消去法,到頭來都只是加減消去法的延伸。這也是亞夜說:方程組只要學會加減消去法就足夠了。
行列式的化簡:
高中學行列式的時候會教「化簡」。因為高階行列式無法直接求解,必須透過降階逐次降到變成二階行列式後才能進行計算。所以儘管以代數形式表示時看起來亂七八糟,但實際求解時可以用一些技巧來節省計算量。
※三階行列式所謂的公式,上面也演示過,其實也只是降階後的必然結果而已。四階以上的行列式有沒有公式?有喔,但相信亞夜,你不會想背的。
首先,行列式因為是對角線方向乘,所以你按照對角線的方向鏡射的話,其值不變:
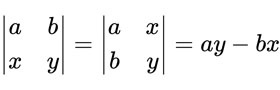
然後,行列式把某行或某列乘以 k 倍後加入另一行(不能是自己),其值也不變:
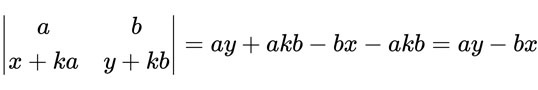
知道這兩個性質後,在解高階行列式時就很方便。怎麼說?因為你必須要先行降階,而降階的方式是選定一行或一列為係數,並乘以餘元素組成的行列式。那麼,如果能夠造出「0」來,計算起來不就方便了嗎?因為 0 乘以任何數都是 0,也就意味著連算都不用算。
那我們怎麼造出 0 來呢?大概是這樣:
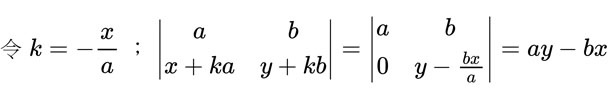
這個動作叫什麼?阿不就「加減消去法」?
我們來看看實際應用:
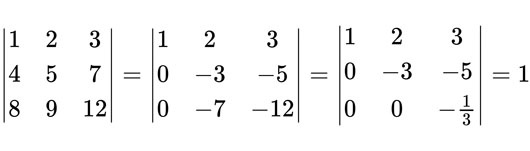
具體做法:
第一行乘以 -4 加到第二行;同時第一行乘以 -8 加到第三行。
接著新的第二行乘以「負三分之七」加到第三行。
這樣只需要計算一條對角就好了,因為其他項都會「乘到 0」。因此答案為 1。
如果暴力做的話:
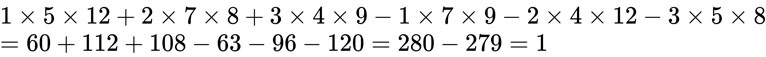
相較之下,暴力做好像沒有比較聰明。咱使用「加減消去法」化簡還比較快,可不是嗎?
那麼再回到上面的務實應用,高斯消去法解三元方程組看似複雜,但你只需要進行「三次」加減消去法就能求出一個未知數。求出未知數後再代入原式就能化簡成二元方程組。此時只要再進行「一次」加減消去法就能再求出另一個未知數,接著答案就求出來了。
而使用克拉瑪公式的話,你有四組行列式要計算。除非題目係數很特殊,不然暴力算太容易按錯了,可不是嗎?所以原則上一樣會透過「加減消去法」去進行化簡,那麼,每一組行列式要進行「三次」加減消去法,合計是 12 次,真的有比較好做?
【結論】
老實說,敝人並不反對背公式。一些常用的東西,背起來真的會比較方便。例如一元二次方程式的求根公式就是,因為太常用了。因式分解法的適用範圍太侷限、十字交乘法要求學生對數字的敏感性、配方法雖然是泛用性最廣的解析性解法,但配方法解出來的結果就是求根公式,既然如此,直接套公式,就不需要每次都經過配方的步驟,這跟九九乘法表一樣,是節約計算量並減少錯誤的有用工具。
可是多元一次方程組不太一樣。你不太會看到誰在那背公式的,因為真的是用不到。最終來說,都會回歸到加減消去法,你變不出新花樣。說真的,如果能有什麼新花樣出來,就不會發展幾百年了大家卻還在用加減消去法,因為它已經是解題方式的頂點了。
克拉瑪公式說是公式,不如說是剛好有這個性質,而且表達式足夠漂亮。基於「美感」,所以好像有必要講一下。然而數學課不是美術課,這種對於「美」的追求留給有興趣的學生去選修就好,至於必須交給學生的那得是真正實用的「工具」才行。所以為什麼敝人反對課綱裡硬要把克拉瑪公式放到必修課裡。
好吧……這東西出現在數學甲裡面,對於社會組來說的確不是必修,但對於自然組而言,克拉瑪好像也沒有那麼重要就是了。
所以怪不得亞夜不是理學院出身的。「實用思維」是典型的工科思維,這天生就是工學院的命啊。

封面圖片:艾蓮老師……等等,妳是教英文的不是數學啊
本篇使用的方程式編輯素材來自:LaTeX公式編輯器

