題目連結:
題目意譯:
給定一個 n × n 個二元矩陣 grid,回傳矩陣中最短通暢路徑之長度。如果沒有通暢路徑存在,則回傳 -1。
一個二元矩陣中的一條通暢路徑為一條從最左上角的格子(即 (0, 0))到最右下角的格子(即 (n - 1, n - 1))之路徑,使得
所有路徑上經過的的格子之值皆為 0。
所有相鄰格子為八方向相鄰(即兩格子相異且共享一個頂點或是一條邊)。
通暢路徑之長度為這個路徑上經過的格子數。
限制:
n == grid.length
n == grid[i].length
1 ≦ n ≦ 100
grid[i][j] 只會是 0 或是 1
範例測資:
範例 1:
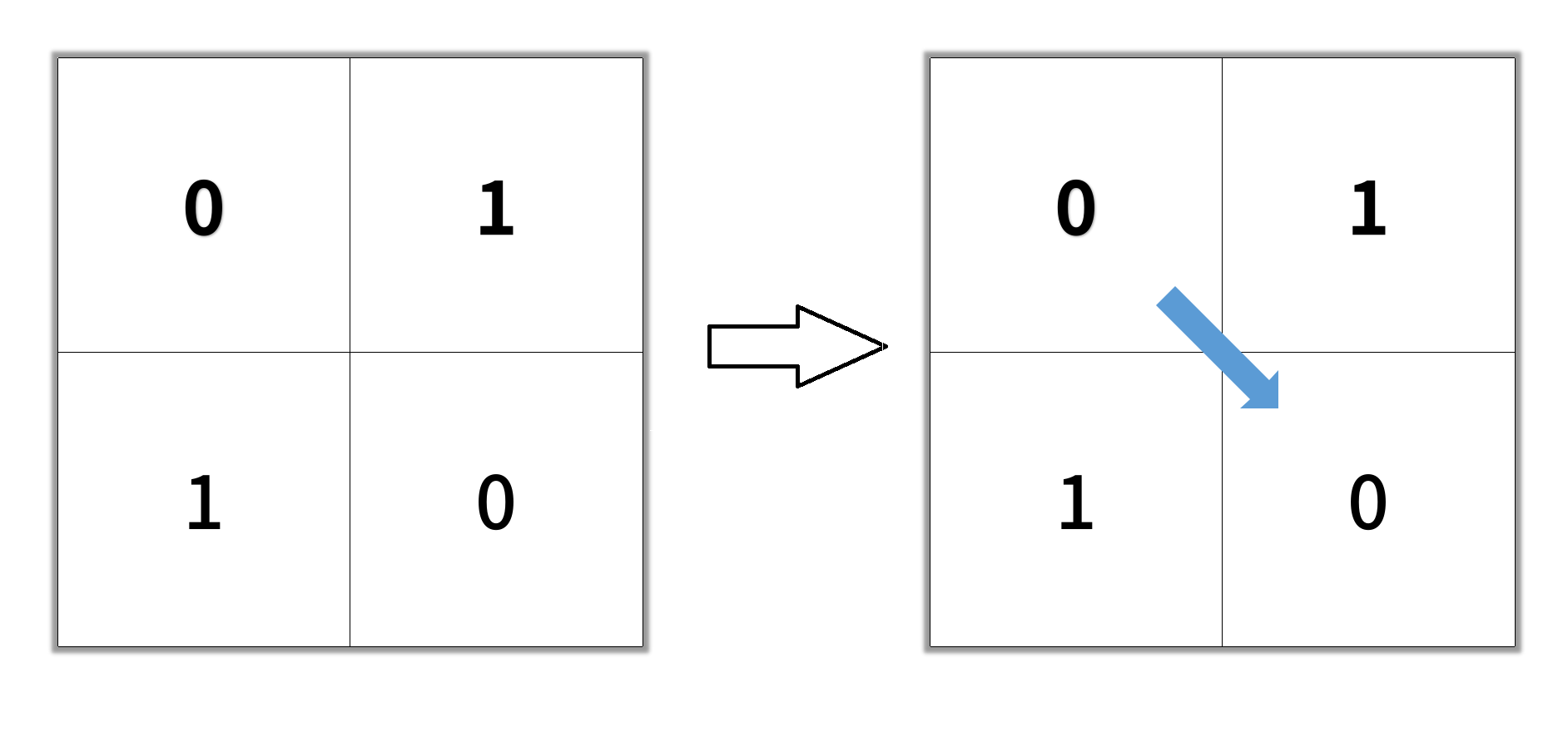
輸入: grid = [[0,1],[1,0]]
輸出: 2
範例 2:
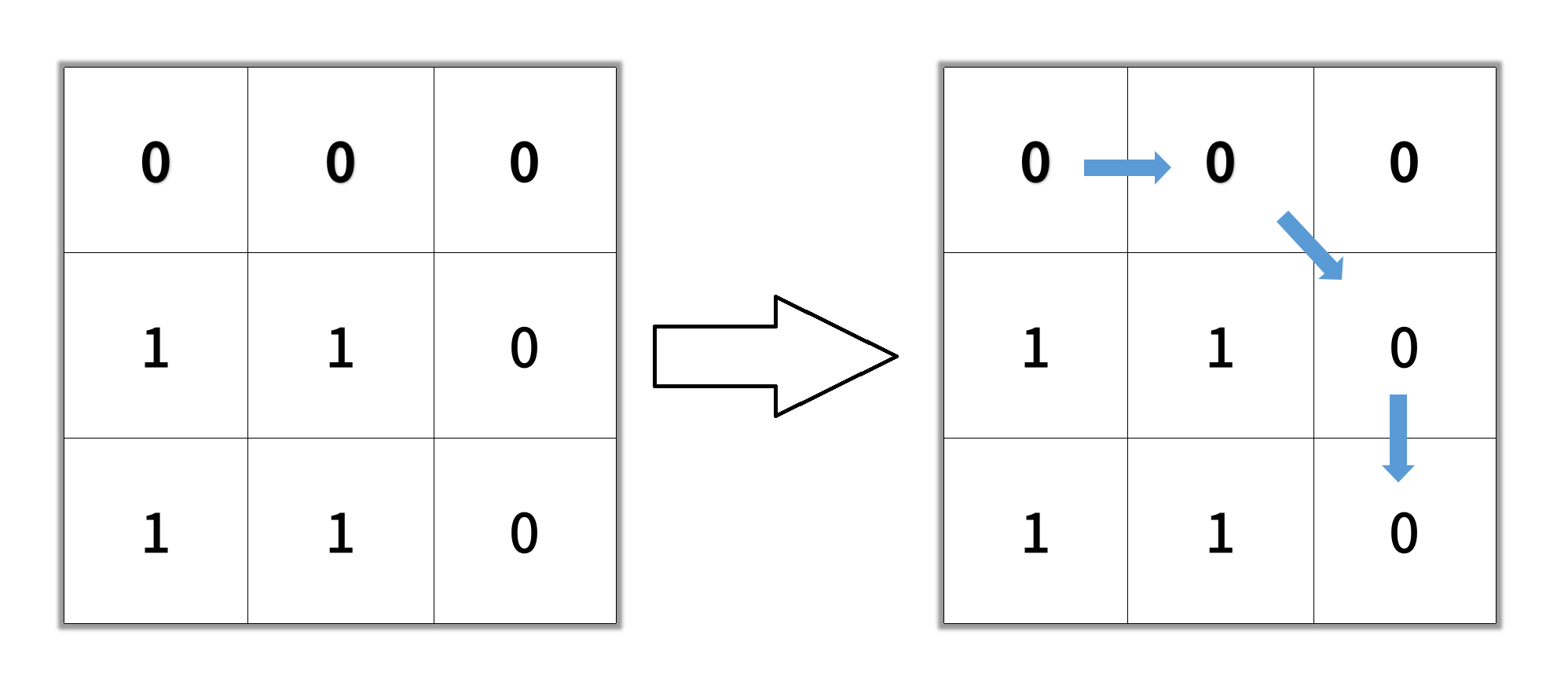
輸入: grid = [[0,0,0],[1,1,0],[1,1,0]]
輸出: 4
範例 3:
輸入: grid = [[1,0,0],[1,1,0],[1,1,0]]
輸出: -1
解題思維:
其實就是走迷宮題型(如
這題)之變體,只是現在有八個方向可走到別的格子,而且任何值非零的格子都是「牆壁」、值為零的格子才是「路」。
此次分享到此為止,如有任何更加簡潔的想法或是有說明不清楚之地方,也煩請各位大大撥冗討論。