題目連結:
題目意譯:
給定一個二元樹
struct Node {
int val;
Node *left;
Node *right;
Node *next;
}
將每個指標 next 都填上其所屬節點右側的「下一個」節點。如果右側的下一個節點不存在,則指標 next 應設為 NULL。
一開始,所有指標 next 都被設成 NULL。
限制:
樹中的節點數位於範圍 [0, 6000] 中。
-100 ≦ Node.val ≦ 100
你只能使用常數額外空間。
遞迴的方式是可被接受的。你可以假設在本題中隱含的堆疊空間不算作額外空間。
範例測資:
範例 1:
輸入: root = [1,2,3,4,5,null,7]
輸出: [1,#,2,3,#,4,5,7,#]
解釋: 給定上圖的完美二元樹(圖 A),你的函式應將每個指標 next 都指向其右側的下一個節點,如圖 B 所示。序列化的輸出為階層探訪(Level order),其中每一層是由指標 next 們連接在一起,而 '#' 則用來標示每一層的結尾。
範例 2:
輸入: root = []
輸出: []
解題思維:
跟
昨天的題目很像,但是現在給定的樹不一定是完美二元樹了。也就是說每個節點的小孩數量不再僅限於 0 或是 2,而且所有葉節點不一定位於同一層上。
觀察下圖:
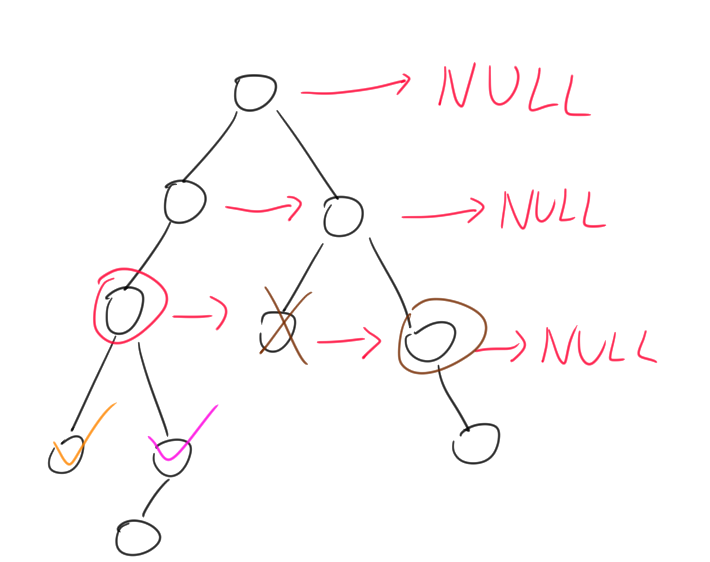
可以看到原本在完美二元樹中,紫色勾勾的節點的 next 應指向紅色圈圈的 next 指向的節點(如果該節點不是 NULL)之左小孩。但是現在可以看到棕色叉叉的節點沒有任何小孩,因此我們應該繼續往棕色叉叉的 next 之指向,也就是棕色圈圈的節點。而這個節點有一個右小孩,因此紫色勾勾節點的 next 應指向這個節點才對。
而正因如此,現在遞迴的順序變得很重要了,因為如果我們在根節點先往左子樹遞迴的話,就無法知道右子樹的那些紅色箭頭之指向。因此昨天的遞迴程式虛擬碼變成了:
Connect(*nowNode, *sibling)
if nowNode == NULL
return
nowNode->next = sibling
while siblings AND siblings->left == NULL AND siblings->right == NULL && siblings->next != NULL
siblings = siblings->next;
if siblings != NULL
if siblings->left != NULL
siblings = siblings->left
else
siblings = siblings->right
if nodeNode->right != NULL
Connect(nowNode->right, siblings)
Connect(nowNode->left, nowNode->right)
else
Connect(nowNode->left, siblings)
一樣,我們只需要呼叫 Connect(root, NULL) 便可以完成遞迴地完成所有紅色箭頭(next)。
此次分享到此為止,如有任何更加簡潔的想法或是有說明不清楚之地方,也煩請各位大大撥冗討論。