題目連結:
題目意譯:
給定一個連結串列(Linked List)的開頭 head,回傳環開始的節點。如果環不存在,則回傳 null。
如果串列中有存在一些節點可以藉由一直跟著指標 next 走而重複抵達的話,則代表該連結串列中有環。測資中,pos 將代表尾端連結到的連結串列中之位置(索引值從 0 開始)。如果 pos 為 -1 ,則連結串列中無環。注意到,pos 實際上並不會作為參數傳入。
請勿修改連結串列中的內容。
限制:
串列中的節點數量位於範圍 [0, 10 ^ 4] 中。
-10 ^ 5 ≦ Node.val ≦ 10 ^ 5
pos 為 -1 或是一個串列中的合法索引值。
進階:你可以使用 O(1)(即,常數大小)的記憶體解決本題嗎?
範例測資:
範例 1:
輸入: head = [3,2,0,-4], pos = 1
輸出: 尾端連到索引值 1 的節點(原文如此。譯者注:也就是我們應回傳索引值 1 的那個節點本身)
解釋: 連結串列中有環,其中尾端連到第二個節點。
範例 2:
輸入: head = [1,2], pos = 0
輸出: 尾端連到索引值 0 的節點
解釋: 連結串列中有環,其中尾端連到第一個節點。
範例 3:
輸入: head = [1], pos = -1
輸出: 無環(原文如此。譯者注:這邊實際上回傳的東西跟語言有關,例如 C++ 應回傳 NULL 或是 nullptr)
解釋: 連結串列中沒有環。
解題思維:
跟這系列
第一題很像,只是現在要找環的開始位置。這邊,我們使用第一題所提及的 Floyd 判圈演算法(Floyd Cycle Detection Algorithm,也稱龜兔賽跑算法,即 The Tortoise and the Hare Algorithm),詳情請回到第一題的鏈結查看。
不過問題是上面這個演算法中,T 和 H 相遇時會停在串列中的何處(如果有環的話)呢?而這實際上跟這演算法為何可以在線性時間內找到環有些許的相關,因此順便證明此演算法的時間複雜度是線性:
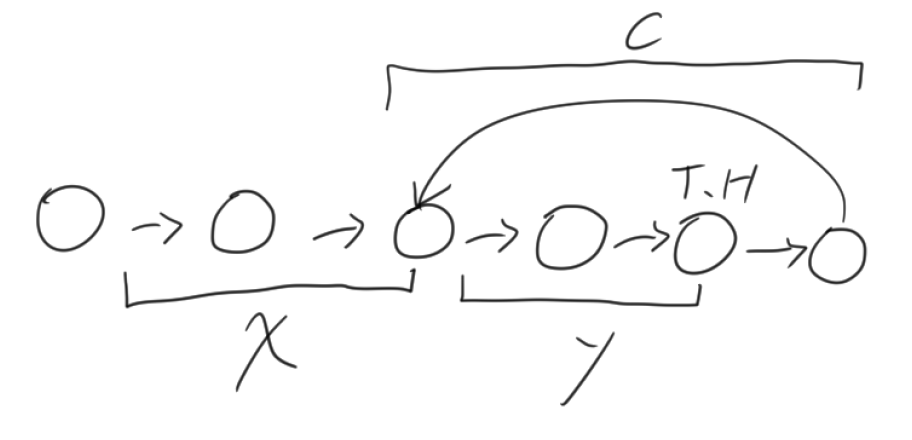
假設 X 是從開頭到循環節開始所需經過的節點數(不含開頭)、Y 是從循環節開始到 T 和 H 之會合節點所需經過的節點數(不含開始)以及 C 為循環節的長度(節點數),如下圖所示:
可以看到 T 、 H 會各自在 X 和 X ÷ 2 步之後踏入到循環節當中。此時 H 和 T 最差有可能會是 H 在 T 前面一個節點的位置(除非頭尾相連,此時 X = 0 且 H 和 T 距離也是 0。但是因為還沒繞過一圈,所以無從得知),但是由於 H 跑得是 T 的兩倍快所以實際上需要再 C - 1 步彼此才能碰面。
因此這個演算法的時間複雜度即為 O(X) + O(C) = O(n),其中 n 為串列中節點的個數,也就是線性的時間複雜度。
接著再假設 H 移動時經過總節點數(不含開頭)為 X + Y + f × C,而 T 則為 X + Y + s × C。其中 s 和 t 為非負整數。會假設 s 和 t 是因為有可能循環節非常地短,而前面的部分很長。因此兔子 H 有可能會需要在循環節繞很多圈才能等到烏龜 T 進到圈子來。
而由於 H 的移動速度為 T 的兩倍,因此可以得到
X + Y + f × C = 2(X + Y + s × C)
移項一下可得
(f - 2s) × C = X + Y
而 f - 2s 是一個正整數(只要有環的話),因此我們可以將等號左邊寫為
qC = X + Y
其中 q 是一個某個正整數。
此時我們回到上面的示意圖。當 T 和 H 在循環節中碰面後,如果我們把其中一個傢伙(例如說 T,因此 H 則留在原地)放回到串列的開頭,然後令 T 和 H 以同樣的速度(每次前進一個節點)往前迭代。則我們可以看到它們將會在循環節開頭再次碰面。
然而這並不是巧合,因為根據上面我們得到的等式移項可以之後得到
X = qC - Y
而這代表的意義是:留在原地的 H 距離循環節開頭是 Y,而如果我們讓 H 去多走 qC - Y 個節點此時「總距離」變成了 Y + (qC - Y) = qC 因此會回到循環節開頭。但是正因為 X = qC - Y,因此放回到開頭的 T 也會剛好抵達循環節的開頭。因此彼此碰面是必定會發生的,不論 X 、 Y 、 C 實際上是多少,只要有環就會發生。
因此我們可以在使用 Floyd 判圈演算法之後,如果無環就回傳空指標;反之則將 T 或 H 中的其中一者放回到串列開頭,然後令 T 、 H 同時按照每步走一個節點的速度向前直到會合為止。此時便可以找到循環節開頭,該節點即是所求。
此次分享到此為止,如有任何更加簡潔的想法或是有說明不清楚之地方,也煩請各位大大撥冗討論。