題目連結:
題目意譯:
你被給定一陣列 seats 代表著一列的座位,其中 seats[i] = 1 代表著有一個人正坐在第 i 個座位而 seats[i] = 0 代表著第 i 個座位是空的(索引值從 0 開始)。
至少會有一個空座位存在�����,而且至少有一個人會坐在某個座位上�。
Alex 想要坐在某個特定的座位上使得他和與他最近的人之間的距離是最大化的。
回傳這個與最近的人之最大距離值。
限制:
2 ≦ seats.length ≦ 2 × 10 ^ 4
seats[i] 只會是 0 或是 1�����。
至少有一座位是空的����。
至少有一座位有坐人。
範例測資:
範例 1:
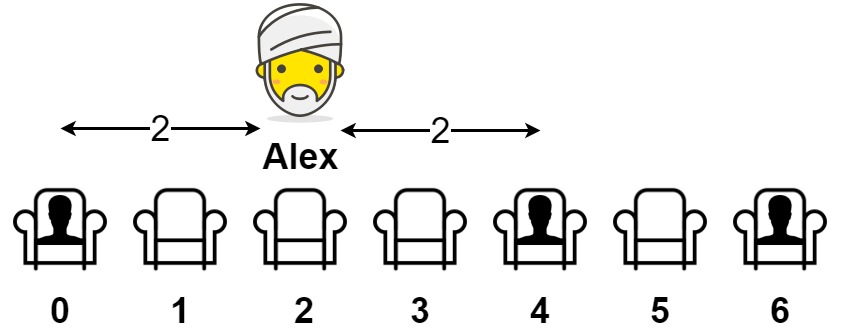
輸入: seats = [1,0,0,0,1,0,1]
輸出: 2
解釋:
如果 Alex 坐在第二個空位上(即 seats[2]),則最近的人將會是 2 個座位遠。
如果 Alex 坐在其他的空位上,則最近的人將會是 1 個座位遠。
因此離最近的人之距離為 2�����。
範例 2:
輸入: seats = [1,0,0,0]
輸出: 3
解釋:
如果 Alex 坐在最後一個座位(即 seats[3])�����,則最近的人將會是 3 個座位遠。
而這是可能的最大距離����,因此答案為 3���。
範例 3:
輸入: seats = [0,1]
輸出: 1
解題思維:
單純地掃過 seats 中所有的「1」�,然後去看每兩個相鄰的「1」(也就是中間沒有其他的「1」)之間的距離一半之值(因為坐在中間距離是最遠的)����。之後再與第一個「1」的左側以及最後一個「1」的右側去比對。因為對於前者�,Alex 可以坐在第一個空位(如果可以的話)便可以與前者離得最遠����;同理對於後者��,Alex 可以坐在最後一個座位����。
將上面所有看到的距離值取其中的最大值即是所求�。
此次分享到此為止,如有任何更加簡潔的想法或是有說明不清楚之地方�����,也煩請各位大大撥冗討論�����。