題目連結:
題目意譯:
你被給定一個 m × n 整數矩陣 grid,其中 m 和 n 皆為偶數,以及一整數 k。
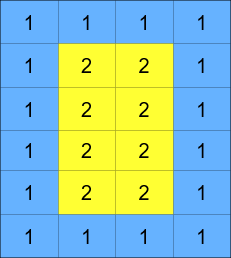
矩陣由好幾層組成,如下圖所示,其中每種顏色代表一層:
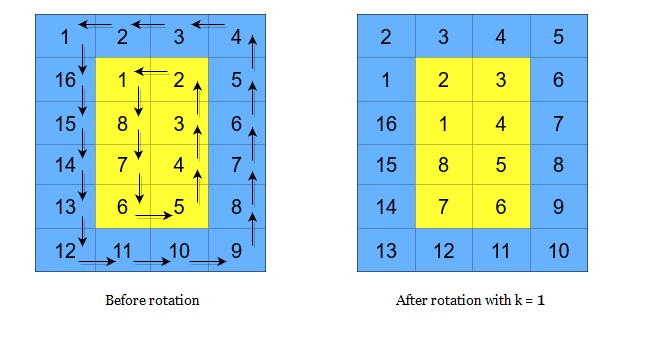
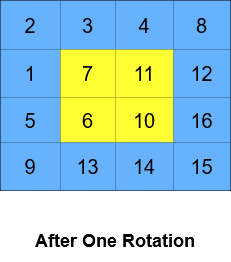
一次的矩陣之循環旋轉會將矩陣中每一層循環地轉一次。在一次循環地旋轉一層之中,於該層之中每個元素將取代其逆時針方向之相鄰元素。一旋轉範例如下:
回傳經由 k 次循環旋轉後的矩陣。
限制:
m == grid.length
n == grid[i].length
2 ≦ m 、 n ≦ 50
m 和 n 都是偶數。
1 ≦ grid[i][j] ≦ 5000
1 ≦ k ≦ 10 ^ 9
範例測資:
範例 1:
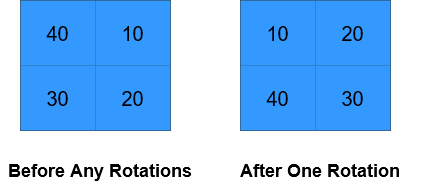
輸入: grid = [[40,10],[30,20]], k = 1
輸出: [[10,20],[40,30]]
解釋: 上圖顯示了每個狀態時的 grid。
範例 2:
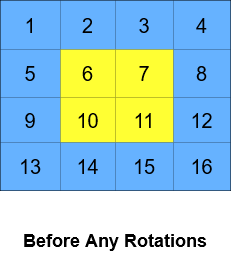
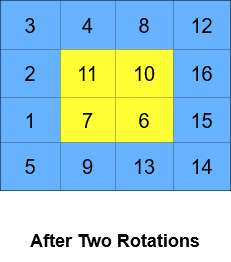
輸入: grid = [[1,2,3,4],[5,6,7,8],[9,10,11,12],[13,14,15,16]], k = 2
輸出: [[3,4,8,12],[2,11,10,16],[1,7,6,15],[5,9,13,14]]
解釋: 上圖顯示了每個狀態時的 grid。
解題思維:
可以看到,矩陣所擁有的層數為 min(m, n) ÷ 2 層。因此我們可以窮舉出每一層的最左上角為 (0, 0) 、 (1, 1) 、……,其中 (r, c) 代表第 r 列第 c 行(索引值從 0 開始)。
對於每一層 (i, i) 我們可以計算出水平長度為 H = n - 2i 、 鉛直長度為 V = m - 2i。則該層四個角落(左上、右上、右下、左下角)依序為 (i, i) 、 (i, i + H - 1) 、 (i + V - 1, i + H - 1) 和 (i + V - 1, i)。
然後我們從左上角開始依序走過其他節點,把該層的「數列」擷取出來。假設該數列長度為 X,則我們可以看到每旋轉一次本層的數字該數列就會往左旋轉一個位置(如
這題的旋轉,只是方向相反)。而我們可以看到每旋轉 X 次,數列就會回到原本的樣子。因此旋轉 k 次,實際上對於本層而言只旋轉了 k % X 次(「%」代表取餘之操作)。
因此我們可以將擷取出來的數列往左旋轉 k % X 個位置,然後將這個新的數列塞回到矩陣之中(怎麼擷取的就怎麼塞回去)。
因此對於每一層都做過這樣子的判斷和動作後,整個矩陣便按照題目的要求旋轉了 k 次。
此次分享到此為止,如有任何更加簡潔的想法或是有說明不清楚之地方,也煩請各位大大撥冗討論。