題目連結:
題目意譯:
這裡有著 n 個小孩排成一列。每個小孩被分配到一個評分值其給定於整數陣列 ratings。
你正要給這些小孩一些糖果,其滿足以下要求:
每個小孩至少要有一個糖果。
有著較高評分值的小孩應得到比其鄰居更多的糖果。
回傳分發給這些小孩所需的最少糖果數。
限制:
n == ratings.length
1 ≦ n ≦ 2 × 10 ^ 4
0 ≦ ratings[i] ≦ 2 × 10 ^ 4
範例測資:
範例 1:
輸入: ratings = [1,0,2]
輸出: 5
解釋: 你依序分配給第一、第二和第三位小孩 2 、 1 、 2 個糖果。
範例 2:
輸入: ratings = [1,2,2]
輸出: 4
解釋: 你可以依序分配給第一、第二和第三位小孩 1 、 2 、 1 個糖果。
第三個小孩只得到一個糖果,因為這樣便可以滿足上面兩個條件。
解題思維:
首先可以看到我們可以從評分值最小的開始發放糖果。
對於某個小孩 rating[i],我們先發放 1 個糖果(因為至少要有 1 個),然後看該名小孩的左右是否已經被發過糖果了。如果左右有人被發過糖果的話,則代表那些小孩的評分值 ≦ 當前小孩的評分值。
而如果那些小孩的評分值 < 當前小孩的評分值,則根據提議我們應當分配給當前小孩比那些小孩更多的糖果。而因為要最小化發放的糖果,因此當前小孩所分配到的糖果數為那些小孩的最大糖果數 + 1。
可以看到時間複雜度會是 O(n log(n))(因為要將評分值排序),其中 n 為小孩的個數。但是,我們可以把時間降低至 O(n)。
稍微觀察可以發現:所有的評分值為「局部低點」(左右兩邊的評分值皆大於自己)或「平坦處」(左右兩邊的評分值與自己相同)之小孩都將只會被分配到一個糖果。
例如 [1,2,3,4,7,6,9,9,9] 中的「1」(端點也算在內)和「6」算做局部低點,而最後的兩個「9」則算「平坦處」。而實際上:
評分值:[1,2,3,4,7,6,9,9,9]
糖果數:[1,2,3,4,5,1,2,1,1]
可以再進一步看到像是 [1,2,3,4,7] 這種遞增數字片段的糖果數也是從 1 開始逐漸遞增;同樣地,遞減片段也會遞減(反過來看就是跟遞增片段一樣,則低點遞增)。
因此我們觀察以下測資可以看到:
當「上升段」連接著「準平坦處」(代表某數的左右只有一者與它相同)時,例如 [2,5,7,7],上升段的糖果數將從低點為 1 開始遞增到準平坦處為止。
當「下降段」連接著「準平坦處」時,例如 [5,4,3,3],下降段將從準平坦處為 1 開始往回(即向左)遞增到高點(但是高點本身可能會被高點前的上升段長度影響,所以此時需取糖果數最大值看哪段的結果最大,例如 [1,3,4,5,4,3,3] 的「5」)或另一個準平坦處。
當「下降段」連接著「上升段」時,例如 [7,4,1,3],下降段將從準平坦處為 1 開始往回遞增到高點(一樣會有如上的問題)或另一個準平坦處。
當「上升段」連接著「下降段」時,例如 [1,3,4,5,4],此時會有如上的高點之糖果數問題,因此可以留給接下來的下降段的時候再一起判斷。
當遇到「平坦處」時,則糖果數為 1。
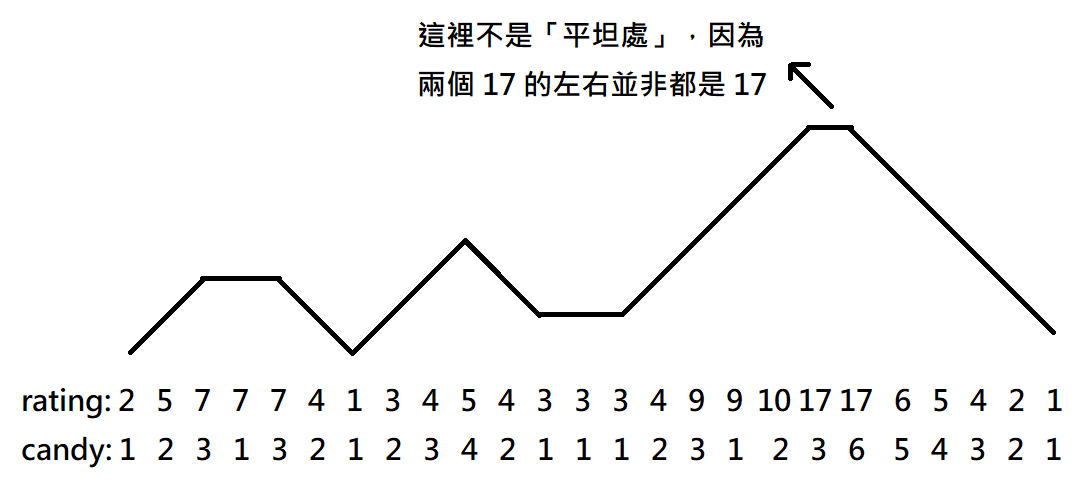
因此,我們可以直接掃過陣列,記錄前一刻以及現在的上升下降之情形(以及這些片段的長度),並根據以上狀況去計算應有的糖果數。因此時間可以降為 O(n)。
此次分享到此為止,如有任何更加簡潔的想法或是有說明不清楚之地方,也煩請各位大大撥冗討論。