題目連結:
題目意譯:
給定兩個 n × n 二元矩陣 mat 和 target ,回傳真(True)如果可以藉由逐漸地旋轉 mat 90 度來使 mat 等於 target ;反之,回傳假(False)。
限制:
n == mat.length == target.length
n == mat[i].length == target[i].length
1 ≦ n ≦ 10
mat[i][j] 和 target[i][j] 只會是 0 或是 1 。
範例測資:
範例 1:
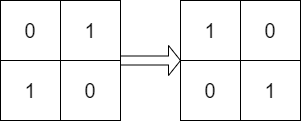
輸入: mat = [[0,1],[1,0]], target = [[1,0],[0,1]]
輸出: true
解釋: 我們可以旋轉 90 度使 mat 等於 target 。
範例 2:
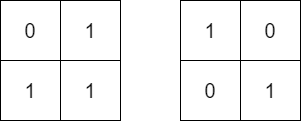
輸入: mat = [[0,1],[1,1]], target = [[1,0],[0,1]]
輸出: false
解釋: 不可能藉由旋轉 mat 來使 mat 等於 target 。
範例 3:
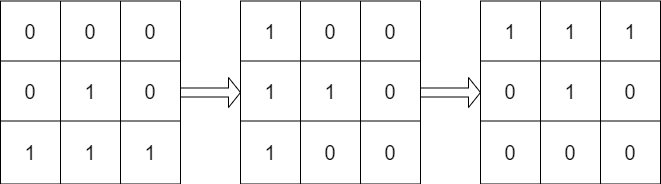
輸入: mat = [[0,0,0],[0,1,0],[1,1,1]], target = [[1,1,1],[0,1,0],[0,0,0]]
輸出: true
解釋: 我們可以旋轉 90 度兩次使 mat 等於 target 。
解題思維:
利用
這題的想法,將四種可能的旋轉位置(不動、旋轉 90 度、旋轉 180 度和旋轉 270 度)之陣列 mat 去和 target 比較。如果有任何一者相等,則回傳真。如果四個都不行則代表不可能使 mat 等於 target ,因此回傳假。
此次分享到此為止,如有任何更加簡潔的想法或是有說明不清楚之地方,也煩請各位大大撥冗討論。