達人專欄 對我來說，這大概是我寫過有史以來最困難的一篇文了，畢竟 RSA 加密算法牽涉到即使已經(jīng)修完高中數(shù)學(xué)都不見得能夠理解的前備知識，特地寫成一篇也是為了逼迫自己掌握它的觀念，試試看能不能成功讓一般人也能理解 RSA 加密算法。
本文算式圖片設(shè)計以深色模式為主，閱覽前建議切換為深色模式。由於手機 App 在切換樣式前需要強制重啟 App，若你是日間模式使用者，請在切換前利用「收藏」功能，避免切換完模式以後找不回本文。
。加密演算法的對稱性
以前我曾經(jīng)在《壓縮檔如何幫你的檔案加密？有可能「繞」過去嗎？》提到，RC4 加密算法利用了邏輯閘 XOR 的基本性質(zhì)：
「若計算 A XOR B 得到 C，則計算 C XOR B 必定會得到 A」
這樣的性質(zhì)，讓我們能夠把一組數(shù)據(jù)和一組密鑰變換成無法直接解讀的密文，等到我們需要使用的時候，再用同樣一組密鑰把密文變換回來就可以了，這就是所謂的「對稱式加密」。
最常見的應(yīng)用就是壓縮檔（AES-256 加密演算法）。我們向特定對象分享敏感資料的時候，為了避免這些檔案因為各種疏失而被其他人取得後輕易打開，通常都會用一組密碼把它加密，之後才把檔案傳過去。
然而，使用這種方式時，你和對方必須事先共同約定好一組密鑰，要是在決定並且分享密鑰給對方的過程中，被人竊聽了、散播出去了，那麼這些加密的保護也只是徒勞。
因此，在資訊領(lǐng)域裡發(fā)展出了「非對稱性加密」的技術(shù)——加密的時候使用一組密鑰、解密的時候使用另一組密鑰，我們甚至可以把其中一組密鑰公開出去給所有人知道也沒關(guān)係！這聽起來非常不可思議，而其中的代表正是今天的主角：1977 年發(fā)明的 RSA 加密演算法。
我們用特定的方法產(chǎn)生出一對存有一定關(guān)係的密鑰：公鑰（Public Key）、私鑰（Private Key），其中公鑰用來加密資料，私鑰拿來解密資料。
因為公鑰和私鑰之間的數(shù)學(xué)關(guān)係非常複雜，所以即使讓大家知道了公鑰，這些人也難以藉此推導(dǎo)出對應(yīng)的私鑰，再加上私鑰只需要自己保管而不需要傳遞給任何人，自然也就保證了第三方無法輕易地破譯出原文內(nèi)容。
。RSA 加解密的實例
先不要談公鑰和私鑰如何產(chǎn)生，因為那是 RSA 最複雜的部分。我們要先知道 RSA 的密鑰必須合乎 RSA 演算法的規(guī)範，經(jīng)過特定的流程會產(chǎn)生出三個數(shù)字：N、e、d，各自作為密鑰的一部分。
其中數(shù)對 (N, e) 是公鑰，而 (N, d) 是私鑰。
先來講它的加解密過程吧，我們會需要用到。
假設(shè)我現(xiàn)在產(chǎn)生了一組密鑰，然後有一組數(shù)據(jù)需要被加密：
公鑰：(65, 35)
私鑰：(65, 11)
原文：[63, 34, 27, 14, 50, 2, 21, 17]
接下來我們計算：
63 的 35 次方，再除以 65，得到餘數(shù)為 32
34 的 35 次方，再除以 65，得到餘數(shù)為 44
27 的 35 次方，再除以 65，得到餘數(shù)為 53
14 的 35 次方，再除以 65，得到餘數(shù)為 14
50 的 35 次方，再除以 65，得到餘數(shù)為 45
2 的 35 次方，再除以 65，得到餘數(shù)為 33
21 的 35 次方，再除以 65，得到餘數(shù)為 31
17 的 35 次方，再除以 65，得到餘數(shù)為 23
那就得到密文是 [32, 44, 53, 14, 45, 33, 31, 23] 了
反過來，持有私鑰 (65, 11) 的我，可以用同樣的方法恢復(fù)原文，計算：
32 的 11 次方，再除以 65，得到餘數(shù)為 63
44 的 11 次方，再除以 65，得到餘數(shù)為 34
53 的 11 次方，再除以 65，得到餘數(shù)為 27
14 的 11 次方，再除以 65，得到餘數(shù)為 14
45 的 11 次方，再除以 65，得到餘數(shù)為 50
33 的 11 次方，再除以 65，得到餘數(shù)為 2
31 的 11 次方，再除以 65，得到餘數(shù)為 21
23 的 11 次方，再除以 65，得到餘數(shù)為 17
成功恢復(fù)出原文 [63, 34, 27, 14, 50, 2, 21, 17]。
也就是說，如果我打算接收對方傳來的敏感訊息，那麼我可以產(chǎn)生一對公鑰 (65, 35) 和私鑰 (65, 11)，並且事先告訴對方：「在你要傳達訊息給我以前，請先使用公鑰 (65, 35) 把訊息加密。」
在此同時，已經(jīng)產(chǎn)生的私鑰 (65, 11) 就自行妥善保管，從頭到尾都不讓任何人知道。當(dāng)對方把加密後的密文傳送過來，我們只要利用保留在身上的這對私鑰 (65, 11)，就可以還原出對方的訊息了。
當(dāng)然，這個計算過程產(chǎn)生的數(shù)是非常恐怖的，像是計算 50 的 35 次方會得到一個 60 位數(shù)的超大數(shù)字，所以在電腦裡也通常會用一些方式去優(yōu)化、簡化這些過程，避免在加密、解密的過程耗費太多時間。
。RSA 的密鑰產(chǎn)生過程
如果明文（Plaintext）是 P、密文（Ciphertext）是 C，我們可以表達為：
RSA 產(chǎn)生金鑰的步驟如下：
1. 自行挑選兩個質(zhì)數(shù) p、q，把兩數(shù)相乘得到 N
2. 計算 φ(N)，得到 r
3. 尋找一個同時符合以下兩條件的數(shù) e：
(1) 1 < e < r
(2) e 與 r 互質(zhì)
4. 尋找一個數(shù) d，符合「ed ≡ 1 (mod r)」的條件
5. 得到的 (N, e) 為公鑰，(N, d) 為私鑰
我們可以實作一次：
1. 挑選兩個質(zhì)數(shù) p=5, q=13，相乘得到 N=65
2. 計算 φ(N)，φ(65) = φ(5)φ(13) = 4×12，取名為 r，得到 r=48
3. 找到一個 e=35 符合「1 < e < r」而且「公因數(shù) (35, 48) = 1」
4. 找到一個 d=11，符合「ed 除以 r 得到餘數(shù)為 1」（385÷48=8...1）
5. 得到 (65, 35) 為公鑰，(65, 11) 為私鑰
。RSA 的前備知識
說到原理層面就開始複雜起來了，這也是我花最多時間消化的地方。在開始講原理以前，必須要有兩個前備知識，一個是歐拉函數(shù)，一個是費馬小定理。
首先講歐拉函數(shù)。數(shù)學(xué)家歐拉曾經(jīng)研究了一個函數(shù) φ(n)，這個函數(shù)簡單來說就是「求得 1~n 之間和 n 互質(zhì)的數(shù)字個數(shù)」。比如在 6 這個數(shù)底下只有 1, 5 兩個數(shù)和 6 互質(zhì)，所以 φ(6)=2；在 21 底下有 1, 2, 4, 5, 8, 10, 11, 13, 16, 17, 19, 20 一共 12 個數(shù)字跟 21 互質(zhì)，所以 φ(21)=12。
但如果今天 n 是一個質(zhì)數(shù)，我們知道像 13 這個數(shù)字，在它底下 1~12 每個數(shù)字都跟 13 互質(zhì)，不可能會有其他的公因數(shù)，所以我們可以知道在 n 是質(zhì)數(shù)的狀況下 φ(n) = n-1。
另一方面，歐拉函數(shù)有個特性，就是如果 m、n 互質(zhì)，那麼 φ(mn) = φ(m)φ(n)，這也是為什麼產(chǎn)生金鑰的時候 φ(N) = φ(pq) = φ(p)φ(q) = (p-1)(q-1) 了。
接下來便是真正的核心。1636 年，費馬發(fā)現(xiàn)了當(dāng) p 是質(zhì)數(shù)的狀況下：
換個講法也可以說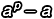 
可以被 p 整除，這正是費馬小定理。一百年後，歐拉正式把費馬小定理證明出來，並且把它拓展成：
可以被 p 整除，這正是費馬小定理。一百年後，歐拉正式把費馬小定理證明出來，並且把它拓展成： 當(dāng) a 和 n 互質(zhì)的情況下，
當(dāng)然同樣也可以換個說法：「若 a 和 n 互質(zhì)，則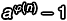 
可以被 n 整除」，這兩件事情是一樣的。
可以被 n 整除」，這兩件事情是一樣的。。實際的 RSA 加解密推導(dǎo)
那麼我們現(xiàn)在再回來看 RSA 的加解密流程：
明文 P、密文 C、公鑰 (N, e)、私鑰 (N, d)、某整數(shù) K
在 RSA 的加密過程，首先我們透過公鑰 (N, e) 加密：
計算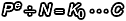 
那我們自然可以把式子表達為：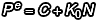
現(xiàn)在，我們必須證明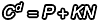 
，因為只有在證明這件事之後才能確保「在使用 e 加密過後，還能使用 d 來順利解密」。
，因為只有在證明這件事之後才能確保「在使用 e 加密過後，還能使用 d 來順利解密」。 先把剛剛加密的式子變換一下，我們知道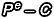 
會得到 N 的某個倍數(shù)，那麼反過來說 
也會是 N 的某個倍數(shù)（只是差了一個負號而已）：
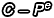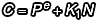
會得到 N 的某個倍數(shù)，那麼反過來說 也會是 N 的某個倍數(shù)（只是差了一個負號而已）： 我們要證明 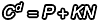，於是兩邊同時作 d 次方：
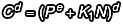
，於是兩邊同時作 d 次方： 我們觀察二項式 (x+y) 的冪次展開，不難發(fā)現(xiàn)除了第一項以外，後面的每一項都有 y 的蹤影：
據(jù)此，我們可以知道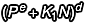 
這個式子展開以後，除了第一項會是 
以外，每一項因為都曾經(jīng)乘過至少一次 
，這些第二項以後的東西既然每個都是 N 的倍數(shù)，那麼加起來就也一定會是 N 的倍數(shù)——所以我們可以乾脆把它寫成 
。
這個式子展開以後，除了第一項會是 以外，每一項因為都曾經(jīng)乘過至少一次 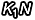，這些第二項以後的東西既然每個都是 N 的倍數(shù)，那麼加起來就也一定會是 N 的倍數(shù)——所以我們可以乾脆把它寫成 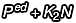。 接下來，我們回去看產(chǎn)生密鑰的過程，可以看到 ed ≡ 1 (mod r) 這件事情，也就是指 ed 除以 r 會得到餘數(shù)為 1，也就是說我們可以說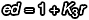 
，那麼剛剛的式子就可以改寫為：
，那麼剛剛的式子就可以改寫為： 提出一個 P：
再回頭對照一下，r 是怎麼來的呢？可以看到 r 是透過 φ(N) 得來的，所以又可以改寫成：
接下來就用到前面講到的費馬小定理了，我們知道 
會是 1 + (N的某個倍數(shù))，所以就能再改成：
會是 1 + (N的某個倍數(shù))，所以就能再改成： 整理：
我們證明了在遵守 RSA 密鑰產(chǎn)生程序得出 N、e、d 三個數(shù)的情況下：
當(dāng)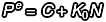 
，則 
，則 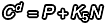也就有：
當(dāng)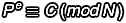 
，則 
，則 這過程的每個 K 都是某個整數(shù)，具體的數(shù)值是多少並不重要，因為我們只在乎計算完以後求得的餘數(shù)而已。
大概就是這樣。至於他們是如何想到可以這麼做，你大概就要去問 Ron Rivest、Adi Shamir、Leonard Adleman 這三個神人了。
。RSA 的安全性
我們從推導(dǎo)過程可以窺見，RSA 的安全性是建立在「質(zhì)數(shù)」上面的。如果我們一開始在產(chǎn)生金鑰時選擇的兩個質(zhì)數(shù) p、q 非常小，那麼嘗試破解的駭客就可以自行產(chǎn)生出用來嘗試的公鑰、私鑰，並且試圖解開這些密文，所以為了避免這種狀況發(fā)生，我們必須在產(chǎn)生金鑰的時候選擇夠大的質(zhì)數(shù)。
這些用來加密的 N、e、d 產(chǎn)生出來以後，如果其他人截取了密文 C，想要從 C 恢復(fù)成明文 P，那麼他們就得先知道 d；如果要取得 d，那麼就得知道 r 的值（也就是 φ(N)）；如果想取得 φ(N) 的值，就得要知道 p 和 q（因為 φ(N) = φ(p)φ(q) = (p-1)(q-1)）；要想知道 p 和 q 的值，就得成功把 N 質(zhì)因數(shù)分解……
這正是 RSA 的安全基礎(chǔ)。想像一下，我們可以很輕鬆地把兩個質(zhì)數(shù) 3389 和 2377 相乘得到 8055653，但要是反過來在你手上只有「8055653」的情況下，我們就難以把它短時間內(nèi)分解成 3389 和 2377 了。
而且這還只是舉例，3389 和 2377 這兩個數(shù)對於電腦來說已經(jīng)算是很小了。現(xiàn)行的業(yè)界標準是 RSA-2048，意思是 p 和 q 相乘以後得到的 N，大約有 2 的 2048 次方這麼大——利用高中所學(xué)的 log 位數(shù)估算法，我們可以從 2048×log 2 ≒ 616.51 得知，這個由 p 和 q 相乘得到的 N 可是一個多達 617 位數(shù)的天文數(shù)字！
以現(xiàn)在的技術(shù)而言，符合 RSA-2048 標準的 N 值是即使傾全球之力也無法短時間內(nèi)成功分解的數(shù)，因為除了把合數(shù)篩選掉（然後一個一個往上嘗試是否能夠整除）的方式以外，現(xiàn)今的數(shù)學(xué)家還沒有想到可行的方法能夠讓現(xiàn)有的經(jīng)典電腦快速地分解掉這種大型的半質(zhì)數(shù)。
當(dāng)然，這也不代表 RSA 未來不會在某個時間點被破解——也許將來量子電腦發(fā)展成熟，人類得以使用秀爾演算法快速地分解大型半質(zhì)數(shù)，又或者某個超越 RSA 發(fā)明者的怪物出現(xiàn)，突然就發(fā)明出了能夠快速分解半質(zhì)數(shù)的算法，使得金融、通訊體系的安全性一夕之間被打垮，這都不是不可能。
不過，這樣的可能性畢竟還是比較小的。即使量子電腦已經(jīng)在邁向發(fā)展成熟的路上，現(xiàn)在世界上的科學(xué)家們也正相應(yīng)地發(fā)展「基於量子電腦的量子密碼學(xué)」，我相信未來的通訊安全只會隨著時間而越來越牢固。我們平常在使用各類金融、資訊服務(wù)的同時，也別忘了這些科學(xué)家的偉大貢獻。
參閱：
維基百科相關(guān)條目：
