題目連結:
題目意譯:
給定你一個 n × n 個網(wǎng)格 grid,在其中你可以放置一些 1 × 1 × 1 的方塊。每個值 v = grid[i][j] 代表放置於 (i, j) 的方塊塔之高度。
放置完方塊後,你決定將任兩個相鄰之方塊黏在一起,形成一些不規(guī)則三維圖形。
回傳該圖形的總表面積。
注: 圖形的底部面也算在表面積裡。
限制:
n == grid.length
n == grid[i].length
1 ≦ n <= 50
0 ≦ grid[i][j] ≦ 50
範例測資:
範例 1:
輸入: grid = [[2]]
輸出: 10
範例 2:
輸入: grid = [[1,2],[3,4]]
輸出: 34
範例 3:
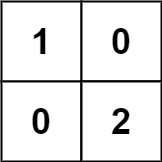
輸入: grid = [[1,0],[0,2]]
輸出: 16
範例 4:
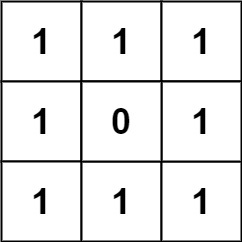
輸入: grid = [[1,1,1],[1,0,1],[1,1,1]]
輸出: 32
範例 5:
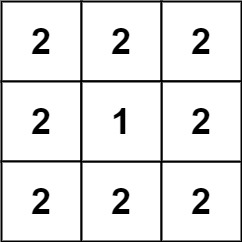
輸入: grid = [[2,2,2],[2,1,2],[2,2,2]]
輸出: 46
解題思維:
對於某座塔 grid[i][j] ,如果 grid[i][j] > 0 代表 (i, j) 有放方塊,因此一定有頂部、底部這兩個 1 × 1 之面積。
接著看這座塔的上下左右(即相鄰的塔,這邊用 G 指稱,如果 G 不存在(位置 (i, j) 位於邊緣等等),則預設為高度 0 的塔),看 grid[i][j] 與 G 之關係:
如果 grid[i][j] > G ,則代表位於 (i, j) 的這座塔會於與塔 G 相鄰的這一側露出 grid[i][j] - G 單位之面積;反之,則不會露出任何面積(因為會黏於塔 G 上)。
對於 grid 中每座塔將上述的值全數(shù)加總即是所求。
此次分享到此為止,如有任何更加簡潔的想法或是有說明不清楚之地方,也煩請各位大大撥冗討論。