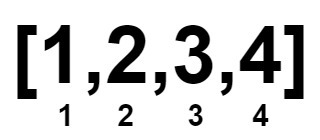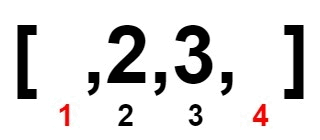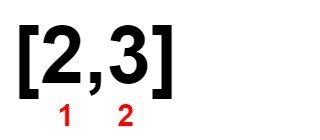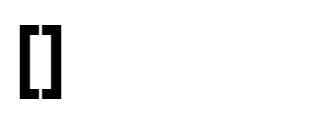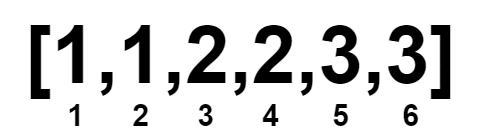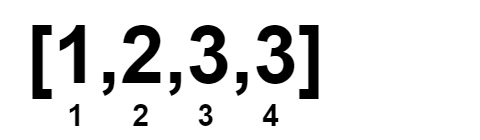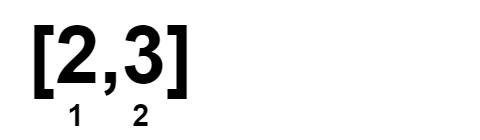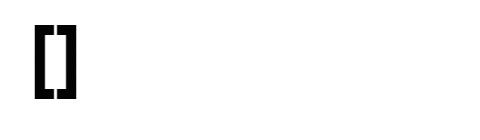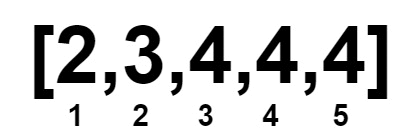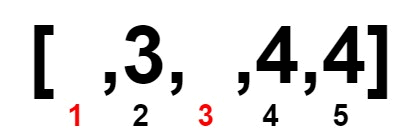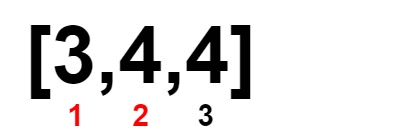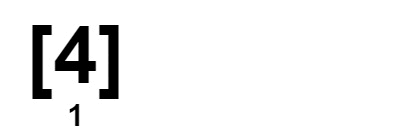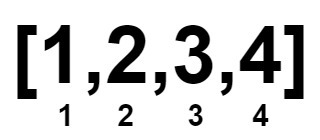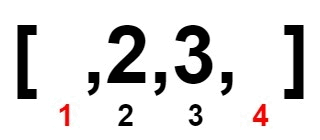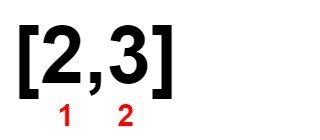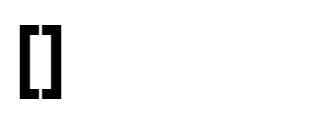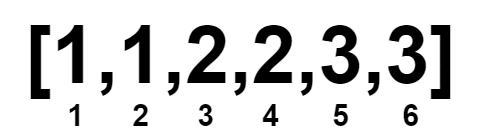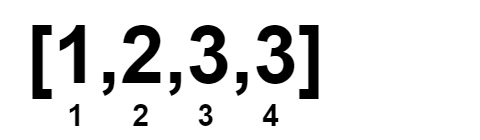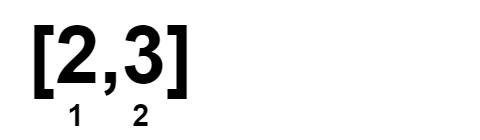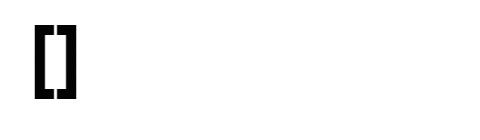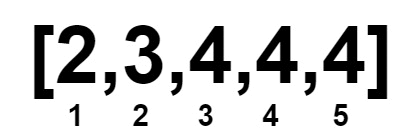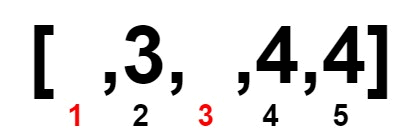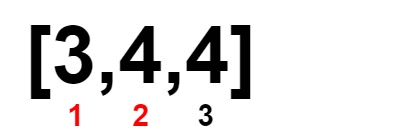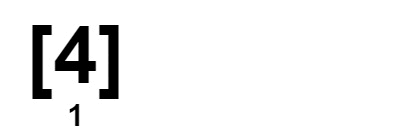題目連結:
題目意譯:
給定一個以非遞減順序排序的整數陣列 nums。
你可以執行以下操作任意次:
選擇兩個索引值 i 、 j,其中 nums[i] < nums[j]。
接著,從 nums 中位於移除索引值 i 和 j 的元素。剩餘元素將繼續維持之間的相對位置,而索引值則重新編號。
回傳執行零次或多次操作後 num 的最小長度。
限制:
1 ≦ nums.length ≦ 10 ^ 5
1 ≦ nums[i] ≦ 10 ^ 9
nums 以非遞減順序排序。
範例測資:
範例 1:
輸入: nums = [1,2,3,4]
輸出: 0
解釋:
範例 2:
輸入: nums = [1,1,2,2,3,3]
輸出: 0
解釋:
範例 3:
輸入: nums = [1000000000,1000000000]
輸出: 2
解釋:
由於兩數相同,它們將無法被移除。
範例 4:
輸入: nums = [2,3,4,4,4]
輸出: 1
解釋:
解題思維:
可以看到因為陣列已經排序了,因此題目的操作可以改寫成「挑兩個相異數字並刪除」。
很明顯地亂挑數字是不可行的。因為如果陣列中有數字佔超過一半的陣列長度,則每一次應從其餘種類的數字挑一個與該數字來刪除才能得到最小長度。
因此可以看到出現次數最多的應該要先被消掉。所以其中一種最佳策略是將兩個出現次數最多的數字各刪掉一個。然後重複這個步驟直到數字種類小於兩種為止。
但是這樣的作法時間複雜度基本上會是 O(n log n),其中 n 是 nums 的原始長度。雖然理論上可以壓到線性時間,但有沒有更單純的方式呢?
既然我們想要一個數字配另一個數字,再加上原本的陣列就已經排序好了。那麼直接把陣列切成「左半」和「右半」,然後左半和右半數字一一對齊(多的數字隨便放哪一半都行)。
因此,我們就用兩個指標 L 、 R 來分別指向左半右半各自的數字現在是什麼。
如果 L != R,則我們就刪掉這兩個數字(實際上不需要真的從陣列移除,只要統計刪掉多少數字即可),並將 L 和 R 指向下一個數字。而如果 L == R,則根據陣列原本的已經排序的特性,故 L(含)往後的數字與 R(含)往前的數字都是一樣的。因此移動 L 是沒有意義的,應當只移動 R 到下一個數字才有可能可以配對。
最後只要將陣列的長度減去刪除的數字個數即為所求最小長度。
至於為何這一定可以刪掉最多的數字,可以用反證法證明。因為這個也是一個寫起來會又臭又長的證明,故在此省略。不過還是寫一個概要給想要自己證明的讀者:簡單來說假設上面方式刪得不夠多,那麼會存在一個「多的」數對會是「統一出現在左半」、「統一出現在右半」以及「左半右半各一個數字」這三種。而可以討論這三種情況如果發生的話,要嘛直接違反陣列是排序的性質、要嘛就是本來就會被上面的演算法找到。故得證。
此次分享到此為止,如有任何更加簡潔的想法或是有說明不清楚之地方,也煩請各位大大撥冗討論。