前情提要 :
簡諧運動 (Simple Harmonic Motion) ,為一種直線型往復(fù)週期性運動。高中選修物理 (力學(xué)
一) 的部分有提到過簡諧運動這個變加速度運動,而我們以參考圓的等速圓周運動之投影來
進一步分析,求出x - t圖、v - t圖與a - t圖。
印象中某清大物理教授說參考圓的方式解簡諧運動很爛,沒有借助微分方程的運用,根本無
法直接理解簡諧運動為何是圓周運動的投影。而著名物理youtuber nash wang老師在這部分
說明,學(xué)習(xí)方向應(yīng)為發(fā)現(xiàn)等速圓周運動的投影為簡諧運動,兩者之因果關(guān)係需搞清楚。
好不管,進入正題。
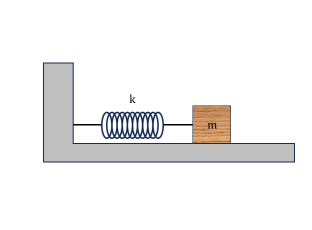
我們考慮以下系統(tǒng)的情況,如圖
一水平理想彈簧 (彈性常數(shù)為k) ,左端繫於鉛直牆面,右端繫在質(zhì)量為m的木塊上,假設(shè)木塊
和地面無摩擦阻力。此時施力向右拉動,使木塊位移A後再將其釋放。此時由能量守恆律可知
此木塊做簡諧運動的振幅為A。
需注意的是,在還未釋放時,即t = 0時,木塊的位置x(0)為A、速度v(0) = x'(0)為0。這兩條件
為微分方程的起始條件 (Initial Condition) ,等等解拉氏轉(zhuǎn)換方程時會用到。
已知滿足彈簧簡諧運動的條件為F = -kx,可得ma = -kx,即m*x''(t) = -k*x(t)。將上述式子整理
得到x''(t) + (k/m)*x(t) = 0,這是一個二階線性齊次常係數(shù)微分方程。
簡單介紹一下拉普拉斯轉(zhuǎn)換 :
又稱拉氏轉(zhuǎn)換,為一種常見的積分轉(zhuǎn)換,此積分轉(zhuǎn)換的核函數(shù)為e^(-st)。定義函數(shù) f(t) 的拉氏
轉(zhuǎn)換為L{ f(t) } = F(s) = ∫ [ 0,∞] e^(-st)*f(t) dt。
進一步衍生出L{ f '(t) } = s*F(s) - f(0) 與 L{ f ''(t) } = (s^2)*F(s) - s*f(0) - f '(0)。
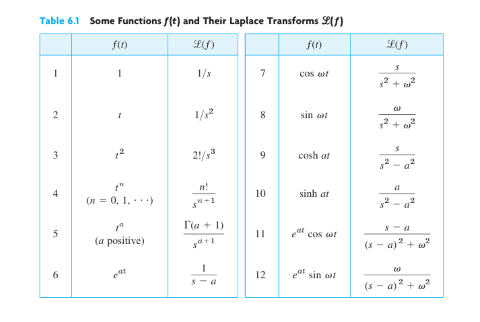
常見的拉氏轉(zhuǎn)換表如下 :
回到原來的問題,已知簡諧運動的微分方程與起始條件 :
x''(t) + (k/m)*x(t) = 0 , x(0) = A , x'(0) = 0。設(shè)x(t)的拉氏轉(zhuǎn)換為X(s),將整個等式做拉氏轉(zhuǎn)換
,即L{ x''(t) } + (k/m)*L{ x(t) } = L{ 0 } ,藉由拉氏轉(zhuǎn)換的微分性質(zhì)可得 :
(s^2)*X(s) - s*x(0) - x'(0) + (k/m)*X(s) = 0,即(s^2)*X(s) - sR + (k/m)*X(s) = 0。經(jīng)由移項得
(s^2)*X(s) + (k/m)*X(s) = sR,X(s) = R*( s/((s^2) + (k/m)) )
最後再將X(s)做反拉轉(zhuǎn)換即可得到x(t)。
依照上圖的拉氏轉(zhuǎn)換,可得x(t) = R*cos(√(k/m)t)
基本上在學(xué)物理數(shù)學(xué)時,解這類型的微分方程都以假設(shè)x(t) = e^(λt)找齊次解。本文以常見的
手拉彈簧自由釋放的情況,利用具有起始條件的特性選擇用拉氏轉(zhuǎn)換的方式解題。找出科學(xué)
問題的解決方法本來就不限於一種 !
參考資料 : { Advanced Engineering Mathematics } (10th , Erwin Kreyszig )