題目連結(jié):
題目意譯:
給定一個(gè)矩形狀的披薩,其以一個(gè)大小為 rows × cols 的矩陣所表示,其矩陣包含以下字元:'A'(一顆蘋(píng)果)和 '.'(空格)。同時(shí)你也被給定一整數(shù) k。你需要對(duì)披薩切 k - 1 刀來(lái)將它分成 k 塊。
對(duì)於每一刀,你將先選擇方向:垂直或是水平;接著你將選擇位於格子邊界作為下刀的位置並接著將披薩切成兩塊。如果你是垂直地縱切披薩,則把切完後左邊的部分給某個(gè)人;而如果你是水平地橫切披薩,則把切完後上面的部分給某個(gè)人。而最後一塊披薩則給最後一個(gè)人。
回傳所有可能的披薩切割方法數(shù),使得切法中每一塊至少包含一顆蘋(píng)果。由於答案可能很大,將其模 10 ^ 9 + 7 後再回傳。
限制:
1 ≦ rows, cols ≦ 50
rows == pizza.length
cols == pizza[i].length
1 ≦ k ≦ 10
pizza 只由字元 'A' 和 '.' 所組成。
範(fàn)例測(cè)資:
範(fàn)例 1:
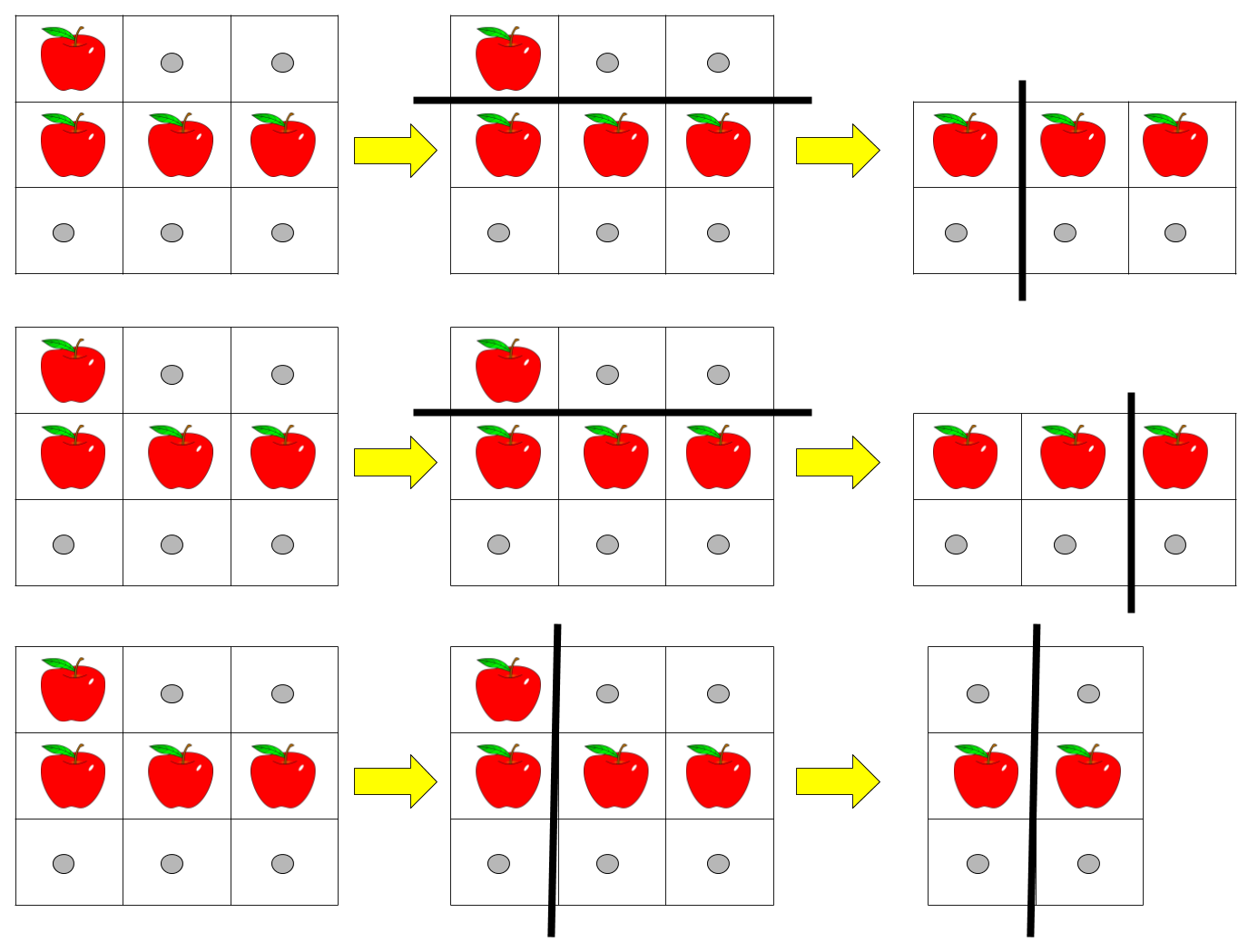
輸入: pizza = ["A..","AAA","..."], k = 3
輸出: 3
解釋: 上圖顯示了三種切披薩的方式。注意到每一塊之中必須包含至少一顆蘋(píng)果。
範(fàn)例 2:
輸入: pizza = ["A..","AA.","..."], k = 3
輸出: 1
範(fàn)例 3:
輸入: pizza = ["A..","A..","..."], k = 1
輸出: 1
解題思維:
首先先利用
這題的想法建立出二維前綴和(Prefix Sums),讓我們可以在常數(shù)時(shí)間內(nèi)得到矩陣 pizza 中任一個(gè)子矩陣內(nèi)的蘋(píng)果數(shù)量。
接下來(lái)就是經(jīng)典的動(dòng)態(tài)規(guī)劃(Dynamic Programming,DP)之題型:
定義一個(gè)三維矩陣 D,其中 D[r][c][x] 代表著以矩陣 pizz 中以左上角 (r, c) 且右下角 (rows - 1, cols - 1) 的這個(gè)子矩陣來(lái)說(shuō),在需要切 x 刀的情況下,符合題目的切法之方法數(shù)。
因此我們可以看到其遞迴式為:
如果 D[r][c][x] 代表著子矩陣中沒(méi)有蘋(píng)果(利用一開(kāi)始建立的前綴和來(lái)算),則 D[r][c][x] = 0;
如果 x 為 0,則代表只有現(xiàn)在「一種切法」,即維持原狀,因此 D[r][c][x] = 1;
如果 r 為 rows - 1 、 c 為 cols - 1 且 x 不為 0,則代表剩下沒(méi)辦法再切了,因此 D[r][c][x] = 0;
如果以上皆非,則 D[r][c][x] = D[i + 1][c][x - 1] + D[r][j + 1][x - 1],對(duì)於所有滿足 r ≦ i < rows - 1 的 i 值且左上角 (r, c) 而右下角為 (i, cols - 1) 的子矩陣要有蘋(píng)果;以及所有滿足 c ≦ j < cols - 1 的 j 值且左上角 (r, c) 而右下角為 (rows - 1, j) 的子矩陣要有蘋(píng)果。
因此我們利用深度優(yōu)先搜尋(Depth First Search,DFS)的精神 + 記錄已經(jīng)求過(guò)的答案去遞迴求得 D[0][0][k - 1] 之值,最後便可以得到所求。
此次分享到此為止,如有任何更加簡(jiǎn)潔的想法或是有說(shuō)明不清楚之地方,也煩請(qǐng)各位大大撥冗討論。