題目連結:
題目意譯:
一個矩陣對角線為一條由多個格子組成的對角線,其從某個最上面的列或最左邊的行開始,按照右下方向前進直到碰到矩陣的邊緣為止。例如說,從 mat[2][0] 這個位置開始的矩陣對角線,其中 mat 為一個 6 × 3 大小之矩陣,將包含格子 mat[2][0] 、 mat[3][1] 、 mat[4][2]。
(譯者注:也就是說矩陣左上角是第 0 列第 0 行)
給定一格 m × n 大小的整數矩陣 mat,將每個矩陣對角線按照數值升序來排序,並回傳結果矩陣。
限制:
m == mat.length
n == mat[i].length
1 ≦ m, n ≦ 100
1 ≦ mat[i][j] ≦ 100
範例測資:
範例 1:
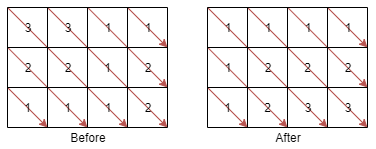
輸入: mat = [[3,3,1,1],[2,2,1,2],[1,1,1,2]]
輸出: [[1,1,1,1],[1,2,2,2],[1,2,3,3]]
範例 2:
輸入: mat = [[11,25,66,1,69,7],[23,55,17,45,15,52],[75,31,36,44,58,8],[22,27,33,25,68,4],[84,28,14,11,5,50]]
輸出: [[5,17,4,1,52,7],[11,11,25,45,8,69],[14,23,25,44,58,15],[22,27,31,36,50,66],[84,28,75,33,55,68]]
解題思維:
直接窮舉矩陣對角線可能開始的位置,然後對於每個位置開始往右下跑到底會得到一個數列。將該數列排序後放回原位(即剛剛掃過的順序)。
這樣一來,便可以把所有對角線上的元素各自排序。
此次分享到此為止,如有任何更加簡潔的想法或是有說明不清楚之地方,也煩請各位大大撥冗討論。