題目連結(jié):
題目意譯:
在一條長長的圖書館走廊上,那裡有著一排座位以及盆景植物。你被給定一個索引值從 0 開始的、長度為 n 的字串 corridor,其由字母 'S' 和 'P' 所組成。其中每個 'S' 代表著一個座位且每個 'P' 代表著一盆植物。
一個房間間隔已經(jīng)安裝在索引值 0 的左側(cè),而另一個則安裝在索引值 n - 1 的右側(cè)。而我們可以安裝額外的房間間隔。對於每個介於索引值 i - 1 和 i 之間(1 ≦ i ≦ n - 1)的位置,最多一個房間間隔可以安裝於其中。
請將走廊間隔成多個不重疊的區(qū)域,其中每個區(qū)域擁有恰好兩個座位以及任意數(shù)量的植物。間隔方式可能有很多種。如果存在某個位置使得在第一種方式下是有安裝房間間隔的而另一種方式則無安裝,則此兩個方式視為相異。
回傳將走廊間隔開的方法數(shù)。由於答案可能很大,將其模 10 ^ 9 + 7 後再回傳。如果不存在任何方式,則回傳 0。
限制:
n == corridor.length
1 ≦ n ≦ 10 ^ 5
corridor[i] 只會是 'S' 或是 'P'。
範例測資:
範例 1:
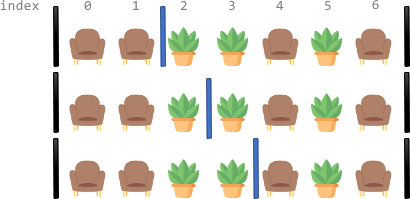
輸入: corridor = "SSPPSPS"
輸出: 3
解釋: 有三個不同的方式可以分隔走廊:
上圖中的黑條代表著兩個先前已經(jīng)安裝的房間間隔。
注意到每種方式中,每個區(qū)域都有恰好兩個座位。
範例 2:
輸入: corridor = "PPSPSP"
輸出: 1
解釋: 只有一種方式可以分割走廊,也就是完全不裝設(shè)額外的間隔。
安裝任何一個間隔將會使得某些區(qū)域沒有恰好兩個座位。
範例 3:
輸入: corridor = "S"
輸出: 0
解釋: 沒有任何方式可以分割走廊,因為一定有一區(qū)域沒有恰好兩個座位。
解題思維:
首先,可以看到?jīng)]有任何座位或是奇數(shù)個座位的分割方法數(shù)必定是 0。因為將會有區(qū)域出現(xiàn)未恰好滿兩個座位的情況出現(xiàn)。
接著,可以看到在任何一種方式下位於同一區(qū)域的兩個座位,在其他分割方式下也同樣會位於同一區(qū)域。如同範例一中索引值 0 和 1 那兩個座位,或是索引值 4 和 6 那兩個座位。這兩對座位不管在哪個方式下都是成對的(因此,每對座位之間的植物也會位於同一區(qū)域)。
因此,我們可以先掃過一次 corridor 這個字串,然後將這些座位配對先找出來(方法很簡單,就是每次數(shù)滿兩個座位就可以成對了)。所以整個 corridor 可以改寫成
PP……OPP……OPP………………OP……P
其中 P 一樣是代表著盆景植物,而 O 則代表成對的座位(以及兩個座位中間夾著的植物們)。
此時可以看到因為第一個 O 的左側(cè)沒有其他的 O 存在了,因此其左側(cè)的植物們(如果有的話)也必定會與其位於同一區(qū)域內(nèi)。同理,最右側(cè)的那一群植物也會與最後一個 O 位於同一區(qū)域。而其餘的植物便可以選擇要分於哪一側(cè)。
例如現(xiàn)在兩個 O 之間有著 x 盆植物,則我們可以把
0 盆植物分在左側(cè)的 O、x 盆分在右側(cè)的 O;或把
1 盆植物分在左側(cè)的 O、x - 1 盆分在右側(cè)的 O;或把
2 盆植物分在左側(cè)的 O、x - 2 盆分在右側(cè)的 O;或把
……
x - 1 盆植物分在左側(cè)的 O、1 盆分在右側(cè)的 O;或把
x 盆植物分在左側(cè)的 O、0 盆分在右側(cè)的 O。
總計會有 x + 1 種分法。
而每兩個 O 之間都可以算出這樣的數(shù)值,稱其為 c1 、 c2 、 c3、……則所求方法數(shù)實際上就是
c1 × c2 × c3 × ……
不過記得在計算過程中取 10 ^ 9 + 7 的餘數(shù),以免溢位。
此次分享到此為止,如有任何更加簡潔的想法或是有說明不清楚之地方,也煩請各位大大撥冗討論。