題目連結:
題目意譯:
你被給定兩整數 n 和 m 以及兩個整數陣列 hBars 和 vBars。有一個網格有著 n + 2 條水平線以及 m + 2 條鉛直線,隔出了若干個大小為 1 × 1 的格子。這些線的索引值從 1 開始數。
你可以從 hBars 中移除若干條對應索引值的水平線,以及從 vBars 中移除若干條對應索引值的鉛直線。注意到其他沒有存在於 hBars 或 vBars 中的線不得被移除。
回傳一個整數代表著網格中可以藉由移除某些線(可以都不移除)來得到一個方形「洞」之最大面積值。
限制:
1 ≦ n ≦ 10 ^ 9
1 ≦ m ≦ 10 ^ 9
1 ≦ hBars.length ≦ 100
2 ≦ hBars[i] ≦ n + 1
1 ≦ vBars.length ≦ 100
2 ≦ vBars[i] ≦ m + 1
hBars 中所有數值彼此相異。
vBars 中所有數值彼此相異。
範例測資:
範例 1:
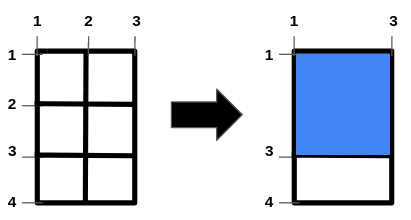
輸入: n = 2, m = 1, hBars = [2,3], vBars = [2]
輸出: 4
解釋:
左圖代表著一開始由各條線組成的網格。水平線為 [1,2,3,4] 而鉛直線為 [1,2,3]。
其中一種得到最大面積的方形洞之方式為移除水平線 2 以及鉛直線 2。
範例 2:
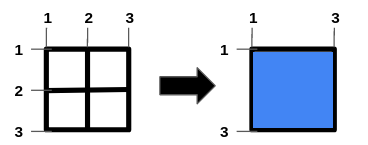
輸入: n = 1, m = 1, hBars = [2], vBars = [2]
輸出: 4
解釋:
為了得到最大面積的方形洞,我們移除掉水平線 2 和鉛直線 2。
範例 3:
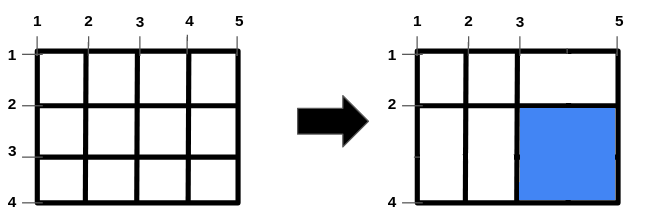
輸入: n = 2, m = 3, hBars = [2,3], vBars = [2,4]
輸出: 4
解釋:
其中一種得到最大面積的方形洞之方式為移除水平線 3 以及鉛直線 4。
解題思維:
首先,將 vBars 和 hBars 各自由小排到大。
為了最大化「洞」的面積,我們需要盡可能地將邊長變長。而我們可以看到,當有若干條同方向的線之編號是連續的時候(例如說 vBars 中有編號 2 、 3 、 4 、 5 這 4 條連續的線等等),則我們可以藉由移除這幾條線來得到邊長等於「連續編號的長度 + 2」之邊長。
因此我們可以掃過 vBars 和 hBars 各自找出最長的連續編號連號之片段,假設前者是 V、後者是 H。則洞最大的面積值即為
(min(V, H) + 2) ^ 2
此次分享到此為止,如有任何更加簡潔的想法或是有說明不清楚之地方,也煩請各位大大撥冗討論。