題目連結:
題目意譯:
你被給定一個整數 n 以及一個索引值從 0 開始數的二維陣列 queries,其中 queries[i] = [typei, indexi, vali]。
一開始,現在有一個索引值從 0 開始數的 n × n 矩陣填滿了 0。對於每一筆詢問,你需要執行以下更新之一:
如果 typei == 0,將索引值 indexi 那一列的數字設為 vali,覆蓋掉前面寫入過的數字。
如果 typei == 1,將索引值 indexi 那一行的數字設為 vali,覆蓋掉前面寫入過的數字。
回傳所有詢問執行完之後矩陣中所有整數之總和。
限制:
1 ≦ n ≦ 10 ^ 4
1 ≦ queries.length ≦ 5 × 10 ^ 4
queries[i].length == 3
0 ≦ typei ≦ 1
0 ≦ indexi < n
0 ≦ vali ≦ 10 ^ 5
範例測資:
範例 1:
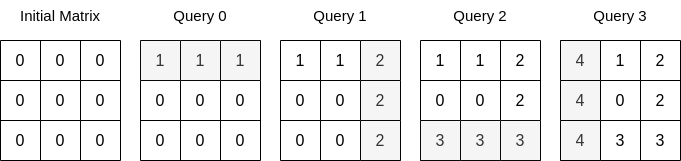
輸入: n = 3, queries = [[0,0,1],[1,2,2],[0,2,3],[1,0,4]]
輸出: 23
解釋: 上圖顯示了每一筆詢問後的矩陣。所有詢問執行完之後矩陣中所有整數之總和為 23。
範例 2:
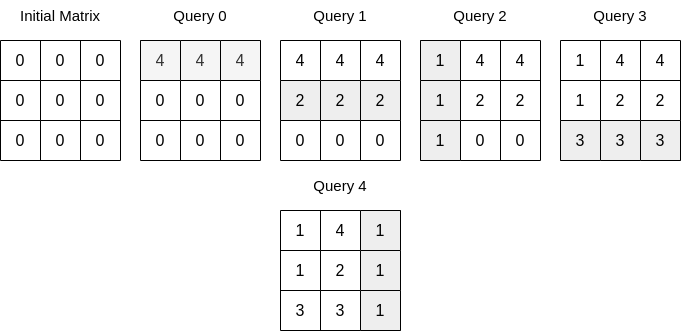
輸入: n = 3, queries = [[0,0,4],[0,1,2],[1,0,1],[0,2,3],[1,2,1]]
輸出: 17
解釋: 上圖顯示了每一筆詢問後的矩陣。所有詢問執行完之後矩陣中所有整數之總和為 17。
解題思維:
(令 q = queries.length)
可以看到最後一筆詢問將會是為整個矩陣的總和貢獻 queries[q - 1][2] × n 之值。而發生在 queries[q - 1] 之前都任何數值修改都改變不了該筆詢問所寫下的數值(畢竟其為最晚發生者)。
因此我們可以視為將該筆詢問所更新的那一行(或列。取決於該詢問的 typei 之值)被「抹除」掉了。例如說,如果 queries[q - 1] 修改的是某一列的數值,而 queries[q - 2] 則是修改某一行的值。則 queries[q - 2] 實際上最後只會更新到 n - 1 列的數值,因此貢獻了總和中的 queries[q - 2] × (n - 1)。
而其他情況以此類推。因此我們可以藉由反著掃過陣列 queries,並維護當前尚未被「抹除」的列數以及行數來為每一筆詢問計算其最終貢獻總和值。全數加總後即為所求。
此次分享到此為止,如有任何更加簡潔的想法或是有說明不清楚之地方,也煩請各位大大撥冗討論。