題目連結:
題目意譯:
現在有一個有向加權圖,其由編號依序為 0 到 n - 1 的 n 個節點所組成。圖中的邊一開始是以一個給定的陣列 edges 所表示,其中 edges[i] = [fromi, toi, edgeCosti] 代表著有一條邊是從 fromi 走到 toi 且成本為 edgeCosti。
實作類別 Graph:
Graph(int n, int[][] edges) 初始化一個物件,其有著 n 個節點以及給定的邊。
addEdge(int[] edge) 新增一條邊到 edges 中,其中 edge = [from, to, edgeCost]。保證在加入此邊之前,from 和 to 兩個節點之間無邊存在。
int shortestPath(int node1, int node2) 回傳從 node1 走到 node2 的路徑之最小成本值。如果不存在著這樣子的路徑,則回傳 -1。一條路徑的成本為路徑上的邊之成本總和。
限制:
1 ≦ n ≦ 100
0 ≦ edges.length ≦ n × (n - 1)
edges[i].length == edge.length == 3
0 ≦ fromi, toi, from, to, node1, node2 ≦ n - 1
1 ≦ edgeCosti, edgeCost ≦ 10 ^ 6
在任何時刻,圖中都不會有重邊以及自環存在。
最多呼叫 addEdge 100 次。
最多呼叫 shortestPath 100 次。
範例測資:
範例 1:
輸入
["Graph", "shortestPath", "shortestPath", "addEdge", "shortestPath"]
[[4, [[0, 2, 5], [0, 1, 2], [1, 2, 1], [3, 0, 3]]], [3, 2], [0, 3], [[1, 3, 4]], [0, 3]]
輸出
[null, 6, -1, null, 6]
解釋
Graph g = new Graph(4, [[0, 2, 5], [0, 1, 2], [1, 2, 1], [3, 0, 3]]);
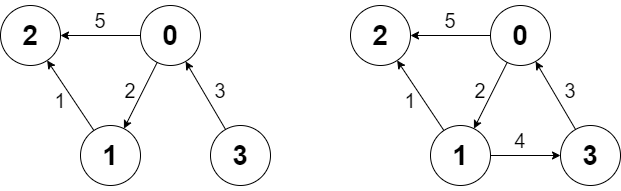
g.shortestPath(3, 2); // 回傳 6。在上圖中的第一個圖形裡,從 3 走到 2 的最短路徑為 3 -> 0 -> 1 -> 2,其總成本為 3 + 2 + 1 = 6。
g.shortestPath(0, 3); // 回傳 -1。因為不存在任何路徑從 0 走到 3。
g.addEdge([1, 3, 4]); // 我們在節點 1 和節點 3 之間新增了一條邊,而此時我們得到了上圖中的第二個圖形。
g.shortestPath(0, 3); // 回傳 6。0 走到 3 的最短路徑現在變成了 0 -> 1 -> 3,其總成本為 2 + 4 = 6。
解題思維:
由於 addEdge 只會被呼叫最多 100 次且總節點數最多也只有 100 個,所以我們可以使用 Floyd-Warshall(參見
這題)來動態地維護所有可能節點對之間的最短路徑。
初始化沒什麼特別的,就是單純地先跑一次 Floyd-Warshall 來計算出當前所有節點對的最短路徑。
呼叫 shortestPath 的時候也沒什麼問題,就是單純地存取儲存在二維陣列中的 node1 到 node2 之最短距離(下面沿用上述提及的文章中之符號,故此邊可寫為 d[node1][node2])即可。
呼叫 addEdge 時,可以看到如果 edgeCost ≧ d[from][to] 的話,不需要更新任何點對之間的最短距離;反之,則可以觀察得到如果 edgeCost 會影響其他節點對 (i, j) 的最短距離的話,則代表著 d[i][j] > d[i][from] + edgeCost + d[to][j]。也就是說,要影響 (i, j) 的答案意味著他們將必定走到從 from 到 to 的這條邊。由於不知道實際上會影響哪些節點對,因此需要窮舉所有可能的 (i, j)。
所以可以看到單次呼叫的時間複雜度為以下:
初始化:O(n ^ 3)
addEdge:O(n ^ 2)
shortestPath:O(1)
因此總體時間複雜度為 O(n ^ 3 + x × n ^ 2 + y),其中 x 、 y 為分別呼叫 shortestPath 和 addEdge 的次數。
此次分享到此為止,如有任何更加簡潔的想法或是有說明不清楚之地方,也煩請各位大大撥冗討論。