這學期上課學到的好玩東西
Range Minimum Query (RMQ):
給定 N 個數字,以及 Q 筆查詢,
每個查詢 L, R 回傳 [L, R] 中最?。╫r 最大)的數字。
常見資料結構:
線段樹:
很通用的資料結構,可以拿來解很多問題,O(N logN) 前處理,每次查詢 O(log N)。
但還不夠 Optimal!
Sparse Table:
對每個 index i,紀錄 [i, i + 2^j] 中的 RMQ, j 的範圍從 0 到 lg(N),前處理 O(N logN),每次查詢 O(1)。
雖然 O(1) 查詢很香,但 O(N logN) 前處理好長...
Cartesian Tree:
可以將 RMQ 問題轉為 LCA 問題,O(N) 建表,查詢要看設計方法。
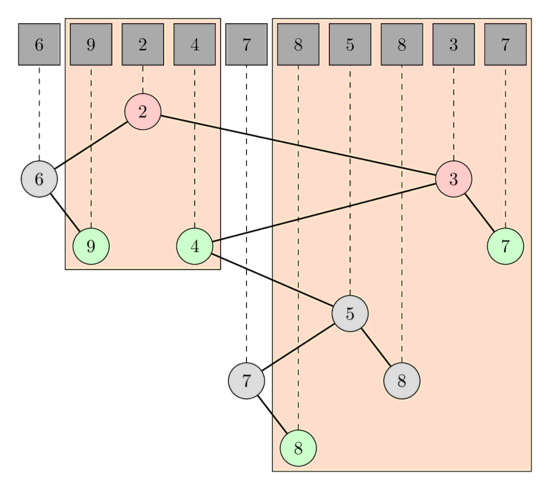
若要把整條陣列打成一棵樹,那窮舉左右端點算 LCA 至少也要 O(N^2),所以要想個更好的方法來降低複雜度。
不如就分塊吧!
如果把每 s = 0.5 * logN 個數字當成一塊,然後把他們各自打成一棵笛卡爾樹,再對同樣形狀的樹窮舉左右端點找 RMQ,這樣會變成
O(s^2) 窮舉左右端點 * O(2^s) 可能出現的樹的形狀的數量 = O(log^2 N) * O(N^0.5) = O(N) 建表!
因為透過陣列本身和已算好的 RMQ,可以在 O(1) 內找到往右多包一個數字的 RMQ,所以上面 O(N) 建表是真的可行。
至於跨區塊的 query ,我們可以先將每棵樹的最小元素記起來,做成 Sparse table,這樣總共 M=N/s 個樹,然後上面提到的 Sparse table 複雜度是 O(N logN) 建表,再把 N 換成 M,變成了
O(M logM) = O(N / logN) * O(log(N / logN) ) = O(N / logN) * O(logN - loglogN) = O(N) 建表!
綜合以上,可以將 RMQ 問題變成 O(N) 建表和 O(1) 查詢。
Optimal RMQ:
對於輸入有 N 個元素的陣列,先將其轉換為區塊長度(S)的整數倍,多的補 inf 就好了,不會影響結果。
再來記錄笛卡爾樹,並將其轉換為一個可逆的編碼,我這邊是用 DFS,若一個 node 有左節點,那將 encode |= 2,若有右節點,則 encode |= 1。
建好一棵樹之後,若與他形狀相同的樹,還沒建過樹裡面的 RMQ table,就要對他建一次表。
最後就要建區塊之間的 Sparse Table 了!
在前處理的最後一部分,把全部捏在一起。
前處理完成!
對於查詢,可以先檢查左右 index 各處於哪一個 block,分成兩個 case:
若在同一個區塊中,則找目前這個 block 中 [L % s, R % s] 的 RMQ,直接回傳就好。
若不在同個區塊,那可以把答案分成三個部分:中間跨越的區塊 + 左邊剩下的部分 + 右邊剩下的部分。
這也很簡單,中間的查 Sparse table,左右的都查對應的樹中,那一個區塊的 RMQ,最後再回傳最小值。
這樣就完成了!
裡面取 s = 9,是直接對題目的輸入大小上限,算 0.5log(N) 的近似,比較懶。