題目連結(jié):
題目意譯:
你被給定一個(gè)大小為 m × n 的二元矩陣 grid。
「一步」是由選定任意列或任意行並將該列或該行上的數(shù)字變換(即,將所有 0 變 1 、所有 1 變 0)。
矩陣中的每一列將會(huì)被詮釋為一個(gè)二進(jìn)位數(shù)字,而該矩陣的分?jǐn)?shù)為這些數(shù)字之加總。
回傳若干步(可以為零步)後可以得到的最大分?jǐn)?shù)值。
限制:
m == grid.length
n == grid[i].length
1 ≦ m, n ≦ 20
grid[i][j] 只會(huì)是 0 或是 1。
範(fàn)例測(cè)資:
範(fàn)例 1:
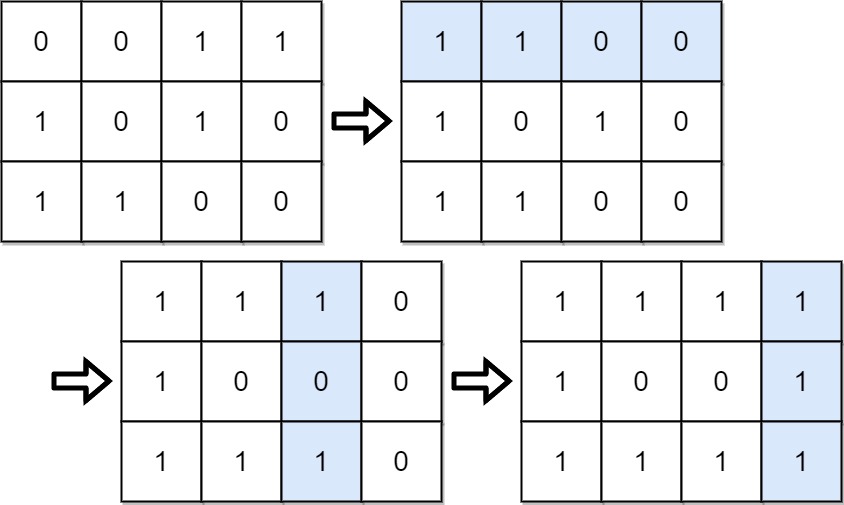
輸入: grid = [[0,0,1,1],[1,0,1,0],[1,1,0,0]]
輸出: 39
解釋: 0b1111 + 0b1001 + 0b1111 = 15 + 9 + 15 = 39
範(fàn)例 2:
輸入: grid = [[0]]
輸出: 1
解題思維:
可以看到藉由先選定列來(lái)變換數(shù)字使得每一列的開頭都是 1,必定是最佳策略。
用反證法證明即可:
假設(shè)存在某個(gè)最佳解使得某幾列不是 1 開頭。則對(duì)於單一一個(gè)不是 1 開頭的列而言,無(wú)論開頭後面長(zhǎng)怎樣最後的加總必定小於以 1 開頭的數(shù)字(以十進(jìn)位來(lái)舉例的話就是 00000 ~ 09999 無(wú)論如果就是比不過(guò) 10000;二進(jìn)位也同理)。
因此每一個(gè)不是以 1 開頭的列都可以換成更大的數(shù)字。因此我們可以得到一個(gè)總和比假設(shè)的最佳解更大的解。故矛盾。
所以命題成立。
所以我們可以先將若干列翻轉(zhuǎn)變成 1 開頭。而接著只需要考慮行的變換即可。而變換條件也很簡(jiǎn)單,只要該行上的 0 之?dāng)?shù)量大過(guò) 1 之?dāng)?shù)量,即變換該行。
最後將每一列作為二進(jìn)位數(shù)字加總即可得到所求。
此次分享到此為止,如有任何更加簡(jiǎn)潔的想法或是有說(shuō)明不清楚之地方,也煩請(qǐng)各位大大撥冗討論。