題目連結:
題目意譯:
給定一個大小為 n × n 的矩陣 grid,回傳有著「非零位移量」的「掉落路徑」之最小總和值。
Given an n x n integer matrix grid, return the minimum sum of a falling path with non-zero shifts.
一個有著「非零位移量」的「掉落路徑」為從 grid 中每一列選出恰好一個元素,並且每兩個相鄰列選定的元素不在同一行上。
限制:
n == grid.length == grid[i].length
1 ≦ n ≦ 200
-99 ≦ grid[i][j] ≦ 99
範例測資:
範例 1:
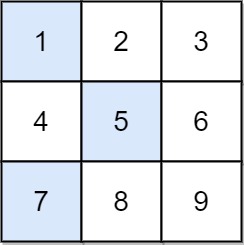
輸入: grid = [[1,2,3],[4,5,6],[7,8,9]]
輸出: 13
解釋:
可能的掉落路徑為
[1,5,9] 、 [1,5,7] 、 [1,6,7] 、 [1,6,8] 、
[2,4,8] 、 [2,4,9] 、 [2,6,7] 、 [2,6,8] 、
[3,4,8] 、 [3,4,9] 、 [3,5,7] 、 [3,5,9]
有著最小總和的掉落路徑為 [1,5,7],所以答案為 13。
範例 2:
輸入: grid = [[7]]
輸出: 7
解題思維:
基本上與
系列第一題一致。只是現在從 (r, c) 這個位置可以走到除了 (r + 1, c) 以外的 (r + 1, 0) 、 (r + 1, 1) 、 …… 、 (r + 1, n - 1) 的位置。
此次分享到此為止,如有任何更加簡潔的想法或是有說明不清楚之地方,也煩請各位大大撥冗討論。